Математическое моделирование в естественных науках

В нашей постановке происходят фазовые переходы, которые необходимо учесть. Для этого в работе [4] были введены силы, действующие между веществом в соседних узлах решетки:

Gk < 0 отталкиванию соответственно. Необходимо отметить, что на квадратной сетке (D2Q9) сила взаимодействия между узлами по диагонали в 4 раза меньше, чем сила между ближайшими соседями, т.е. G1−4 = G0 , а G5−8 = G0 / 4 . При введении такого взаимодействия состояние среды принимает вид:

где α – коэффициент, зависящий от вида решетки. Для D2Q9

α= 1,5 . Из уравнения (3) выражается «эффективная плотность».

Вработе [5] была предложена конечно-разностная формула, обеспечивающая достаточную изотропность для двумерной модели D2Q9:

использовалось уравнение Ван-дер-Ваальса в приведенных пе-

391

пользуемого уравнения состояния и был принят равным 0,152.

Моделирование процесса осаждения частиц на поверхность изделия

На рисунке представлен пример моделирования процесса конденсации частиц на твердую поверхность из газовой фазы, получаемой путем испарения жидкой капли в замкнутой камере. С течением времени под действием сил межмолекулярного

t = 10 000 t = 12 500 t = 12 600

Рис. Эволюция осаждения покрытия. Сетка: 200x200. Шкала плотности: белый цвет – (ρ = 0) и красный

цвет ρ = 1,5, T~ = 0,8, τ = 0,9

392

взаимодействия происходит конденсация газа в жидкую фазу на поверхности изделия, расположенного на правой стенке камеры. В момент времени t = 12 600 распыленное вещество мишени полностью сконденсировалось на изделии.

Заключение

Метод решеточных уравнений Больцмана успешно реализован для задач осаждения частиц из газовой фазы на твердую поверхность изделия.

Список литературы

1.McNamara G.R., Zanetti G. Use of the Boltzmann equation to simulate lattice-gas automata // Phys. Rev. Lett. – 1988. – Vol. 61,

№20. – P. 2332–2335.

2.Higuera F.J., Jimenez J. Boltzmann approach to lattice gas simulations // Europhys. Lett. – 1989. – Vol. 9, № 7. – P. 663–668.

3.Bhatnagar P.L., Gross. E.P., Krook M.K. A model for collision process in gases. I. Small amplitude process in charged and neutral one-component system // Phys. Rev. – 1954. – Vol. 94, № 3. – P. 511–525.

4.Shan X., Chen H. Lattice Boltzmann model for simulating flows with multiple phases and components // Phys. Rev. – 1993. – Vol. 47, № 3. – P. 1815–1819.

5.Куперштох А.Л. Моделирование течений с границами раздела фаз жидкость–пар методом решеточных уравнений Больцмана // Вестник Новосиб. гос. ун-та. Сер.: Математика, механика и информатика. – 2005. – Т. 5, № 3. – С. 29–42.

393

МОДЕЛЬ ОБРАЗОВАНИЯ НАНОСТРУКТУР В РЕЛЬСОВОЙ СТАЛИ ПРИ ДЛИТЕЛЬНОЙ ЭКСПЛУАТАЦИИ

В.Д. Сарычев, С.А. Невский, С.В. Коновалов, А.Ю. Грановский

(Сибирский государственный индустриальный университет, Новокузнецк, Россия, snevskiy@bk.ru)

Предложена математическая модель формирования наноструктур в рельсовой стали при длительной эксплуатации в тяжелонагруженных условиях. Она основана на представлении о том, что при интенсивной пластической деформации между слоями материала возникает неустойчивость Кельвина–Гельмгольца, которая приводит к образованию данных структур.

Ключевые слова: неустойчивость Кельвина–Гельмгольца, наноструктуры, дисперсионное уравнение, волновое число.

Известно, что различные внешние воздействия на материалы существенно изменяет их структуру и механические свойства. В качестве примера можно привести изнашивание рельсов в процессе их эксплуатации. В работах [1, 2] выявлено, что интенсивное изнашивание рельсовой стали приводит к образованию «белого слоя». Электронно-микроскопическое исследование этого слоя показало, что он состоит из зерен с размерами от 15 до 500 нм. Образование наноструктур, по мнению авторов [2], является результатом превращений в твердом теле, аналогичным механическому легированию. С другой стороны, как показывают результаты работ [3, 4], в условиях трения скольжения также возникают наноструктуры. Механизм их возникновения, по мнению авторов [3, 4], заключается в том, что под действием силы трения происходит перемещение всего поверхностного слоя материала вдоль направления скольжения. Его движение можно сравнить с ламинарным течением вязкой жидкости, скорость которого неодинакова по сечению потока. Следовательно, в различные моменты времени на различной глубине, на границах упругих и пластически деформированных

394

областей и внутри зон интенсивного пластического сдвига существуют поверхности тангенциального разрыва скорости.

С точки зрения гидродинамики на таких поверхностях имеет место абсолютная неустойчивость, представляющая собой простейший случай неустойчивости Кельвина–Гельмголь- ца – абсолютную неустойчивость специального типа поверхностей раздела, отделяющих друг от друга области течения, заполненные одной и той же или разными жидкостями, движущимися с разной скоростью. Еще одна поверхность, на которой имеет место неустойчивость Кельвина–Гельмгольца, – граница между поверхностным слоем и упругодеформированным основным материалом. Для количественной оценки перехода к турбулентному течению в [3, 4] использовался критерий Рейнольдса. Число Рейнольдса, найденное в [4] из данных по скорости движения и толщины поверхностного слоя, имеет значение от 900 до 30 000. При таких значениях плоскопараллельное течение становится неустойчивым, т.е. любое малое возмущение приводит к возникновению турбулентности. Данные оптической, атомно-силовой микроскопии и СЭМ анализа показали, что

вматериале присутствуют зоны неустойчивого течения материала, имеющие вихреобразную форму. Следует отметить, что теория Рейнольдса справедлива только для бесконечно малых возмущений, в то время как сама структура поликристаллического материала уже предполагает неоднородность его свойств, а условия трения – неоднородность механического и термического воздействия. В таком случае пластическое течение также может быть неоднородным. Расчеты трения скольжения с использованием одномерной макроскопической модели, выполненные для медного образца, показали, что пластический сдвиг

вповерхностном слое развивается нестационарно во времени

инеоднородно по глубине [6]. Таким образом, следует заключить, что в поверхностном слое каждый момент времени должно существовать несколько поверхностей, на которых возможно

395

образование турбулентности. Следовательно, гидродинамический подход дает адекватное качественное объяснение формированию наноструктур при трении.

Следует отметить, что детальной модели формирования слоев, которая связывала бы параметры материалов с характером внешнего воздействия, предложено не было. Поэтому целью нашей работы является выявление параметров материала и воздействий для формирования нанослоев в рельсах при длительной эксплуатации. Модель образования таких структур при воздействии концентрированных потоков энергии предложена в [5]. В этой работе найдено два максимума инкремента неустойчивости, причем один из них приходится на нанометровый диапазон. Наличие этого слоя обусловлено вязкостью.

ρ2, имеющая в стационарном состоянии постоянную скорость u0 , направленную вдоль оси x. Возмущение границы раздела имеет вид: η= η0 exp(ωt − ikx), где ω= α+ iΩ – комплексная ча-

стота, α – декремент, Ω – частота, k – волновое число. В работе [6] получено следующее дисперсионное уравнение:

(2νk2 + ω)2 + μ(ω+ iku0 )2 + ω02 =

396

Проанализируем зависимость параметра С от волнового числа. Нули этой функции расположены в точках

k1,2 = kmC0 (1± 1−1/ C02 ). Если значения k < k1 и k > k2, то C > 0, и в этом случае:

чивость в нанодиапазоне будет наблюдаться при k2 > k0. Это условие дает ограничение на С0, при котором значение декремента будет положительным 2С0 < 1 или

397

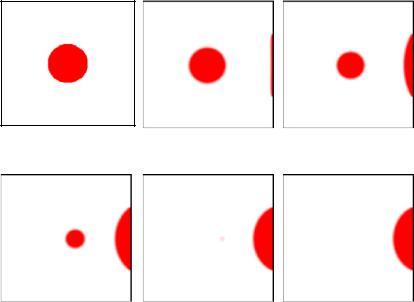
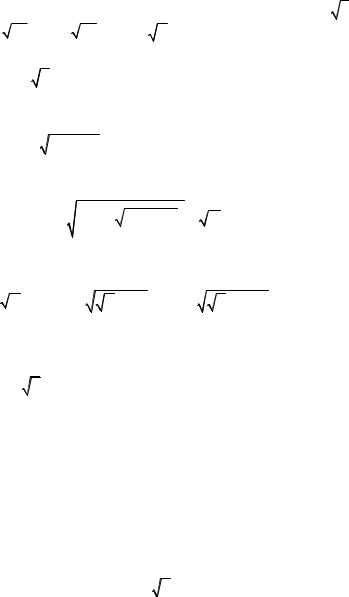Для значений при μ ~ 1, u0 = 10 m/s, σ0 = 1,91 N/m, ρ1 = 7800 kg/m3 и ν = 3·10–6 m2/s, km ≈ 10–7 m–1, C0 ≈ 10 выпол-

нение условия (8) возможно при значении скорости больше

300 m/s.

Таким образом, механизм образования наноструктур на поверхности рельсовой стали в процессе изнашивания заключается в возникновении неустойчивости Кельвина–Гельмгольца границы раздела слоев в зоне контакта колеса и рельса.

Исследование выполнено за счет гранта Российского научного фонда (проект № 15-12-00010).

Список литературы

1.Nanostructure formation on the surface of railway tracks / W. Lojkowski, M. Djahanbakhsh, G. BuÈrkle, S. Gierlotka, W. Zielinski, H.-J. Fecht // Mater. Sci. and Eng. A. – 2001. – Vol. 303.− P. 197–208.

2.The mechanism of formation of nanostructure and dissolution of cementite in a pearlitic steel during high pressure torsion / Yu. Ivanisenko, W. Lojkowski, R.Z. Valiev, H.-J. Fecht // Acta Mater. –2003. – Vol. 51. – P. 5555–5570.

3.Tarasov S.Y., Rubtsov V.E. Shear instability in the subsurface layer of a material in friction // Physics of Solid State. – 2011. – Vol. 53. – P. 358–362.

4.Tarasov S.Y., Rubtsov V.E., Kolubaev A.V. Subsurface shear instability and nanostructuring of metals in sliding // Wear. – 2010. – Vol. 268. – P. 59–66.

5.Granovskii A.Y., Sarychev V.D., Gromov V.E. Model of formation of inner nanolayers in shear flows of material // Tech. Phys. – 2013. – Vol. 58. – P. 1544–1547.

6.Nanosized structure formation in metals under the action of pulsed electric-explosion-induced plasma jets / V.D. Sarychev, E.S. Vashchuk, E.A. Budovskikh, V.E. Gromov // Tech. Phys. Lett. – 2010. – Vol. 36. – P. 656–659.

398

НЕЧЕТКИЙ КЛЕТОЧНЫЙ АВТОМАТ ДЛЯ МОДЕЛИРОВАНИЯ ЭФФЕКТА ТЕМПЕРАТУРНОЙ ПАМЯТИ

И.П. Селетков1, М.А. Марценюк2

(Пермский государственный национальный исследовательский университет,

Пермь, Россия, 1iseletkov@gmail.com, 2mrcn@psu.ru)

Рассматривается модель клеточного автомата с памятью, построенная с использованием нечеткой логики. Показано, что использование методов нечеткой логики в моделях клеточных автоматов позволяет повысить гибкость алгоритмов, упростить формализацию знаний эксперта. В качестве конкретного примера обсуждается задача расчета динамического изменения поля температуры с заданными граничными условиями. Показано, как предложенная модель позволяют учитывать эффект температурной памяти.

Ключевые слова: нечеткая логика, клеточный автомат, температурная память.

Классические модели клеточных автоматов [1, 2] подразумевают под собой функционал клеточных комбинационных схем. Фактически хранится и используется только текущее значение исследуемой величины в каждой клетке. При этом история изменения значений в клетках никак не анализируется.

Вработе [3] предложена модель «четкого» клеточного автомата с памятью, в которой для каждой ячейки, кроме значения основной исследуемой величины, хранится «состояние», отражающее историю изменения исследуемой величины.

Вработе авторов [4] предложена также модель нечеткого клеточного автомата с памятью (НКАП). По аналогии с «четкими» клеточными автоматами НКАП состоит из массива клеток, содержащих информацию о текущем значении исследуемой величины и истории ее изменения, а также вычислительное устройство (логический автомат), определяющее переходы клеток между состояниями. Вычислительное устройство представляет собой нечеткий автомат.

399

Рассмотрим построение такого автомата на конкретном примере. Недавние исследования [5–6] показывают, что уравнение теплопроводности в общем случае содержит слагаемое, зависящее от температуры среды в предшествующие моменты времени. Иными словами, среда обладает температурной памятью: q (x,t ) = −χ T (x,t ) − ξ T (x,t ) , где T (x,t ) – так называемое

t

температурное смещение T (x,t ) = T (x,0) + T (x,s)ds .

0

Введем параметры задачи и области их определения (универсальные множества): T – температура образца, T [0,300] °C,

τti , j – температура i, j -го элемента образца (ячейки) в момент

времени t.

Предположим, что в данный момент уже рассчитано значение температуры в ячейке i, j без учета эффекта температур-

ной памяти (часть с коэффициентом χ). Это можно сделать с помощью широко известных методов конечных разностей [7] и конечных элементов [8] или, например, с помощью нечеткой клеточной комбинационной схемы, описанной в [4].

Определим вклад температурной памяти (с коэффициентом ξ). Для этого найдем среднее за определенное количество шагов по времени значение температуры в ячейке:

400