
Математическое моделирование и основы научных исследований в сварке
..pdfМинистерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Пермский национальный исследовательский политехнический университет»
И.Ю. Летягин
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
ИОСНОВЫ НАУЧНЫХ ИССЛЕДОВАНИЙ
ВСВАРКЕ
Ч. 1. Статистическая обработка и планирование эксперимента
Утверждено Редакционно-издательским советом университета
в качестве учебного пособия
Издательство Пермского национального исследовательского
политехнического университета
2014
Стр. 1 |
ЭБ ПНИПУ (elib.pstu.ru) |
УДК 621.791.75 Л52
Рецензенты:
д-р техн. наук, проф. Е.А. Кривоносова (Пермский национальный исследовательский политехнический университет);
канд. воен. наук В.В. Дзябко (Пермский военный институт внутренних войск МВД России)
Летягин, И.Ю.
Л52 Математическое моделирование и основы научных исследований в сварке : учеб. пособие. Ч. 1. Статистическая обработка и планирование эксперимента / И.Ю. Летягин. – Пермь : Изд-во Перм. нац. исслед. политехн. ун-та, 2014. – 140 с.
ISBN 978-5-398-01231-6
Приведены основные сведения о методах статистической обработки экспериментальных данных. Рассмотрена методика планирования эксперимента. Приведены примеры из области сварочного производства. Все расчеты, приведенные в учебном пособии, выполнены в математическом пакете Mathcad. Приведены подробные алгоритмы расчетов и построения графиков с использованием пакета Mathcad. Рекомендовано при изучении дисциплин «Математические методы в инженерии», «Основы научных исследований, организация и планирование эксперимента» для студентов старших курсов и аспирантов сварочных специальностей и может быть полезно инженерам и научным работникам. Для усвоения представленного материала достаточно знаний в области теории вероятности, математической статистики и матричной алгебры, предусмотренных вузовским курсом математики.
УДК 621.791.75
ISBN 978-5-398-01231-6 |
© ПНИПУ, 2014 |
Стр. 2 |
ЭБ ПНИПУ (elib.pstu.ru) |
ОГЛАВЛЕНИЕ |
|
ВВЕДЕНИЕ............................................................................................................... |
5 |
1. СТАТИСТИЧЕСКАЯ ОБРАБОТКА................................................................... |
6 |
1.1. Статистическая обработка экспериментальных данных............................... |
6 |
1.1.1. Основные понятия и определения теории вероятностей |
|
и математической статистики........................................................................... |
6 |
1.1.2. Плотность и интегральная функция распределения |
|
случайных величин............................................................................................ |
8 |
1.1.3. Основные параметры теоретического и эмпирического |
|
распределения.................................................................................................... |
9 |
1.1.4. Техника вычисления параметров эмпирического распределения...... |
14 |
1.1.5. Нормальное распределение................................................................... |
15 |
1.1.6. Нормированная функция Лапласа........................................................ |
16 |
1.1.7. Некоторые выборочные распределения, применяемые |
|
при статистических исследованиях................................................................ |
18 |
1.1.8. Статистические функции в пакете Mathcad......................................... |
21 |
1.1.9. Статистическая обработка осциллограмм сварочного тока.............. |
25 |
2. ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА ПРИ ИССЛЕДОВАНИИ |
|
ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА ................................................................. |
32 |
2.1. Регрессионный анализ при обработке результатов |
|
пассивного эксперимента....................................................................................... |
32 |
2.2. Основные понятия и определения при планировании эксперимента ........ |
34 |
2.3. Полный факторный эксперимент................................................................... |
39 |
2.4. Матрицы планирования при большом числе факторов............................... |
41 |
2.5. Дробный факторный эксперимент................................................................. |
42 |
2.6. Свойства матриц полного и дробного факторных экспериментов............. |
44 |
2.7. Пример применения метода Бокса–Уилсона................................................. |
45 |
2.8. Обработка результатов эксперимента при отсутствии |
|
дублирования опытов............................................................................................. |
47 |
2.9. Крутое восхождение по поверхности отклика.............................................. |
50 |
2.10. Установление вида зависимости между двумя |
|
переменными величинами..................................................................................... |
53 |
2.11. Обобщенный параметр оптимизации........................................................... |
55 |
2.12. Принятие решений в экстремальном эксперименте.................................. |
58 |
2.13. Функции для проведения регрессии в пакете Mathcad.............................. |
60 |
|
3 |
Стр. 3 |
ЭБ ПНИПУ (elib.pstu.ru) |
3. МАТРИЧНЫЙ ПОДХОД К РЕГРЕССИОННОМУ АНАЛИЗУ...................... |
62 |
3.1. Метод наименьших квадратов для одного фактора..................................... |
62 |
3.2. Некоторые операции над матрицами............................................................. |
65 |
3.3. Матричный метод и регрессионный анализ.................................................. |
71 |
4. ФАКТОРНЫЙ ЭКСПЕРИМЕНТ ВТОРОГО ПОРЯДКА................................ |
79 |
4.1. Общие положения............................................................................................ |
79 |
4.2. Ортогональное планирование второго порядка............................................ |
80 |
4.3. Ротатабельное планирование второго порядка............................................. |
82 |
4.4. Принятие решений по планам второго порядка............................................ |
88 |
4.5. Техника канонического преобразования....................................................... |
91 |
5. ПРИМЕНЕНИЕ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТОВ |
|
ПРИ ИССЛЕДОВАНИИ СВАРОЧНЫХ ПРОЦЕССОВ ..................................... |
93 |
5.1. Исследование технологии сварки в узкую разделку ................................... |
93 |
5.2. Оптимизация процесса вибродуговой наплавки в углекислом газе.......... |
101 |
5.3. Оптимизация состава электродного покрытия............................................ |
116 |
5.3.1. Оптимизация состава по стабильности горения |
|
сварочной дуги............................................................................................... |
121 |
5.3.2. Оптимизация состава покрытия по критической |
|
температуре хрупкости металла шва........................................................... |
128 |
5.3.3. Оптимизация состава покрытия по обобщенной |
|
функции желательности................................................................................ |
132 |
СПИСОК ЛИТЕРАТУРЫ.................................................................................... |
139 |
4
Стр. 4 |
ЭБ ПНИПУ (elib.pstu.ru) |
ВВЕДЕНИЕ
Статистическая обработка экспериментальных данных и планирование эксперимента как метод оптимизации и исследований технологических процессов являются мощным средством достижения требуемых результатов в руках исследователя.
При проведении экспериментальных работ всегда наблюдается разброс полученных результатов. В этом смысле говорят, что результаты измерений – это случайная величина. Появление таких случайных результатов связано либо со случайной природой самого исследуемого явления, либо с различными случайными воздействиями, которые невозможно проконтролировать. Математическая статистика изучает методы обработки результатов наблюдений (измерений) массовых случайных явлений, обладающих статистической устойчивостью, закономерностью, с целью выявления этой закономерности.
Разработке нового технологического процесса сварки и его реализации, созданию новых сварочных материалов, как правило, предшествует изучение имеющихся теоретических и экспериментальных данных, проведение проверочного эксперимента, разработка проекта (новой технологии, новых сварочных материалов и т.д.) и оптимизация условий ведения процесса. До сих пор значительная часть исследований традиционно проводится по схеме изучения влияния отдельных факторов.
Необходимо отметить, что современные сварочные технологические процессы сложны, многомерны и подвержены влиянию различных помех. Стабилизация условий проведения опытов в них часто является невыполнимой задачей, поэтому традиционная схема исследований в таких условиях становится малоэффективной. Кроме того, совокупное действие отдельных факторов (переменных) не всегда равно простой их сумме из-за явления взаимодействия между факторами.
Как правило, технологические исследования связаны со значительными энергетическими и материальными затратами, трудоемки, поэтому одной из важнейших задач исследователя является достижение искомого результата оптимальным образом. Планирование эксперимента предлагает исследователю огромную разновидность планов или программ их построения, методов обработки экспериментальных данных для различных встречающихся практических задач.
5
Стр. 5 |
ЭБ ПНИПУ (elib.pstu.ru) |
1.СТАТИСТИЧЕСКАЯ ОБРАБОТКА
1.1.СТАТИСТИЧЕСКАЯ ОБРАБОТКА
ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
Исследуемые параметры объекта (процесса, явления) в ряде случаев представляют собой не зависящие друг от друга случайные величины. Иногда эти зависимости связаны между собой какой-либо функциональной или коррелятивной зависимостью. Нахождение вида связи между параметрами объекта является важной областью экспериментальных работ. Результат эксперимента независимо от его назначения получается в виде набора чисел. Для того чтобы воспользоваться результатами проведенного опыта и делать на основании его какие-либо обобщения и выводы, требуется предварительно произвести статистическую обработку всех материалов эксперимента. Статистическая обработка эмпирических данных сводится (в общем виде) к следующему:
−вычислению определенных характеристик объекта;
−определению теоретических характеристик объекта по их экспериментальным значениям;
−сравнению по определенным критериям экспериментальных значений характеристик с заданными теоретическими;
−сравнению эмпирических и теоретических функций по определенным критериям согласия;
−установлению вида зависимости между случайными величинами.
1.1.1. Основные понятия и определения теории вероятностей и математической статистики
Испытанием или опытом называется реализация некоторых правил, условий. Например, испытанием будет рентгеноконтроль сварных швов, определение величины и количества дефектов и т.д. В теории вероятностей обычно рассматриваются массовые испытания, т.е. испытания, происходящие неоднократно при неизменных основных условиях. Явление, получающееся в результате испытания, называется событием.
6
Стр. 6 |
ЭБ ПНИПУ (elib.pstu.ru) |

Виды событий:
–событие называется достоверным, если в результате данного испытания оно обязательно произойдет;
–событие называется невозможным, если в результате данного испытания оно произойти не может;
–событие называется случайным (или возможным), если в результате данного испытания оно может произойти, но может и не произойти;
–два события называются несовместными, если при испытании появление одного из них исключает возможность появления другого;
–два события называются совместными, если при испытании появление одного из них не исключает возможность появления другого;
–события называются единственно возможными, когда при испытании произойдет хотя бы одно из этих событий;
–если при испытании могут появиться несколько возможных событий, и при этом нет основания предполагать, что появление одних вероятнее появления других, тотакие события называются равновозможными.
Вероятность события – это отношение числа случаев, благоприятствующих наступлению данного события, ко всему числу несовместных, единственно возможных и равновозможных событий:
P( A) = m ,
N
где P (A) – вероятность события А; m – число случаев, соответствующих наступлению события А; N – число несовместных, единственно возможных и равновозможных событий.
Если m = N, то P (A) = 1 − событие А достоверно. Если m = 0, то Р (А) = 0 − событие А невозможно.
Случайной величиной называют величину, которая в результате опыта может принимать различные значения. Например, величина глубины проплавления при сварке есть случайная величина, которая может принимать различные значения в определенном интервале.
Случайные величины обычно обозначают большими буквами, например Х. Значения случайной величины, которые она принимает в результате опыта, обозначают малыми буквами x1, x2, …, xn. При массовых испытаниях каждое из возможных значений случайной величины x1, x2, …, xn может встретиться m1, m2, …, mn раз. Эти числаназываютчастотами. Если всего было проведено N испытаний, т.е.
7
Стр. 7 |
ЭБ ПНИПУ (elib.pstu.ru) |
n
∑mi = N ,
i=1
то отношение mi / N называют частостью или относительной частотой. Совокупность, содержащая все исследуемые объекты, называется
генеральной совокупностью. Выбранные из генеральной совокупности N объектов образуют выборку объемом N.
Дискретными случайными величинами называются такие, которые могут принимать лишь определенные значения, например 0,1; 0,2;
0,3 и т.д.
Непрерывными случайными величинами называются такие, которые в некотором интервале могут принимать любые значения. Например, число бракованных изделий в различных выборках из генеральной совокупности есть дискретная случайная величина, а размер сварочных дефектов − непрерывная случайная величина. Всякую непрерывную случайную величину можно задать в виде дискретной, если все возможные ее значения разбить на интервалы и задать вероятность появления этих интервалов.
1.1.2. Плотность и интегральная функция распределения случайных величин
Если Х случайная величина, а х – некоторое ее значение, то вероятность того, что Х < х,
F (x) = P (X < x),
где F (x) − некоторая функция, называемая интегральной функцией распределения (рис. 1, где F (x) − ординаты кривой в некоторой точке х). При любом х 0 ≤ F (x) ≤ 1.
Плотность вероятности ϕ (х) есть предел отношения вероятности того, что случайная величина Х примет значение, лежащее между
х и х + ∆ х, к величине интервала ∆ х при ∆ х → |
0: |
|
||
φ( X ) = lim |
P(x ≤ |
X≤ |
x+ ∆ x) |
. |
|
∆ x |
|
||
∆ x→ 0 |
|
|
||
Графически плотность вероятности случайной величины представлена на рис. 2.
8
Стр. 8 |
ЭБ ПНИПУ (elib.pstu.ru) |
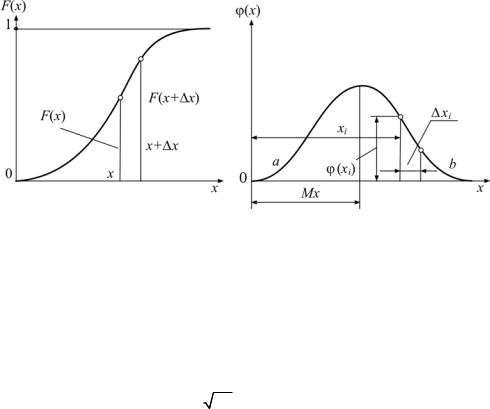
Рис. 1. Интегральная функция |
Рис. 2. Плотность вероятности |
распределения |
случайной величины |
Будем считать, что случайная величина задана теоретическим законом, если заданы ее интегральный закон или ее плотность вероятности. Законов распределения плотности в статистической обработке множество. Наибольшее применение находит нормальныйзакон(закон Гаусса):
|
1 |
|
|
( x − a)2 |
||
φ(x) = |
|
exp |
− |
2σ2 |
. |
|
σ 2π |
||||||
|
|
|
|
|||
|
|
|
|
|
|
|
Случайная величина задана эмпирическим законом распределения, если для каждого значения случайной величины известна частота встречаемости, полученная из N опытов (табл. 1).
|
|
|
|
|
Таблица 1 |
|
|
|
|
|
|
|
|
Значения X |
x1 |
x2 |
x3 |
… |
|
xn |
Частоты |
m1 |
m2 |
m3 |
… |
|
mn |
Частости |
m1/N |
m2/N |
m3/N |
… |
|
mn/N |
При N →∞ |
mi/N → P (X). В пределе частости стремятся к вероят- |
|||||
ностям соответствующих значений случайной величины.
1.1.3.Основные параметры теоретического и эмпирического распределения
Наиболее часто употребляемыми характеристиками случайной величины служат моменты и квантили.
9
Стр. 9 |
ЭБ ПНИПУ (elib.pstu.ru) |
Первым центральным моментом случайной величины Х является математическое ожидание МХ (или среднее значение).
Для дискретной случайной величины
n
MX = ∑ xi P(xi ).
i =1
Для непрерывной случайной величины, заданной своей плотностью вероятности ϕ (x),
b
MX= ∫ x ϕ (x)dx .
a
Эмпирическое распределение характеризуется средним значением
|
|
N |
|
|
|
∑ xi |
|
xcp |
= |
i=1 |
. |
|
|||
|
|
N |
|
При достаточно большом N выборочное значение xср стремится по величине к математическому ожиданию, т.е. xср = МХ.
Свойства математического ожидания:
−математическое ожидание постоянной равно этой постоянной;
−математическое ожидание суммы случайных величин равно сумме их математических ожиданий, т.е.
M (X + Y) = MX + MY;
− математическое ожидание произведения случайной величины на константу равно произведению этой константы на математическое ожидание случайной величины, т.е.
MaX = aMX.
Кроме среднего значения случайной величины, которое характеризует центр распределения вероятностей, большое значение имеет и разброс случайной величины относительно этого центра. Для количественного описания этого разброса в теории вероятностей используют второй центральный момент случайной величины, который в отечественной технической литературе называют дисперсией и обозначают че-
10
Стр. 10 |
ЭБ ПНИПУ (elib.pstu.ru) |
