Математическое моделирование в естественных науках

го университета. Аэрокосмическая техника. – 2015. – № 41. –

С. 103–119.

3. Лебединский Е.В., Калмыков Г.П., Мосолов С.В. Рабочие процессы в жидкостном ракетном двигателе и их моделирование / под ред. А.С. Коротеева. – М.: Машиностроение, 2008. – 512 с.

О ЧИСЛЕННОМ ИССЛЕДОВАНИИ РАЗМЕРОВ И ЗАКОНА ДВИЖЕНИЯ ВИХРЕВОГО КОЛЬЦА

И.В. Храмцов, П.В. Писарев, В.В. Пальчиковский

(Пермский национальный исследовательский политехнический университет,

Пермь, Россия, igorhrs92@mail.ru)

Рассматривается задача численного моделирования интенсивных вихревых течений на примере элементарного объекта гидродинамики – вихревого кольца. Проведены расчеты в ANSYS CFX формирования вихревого кольца поршневым генератором. Проведена оценка геометрических размеров и движения вихря. Результаты численного моделирования соответствуют результатам, полученным в эксперименте и автомодельной теории движении вихревого кольца.

Ключевые слова: вихревое кольцо, турбулентные вихри, численное моделирование, ANSYS CFX, аэроакустика.

Вихревое кольцо является элементарным объектом аэроакустики. Будучи созданным, данный вихрь развивается только под действием собственной динамики, не испытывая влияния твердых границ. Это позволяет исследовать с его помощью многие вопросы гидродинамики в чистом виде. Вихревое кольцо обладает богатым набором характерных акустических проявлений: излучение на дискретных частотах, резонансное поглощение звука и т.д. При этом оно доступно для экспериментального изучения.

Геометрические размеры локализованных вихрей являются важнейшим параметром для построения теорий генерации шума данными вихрями. В частности, в работах [1, 2] приводит-

461

ся теоретическая модель излучения шума турбулентным вихревым кольцом в зависимости от параметров, измеряемых в эксперименте: R, μ = a/R, V, α, где V – поступательная скорость вихревого кольца, R – радиус вихревого кольца, a – радиус ядра вихревого кольца, α – коэффициент скорости роста вихревого кольца. Данная работа посвящена оценке данных параметров при численном моделировании.

Для численного моделирования используется геометрическая модель поршневого генератора вихревых колец используемого для аэроакустических исследований в Центральном аэрогидродинамическом институте (Москва). Численные эксперименты проводились в многопроцессорном инженерном вычислительном комплексе ANSYS CFX в осесимметричной нестационарной постановке с учетом вязкости и сжимаемости течения. Расчеты выполнены на кластере Центра высокопроизводительных вычислительных систем ПНИПУ. Использовалось до 64 ядер, что позволилосократить время расчетадонескольких дней.

По результатам расчетов строились зависимости радиуса вихревого кольца и его перемещения от времени. Оценка положения вихря определялась по положению центра вихревого кольца, в качестве которого была принята точка, в которой плотность, давление и температура являются минимальными. Полученные зависимости сравнивались с автомодельной теорией движения вихревого кольца по методике, представленной в [3, 4]. Полученные в результате характеристики хорошо согласуются с данной теорией и результатами экспериментов:

U0 = 37 м/с, R0 = 0,031 м, α = 0,003.

Для оценки радиуса ядра вихревого кольца использовались численные шлирен-фотографии [5]. При этом методе отображается распределение нелинейных функций модуля градиента плотности. Данный метод эквивалентен теневым методам визуализации течений, что позволяет сравнить результаты численного расчета и экспериментов по визуализации вихревых течений. Оценка размеров производилась по точкам, в которых

462

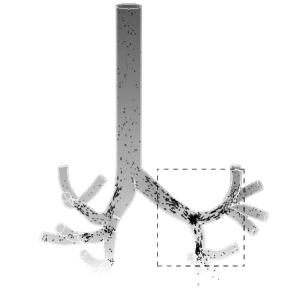
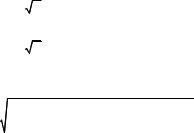наблюдаются наибольшие значения модуля градиента плотности. В результате было получено наблюдение, что ядро вихревого кольца имеет форму эллипса, вытянутого в осевом направлении, с безразмерным размером μ ≈ 0,14–0,2, что хорошо согласуется с результатами визуализации [6].

Работа выполнена при поддержке гранта Правительства РФ по п. 220.

Список литературы

1.Зайцев М.Ю., Копьев В.Ф. О смещении пика в спектре излучения вихревого кольца // Ученые записки ЦАГИ. – 1998. –

Т. XXIX, № 3–4.

2.Зайцев М.Ю., Копьев В.Ф. О механизме излучения звука турбулентным вихревым кольцом // Акустический журнал. – 1993. – Т. 39, вып. 6. – С. 1068–1075.

3.Моделирование формирования и динамики вихревого кольца / И.В. Храмцов, П.В. Писарев, В.В. Пальчиковский, Р.В. Бульбович // Вестник Пермского национального исследовательского политехнического университета. Аэрокосмическая техника. – 2014. – № 39. – С. 127–144.

4.Numerical analysis of gasdynamic characteristics of vortex ring / I.V. Khramtsov, P.V. Pisarev, V.V. Palchikovskiy, R.V. Bulbovich, V.V. Pavlogradskiy // Applied Mechanics and Materials. – 2015. – Vol. 770. – P. 483–490.

5.Горячев В.Д., Балашов М.Е., Смирнов Е.М. Визуализация нестационарных течений в вычислительной гидродинамике / Научный сервис в сети интернет: суперкомпьютерные центры

изадачи: тр. междунар. суперкомпьютер. конф. – М.: Изд-во МГУ, 2010. – C. 50–55.

6.A technique for visualization of the turbulent vortex ring / V.F. Kopiev, M.Yu. Zaitsev, L.P. Guriashkin, V.A. Yakovlev // Atlas of Visualization. – 1996. – Vol. 2. – P. 139–149.

463

ИССЛЕДОВАНИЕ ТЕЧЕНИЯ ВОЗДУХА В ВОЗДУХОНОСНЫХ ПУТЯХ ЧЕЛОВЕКА

М.Ю. Цинкер1, П.В. Трусов2

(1Федеральный научный центр медико-профилактических технологий управления рисками здоровью населения, Пермь, Россия, cinker@fcrisk.ru, 2Пермский национальный исследовательский политехнический университет,

Пермь, Россия, tpv@matmod.pstu.ac.ru)

Статья посвящена трехмерному моделированию процесса течения воздуха в крупных дыхательных путях человека. На основе данных медицинских атласов была воссоздана трехмерная геометрия первых четырех генераций нижних дыхательных путей, начиная с трахеи. С использованием программного продукта ANSYS Fluent выполнен расчет течения воздуха при вдохе и выдохе

Ключевые слова: математическое моделирование, течение воздуха, крупные воздухоносные пути человека.

Работа посвящена математическому моделированию дыхательной системы человека [1]. Полная математическая модель дыхательной системы является многоплановой и состоит из трех связанных подмоделей, описывающих процесс дыхания как совокупность синхронизированных процессов газовой динамики, упругих деформаций, диффузии, каждый из которых имеет свои особенности. В данной статье рассмотрен фрагмент работы, посвященной одной из подзадач – трехмерному моделированию процесса течения в крупных воздухоносных путях человека, так как данный участок дыхательной системы имеет сложную ассиметричную геометрию и свои особенности потока воздуха, которые необходимо учитыватьпри моделированиидыхательной системы.

Дыхательная система представлена первыми четырьмя генерациями нижних воздухоносных путей, начиная с трахеи. Движение воздуха в воздухоносных путях осуществляется благодаря разности давлений между легкими и атмосферой (из области высокого в область низкого давления).

464

Трехмерная геометрия воздухоносных путей была воссоздана на основе данных медицинских атласов [2, 3]. С использованием программного продукта ANSYS Fluent выполнен расчет течения воздуха в крупных воздухоносных путях. Расчет проводился для двух сценариев (вдох и выдох).

В начальный момент времени давление однородно и скорость течения воздуха равна нулю. На входе в трахею задается давление, равное атмосферному. При вдохе давление на выходе из бронхов задается на 2 мм рт. ст. меньше атмосферного. При выдохе давление на выходе из бронхов задается на 4 мм рт. ст. больше атмосферного. На стенках воздухоносных путей задаются условия непроницаемости.

Получены параметры течения воздуха на вдохе и выдохе. На рис. 1 представлены поля вектора скорости перемещений на выдохе.

Рис. 1. Поле вектора скорости на выдохе: фронтальная плоскость, вид спереди

465

По мере уменьшения размера воздухоносных путей уменьшаются скорости течения. Это обусловлено тем, что суммарная площадь сечений на входе в легкие больше площади поперечного сечения трахеи. В местах сужения и ветвления наблюдается увеличение скоростей течения воздуха и возникновение завихренности течения (рис. 2).

Рис. 2. Поле вектора скорости на выдохе: фронтальная плоскость, вид спереди (укрупненный фрагмент, отмеченный на рис. 1)

Таким образом, в рамках математической модели дыхательной системы человека получены параметры течения воздуха в крупных воздухоносных путях на вдохе и выдохе. Данные, почерпнутые из решения задачи газодинамики в воздухоносных путях человека, являются входными для решения задачи течения воздуха в легких. Применение разрабатываемой полной модели дыхательной системы позволит оценивать поступление веществ из окружающей среды в кровеносную систему, имитировать негативное действие факторов среды обитания на организм человека и строить прогнозы функционального состояния дыхательной системы человека.

466

Список литературы

1.Цинкер М.Ю. Дыхание человека как биомеханический процесс. Математическое моделирование в естественных науках: материалы XXIII Всерос. школы-конф. молодых ученых

истудентов. – Пермь: Изд-во Пермского национального исследовательского политехнического университета, 2014. – Т. 1. –

С. 290–292.

2.Синельников Р.Д., Синельников Я.Р. Атлас анатомии человека: учеб. пособие. – 2-е изд., стер. – М.: Медицина, 1996. –

Т. 2. – 264 с.

3.Вейбель Э.Р. Морфометрия легких человека. – М.: Ме-

дицина, 1970. – 176 с.

ЭКСПЕРИМЕНТАЛЬНЫЕ И ТЕОРЕТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ТЕКСТУРЫ МАТЕРИАЛА

В.А. Частоедов1, Н.С. Кондратьев2

(Пермский национальный исследовательский политехнический университет,

Пермь, Россия, 1v.a.chastoedov@mail.ru, 2kondratevns@gmail.com)

Рассматриваются проблемы анализа свойств текстурированных материалов и процедура сравнения полюсных фигур, полученных теоретически в физических моделях неупругого деформирования и экспериментально. В качестве математического аппарата сравнительного анализа используется вейвлет-преобразование. Предложен и численно реализован алгоритмсравнениятеоретических иэкспериментальныхданных.

Ключевые слова: физические теории пластичности, неупругое деформирование, вейвлет-анализ.

Практически все сферы деятельности человека нуждаются в создании новых или улучшении качества существующих материалов. Многочисленные эксперименты и теоретические исследования показывают, что свойства поликристаллических материалов и их поведение на макроуровне в процессе неупругого

467

деформирования существенным образом определяются состоянием эволюционирующих мезо- и микроструктур. Под эволюцией мезоструктуры здесь понимаются процессы разворотов кристаллических решеток зерен или их фрагментов, а также их фрагментация и дробление. Под эволюцией микроструктуры в первую очередь понимаются изменения в дефектной структуре материала на микроуровне (уровне дислокационных субструктур, границ зерен и т.д.) [1]. Макронагружения являются источником эволюции выше отмеченной внутренней структуры, которая в свою очередь приводит к изменению отклика материала на макроуровне. Таким образом, можно управлять свойствами материала, изменяя его мезо- и микроструктуры, определяющие рабочие характеристики готовых деталей и конструкций. В настоящее время существуют модели (например, статистические физические теории пластичности), способные описать внутреннюю структуру материала, в том числе и распределение ориентаций кристаллитов (зерен) внутри поликристалла [1].

При описании неупругого деформирования в моделях физических теорий пластичности важную роль играет ориентация отдельных кристаллитов в поликристалле. Под внешним воздействием зерна начинают поворачиваться и образовывать кристаллографические текстуры, т.е. преимущественные ориентации. В процессе образования текстуры, как правило, поликристаллический материал приобретает анизотропию свойств [2]. Таким образом, актуальность построения модели неупругого деформирования, описывающей в том числе текстурообразование, подтверждается достаточно острой необходимостью ее применения для исследования технологических процессов с целью улучшения свойств материала и предотвращения негативных эффектов [3].

Вопросы идентификации параметров модели в целом и модели ротации в частности являются ключевой проблемой. Для решения последней задачи необходимо предложить способ

468

определения «близости» модельных и экспериментальных данных ориентаций зерен макрообъема. Как правило, такие данные представляют собой полюсные фигуры, и для их сравнительного анализа перспективным представляется подход, основанный на вейвлетах [4, 5].

Работа посвящена проблеме сравнения полюсных фигур, полученных посредством физически моделей неупругого деформирования, с экспериментальными данными. Сложность сопоставления заключается в оцифровке исходного сигнала, т.е. в переходе от изображения экспериментальной полюсной фигуры к массивам данных, и представление их в едином формате

стеоретическими результатами. Поскольку на данном этапе работы вопросы оцифровки были мало изучены, дальнейшие исследования проводились с использованием самостоятельно задаваемыми полюсными фигурами.

Важнейшей частью работы является сравнение массивов данных, полученных теоретически и экспериментально. С этой целью применяется математический аппарат вейвлетов, хорошо зарекомендовавший себя в задачах, связанных

санализом пространственных полей со сложной многомасштабной структурой, либо временных сигналов с меняющимся со временем спектральным составом. Вейвлет-преобра- зование основывается на разложении сигнала (массива данных) по базису солитоноподобной функции по средствам масштабных изменений и переносов [5]. Такое преобразование способно анализировать локализованные функции и функции, имеющие точки разрыва, а также использовать различные анализирующие (базисные) функции, удовлетворяющие некоторым условиям. В результате вейвлет-преобразования имеются частотно-временные характеристики сигнала, которые и сравниваются по степени «похожести».

Непрерывное вейвлет-преобразование и корреляционная функция двух сигналов имеют вид:

469

анализирующий вейвлет (звездочка обозначает комплексное сопряжение), который получается вращением одномерного вейвлета вокруг выделенной оси; t – радиус-вектор, зависящий от двух пространственных координат; а ‒ масштаб; b ‒ вектор сдвига двух пространственных координат.

В серии численных расчетов входными параметрами являются полюсные фигуры. Для создания полюсной фигуры ориентация кристаллитов задавалась углами Эйлера по равномерному закону распределения направлений по сфере, и получившиеся направления преобразовывались в плоское изображения по методу стереографической проекции. На полученные полюсные фигуры накладывалась равноплощадочная сетка, и подсчитывалось количество точек в каждой ячейке. В результате получился массив данных, где номер ячейки соответствует координатам центра площадки на сетке, а значение – количеству точек. Полученные таким образом массивы интенсивности подвергались вейвлет-преобразованию. Последним шагом является вычисление корреляционной функции, зная функции вейвлет коэффициентов.

В ходе работы был разработан алгоритм для задачи о сравнении двух прямых полюсных фигур. Получены соотно-

470