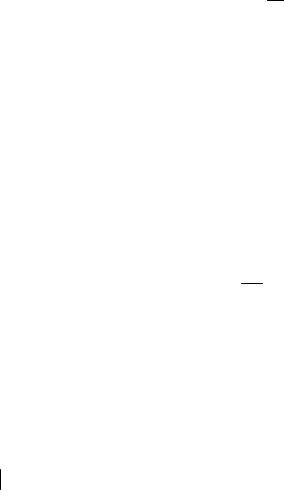A = {α = (a1,a2 , ..., aL ) : ai− ≤ ai ≤ ai+ , i = 1, L}.
Считается, что клинические данные можно получить в узлах сетки
|
|
|
|
|
T |
|
|
|
|
Π = ti |
: ti |
= i t, i = 0, N, t = |
|
. |
|
|
|
|
|
|
N |
В качестве цели управления выбран перевод системы из устойчивой хронической формы заболевания в состояние здорового организма:
v(t) → 0, |
v(0) = v . |
t→∞ |
0 |
Управляющая функция, характеризующая скорость введения донорских антител, выбирается из множества
U ={u(t) : u(t) = ui−1 [0, B], t [ti−1, ti ), i =1, N, u(T ) = uN −1}.
Для оценки параметров и построения управления использовалась модификация алгоритма, предложенного в работе [3]. Значения параметров задавались случайным образом:
αk Θ, k = |
|
, Θ = |
α: a |
= a− + |
1, K |
|
|
|
|
ij |
i |
|
|
|
|
|
|
|
jh , j = |
|
, h = |
ai+ − ai− |
, i = |
|
. |
|
0,M |
1, L |
|
|
|
i |
i |
i |
Mi |
|
|
|
|
|
|
|
|
|
|
Был выбран следующий критерий идентификации:
y j (ti ,α(k ) ) − yэкспj |
. (ti ) |
< εj , i = |
0, N |
, k = |
1, Ki |
, j = |
1,m |
, |
где y(t) = {y1(t), y2 (t)}T = {v(t),m(t)}T , Ki – количество наборов
параметров в момент ti. Таким образом, для идентификации параметров использовались значения переменных инфекционного
процесса. |
|
выбирались сред- |
В качестве оценки параметров при t = t |
i |
|
|
ние значения допустимых наборов: |
|
|

Ji
a(jk )
|
|
|
j(i) = |
k=1 |
, j = |
1, L |
, i = |
0, N |
, |
|
a |
|
|
Ji |
|
|
|
|
|
|
|
|
|
где Ji – количество допустимых наборов параметров в мо-
мент ti.
Для каждого допустимого набора параметров с помощью метода, предложенного в работе [4], вычислялось значение управления ui(k ) , i =1, N, k =1, Ki . Идея алгоритма заключается
в том, что динамику антигенов нужно вывести на желаемое состояние. В случае хронической формы заболевания в качестве желаемого состояния выступает выведение антигенов из организма при острой форме. Управляющая функция представляет собой среднее значение найденных величин:
Ji
ui(k )
|
|
|
|
= |
k=1 |
, i = |
1, N |
. |
|
u |
i |
|
|
Ji |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В таблице представлены результаты идентификации параметров при τ = 0 и m = 0,1.
Параметры базовой модели инфекционного заболевания
Пара- |
a− |
a+ |
h |
|
Точное |
Погреш- |
Оценка |
значе- |
метр |
i |
i |
i |
|
ние |
ность, % |
|
|
|
|
|
|
a1 |
0,875 |
1,125 |
0,05 |
1,013 |
1 |
3,70 |
a2 |
0,55 |
1,05 |
0,1 |
0,800 |
0,8 |
0,00 |
a3 |
955 |
1055 |
10 |
1023 |
1000 |
2,30 |
a4 |
0,145 |
0,195 |
0,01 |
0,175 |
0,17 |
2,94 |
a5 |
0,25 |
0,75 |
0,1 |
0,425 |
0,5 |
15,00 |
a6 |
7,5 |
12,5 |
1 |
11,500 |
12 |
15,00 |
a7 |
0,095 |
0,145 |
0,01 |
0,125 |
0,12 |
4,17 |
a8 |
5,5 |
10,5 |
1 |
7,500 |
8 |
6,25 |
На рисунке показан вид управляющей функции. Сплошными линиями показано управление, построенное в условиях с неполной информацией, а штриховыми – управление с заданными значениями параметров. Отклонение объема введения донорских антител лежит в пределах 7 %.
Рис. Динамика антигенов
Таким образом, рассмотренный метод позволяет строить программу лечения в процессе измерения клинических показателей.
Список литературы
1.Марчук Г.И. Математические модели в иммунологии. –
М.: Наука, 1980. – 264 с.
2.Болодурина И.П., Луговскова Ю.П. Оптимальное управление иммунологическими реакциями организма человека // Про-
блемы управления. – 2009. – № 5. – С. 44–52.
3.Русаков С.В., Чирков М.В. Идентификация параметров
иуправление в математических моделях иммунного ответа // Российский журнал биомеханики. – 2014. – Т. 18, № 2. – С. 259–269.
4.Русаков С.В., Чирков М.В. Математическая модель влияния иммунотерапии на динамику иммунного ответа // Пробле-
мы управления. – 2012. – № 6. – С. 45–50.
ОПИСАНИЕ ИЗМЕНЕНИЯ ЗЕРЕННОЙ СТРУКТУРЫ В ДВУХУРОВНЕВЫХ МОДЕЛЯХ НЕУПРУГОСТИ МЕТАЛЛОВ
Е.В. Чудаков, А.И. Швейкин
(Пермский национальный исследовательский политехнический университет,
Пермь, Россия, chudakov@yandex.ru)
Для технологических процессов механической обработки металлов давлением актуальной является задача описания происходящих изменений зеренной структуры. В работе рассматривается двухуровневая конститутивная модель поликристаллического металла, включающая описание процесса дробления кристаллитов. С использованием модели численно реализовано нахождение напряженно-деформированного состояния сописанием изменениязереннойструктурыГЦК-поликристалла(медь).
Ключевые слова: двухуровневые конститутивные модели, физические теории пластичности, дробление зерен.
Одним из основных подходов к получению материалов с повышенными эксплуатационными свойствами является применение методов механической обработки с достижением значительных пластических деформаций, которое сопровождается возрастанием плотности дефектных субструктур и измельчением зеренной структуры. В последние годы возрастает интерес к получению с использованием данного подхода объемных субмикрокристаллических и наноструктурных материалов. Создание математических моделей, позволяющих описывать эволюцию мезо- и микроструктуры поликристаллических материалов при больших деформациях, позволит определять оптимальные режимы таких технологических процессов и поэтому является актуальной задачей механики деформируемого твердого тела [1].
Цель работы – включение описания дробления кристаллитов в структуру двухуровневой статистической упруговязкопластической модели неупругого деформирования поликристаллических металлов [2]. В конститутивной модели в соот-
ветствие представительному объему макроуровня ставится выборка кристаллитов, аппроксимированных эллипсоидами, для которых проводится описание основных физических механизмов неупругого деформирования: внутризеренного дислокационного скольжения с учетом упрочнения и ротаций решеток. Для описания внутризеренного дислокационного скольжения используется вязкопластический закон, как критерий активности процесса скольжения дислокаций по системам скольжения используется закон Шмида – равенство касательных напряжений на системе скольжения критическим [3]. При описании поворотов решетки кристаллитов используется либо модель поворота Тейлора [4], либо модель, учитывающая несовместность скольжения дислокаций в соседних кристаллитах [2]. Для конкретизации соотношений макромасштабного уровня используется условие согласования определяющих соотношений различных уровней [2].
При описании процесса дробления были приняты гипотезы о моменте дробления кристаллита (построенный критерий дробления основывается на анализе накопленных сдвигов по системам скольжения краевых дислокаций с учетом текущей геометрии зерна) и гипотеза о геометрии разделения: кристаллит разделяется на две равные части с упаковкой получающихся кристаллитов наиболее плотным образом. В первом приближении для упрощения численной реализации вместо решения задачи оптимизации, что необходимо при принятии второй гипотезы, полагается, что при выполнении критерия дробления ориентация получающихся кристаллитов одинакова и получается поворотом главного вектора вдоль наибольшей полуоси тензора формы исходного зерна к направлению сдвигатой системы скольжения, для которой выполняется критерий дробления.
Разработан алгоритм реализации двухуровневой модели на основе использования численных методов явного интегриро-
вания систем обыкновенных дифференциальных уравнений, создана вычислительная программа, с помощью которой проведены тестовые расчеты для различных нагружений поликристаллической меди. Получены результаты, в том числе описание изменения зеренной структуры, которые находятся в согласовании с известными опытными данными.
Работа выполнена при поддержке гранта Президента РФ № МК-4485.2014.1 и Российского фонда фундаментальных исследований (грант № 15-08-06866-а).
Список литературы
1.Определяющие соотношения и их применение для описания эволюции микроструктуры / П.В. Трусов, В.Н. Ашихмин, П.С. Волегов, А.И. Швейкин // Физическая мезомеханика. – 2009. –
Т. 12, № 3. – С. 61–71.
2.Многоуровневые модели неупругого деформирования материалов и их применение для описания эволюции внутренней структуры / П.В. Трусов, А.И. Швейкин, Е.С. Нечаева, П.С. Волегов // Физическая мезомеханика. – 2012. – Т. 15,
№1. – С. 33–56.
3.Швейкин А.И., Шарифуллина Э.Р. Анализ конститутивных соотношений для описания внутризеренного дислокационного скольжения в рамках двухуровневой упруговязкопластической модели ГЦК-поликристаллов // Вестник Тамбов. унта. Сер.: Естественные и технические науки. – 2013. – Т. 18,
вып. 4, ч. 2. – С. 1665–1666.
4.Швейкин А.И., Ашихмин В.Н., Трусов П.В. О моделях
ротации решетки при деформировании металлов // Вестник Пермского государственного технического университета. Механи-
ка. – 2010. – № 1. – С. 111–127.

КОНВЕКЦИЯ ВЯЗКОПЛАСТИЧЕСКОЙ ЖИДКОСТИ В ПРЯМОУГОЛЬНОЙ ПОЛОСТИ ПРИ НАГРЕВЕ СБОКУ
А.А. Шаниязов1, Т.П. Любимова1, 2
(1Пермский государственный национальный исследовательский университет, Пермь, Россия,
2Институт механики сплошных сред УрО РАН,
Пермь, Россия, lubimova@psu.ru)
Исследуется свободная тепловая конвекция вязкопластической жидкости в вытянутой по вертикали прямоугольной области при нагреве сбоку. Для описания реологического поведения жидкости используется модель Хершеля–Балкли. Задача решается численно с помощью пакета прикладных программ Ansys Fluent. Получены данные об изменении интенсивности течения и полей температуры и функции тока при изменении чисел Грасгофа и Бингама.
Ключевые слова: свободная тепловая конвекция, вязкопластическая жидкость, прямоугольная полость, численное исследование.
Работа посвящена исследованию свободной тепловой конвекции вязкопластической жидкости в вытянутой по вертикали прямоугольной области при нагреве сбоку. Границы области считаются твердыми, на них задаются условия прилипания. На вертикальных границах задаются постоянные разные температуры, горизонтальные границы теплоизолированы. Задача решается в рамках приближения Буссинеска. Для описания реологического поведения жидкости используется модель Хершеля–Балкли [1]. Кривая течения для этой жидкости приведена на рис. 1.
Реологическое уравнение жидкости Хершеля–Балкли имеет вид:
|
|
|
|
|
γ < τ0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
γ > τ0 / μ0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ = μ0 |
γ для |
/ μ0 , |
|
τ = |
τ0 + μ |
γ − τ0 / μ0 |
для |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ = (1/2) |
|
|
|
|
1 2 |
|
γ = |
|
|
|
|
|
|
|
|
|
1 2 |
|
γij = ∂ui |
/ ∂xj + ∂u j / ∂xi . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ |
: |
τ |
|
, |
(1/2)γ:γ |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
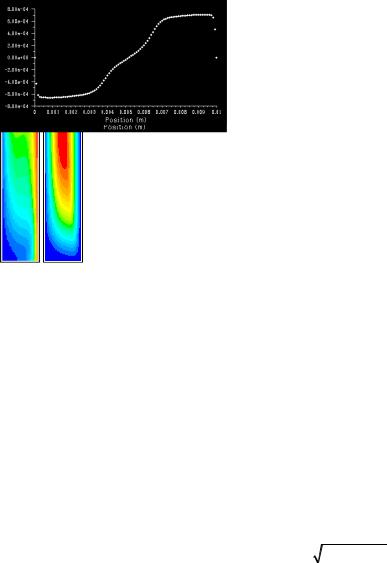
Рис. 1. Поля температуры и функции тока (слева), профили температуры (справа вверху) и вертикальной компоненты скорости (справа внизу) в горизонтальном сечении, y = H / 2 для жидкости
Хершеля–Балкли при Pr = 7, Ra = 106 , Bn = 10
Задача решалась с помощью коммерческого пакета Ansys Fluent 6.3.26, основанного на применении метода конечных объемов. Расчетная сетка строилась с помощью пакета Gambit 2.4. Основные расчеты проводились на равномерной сетке с квадратными ячейками, размер ячейки h = 0,0002. Расчеты проводились для отношения высоты полости к ширине, равного 8. Значения числа Прандтля и отношения μ0 /μ были фиксированными и равными
7 и 104 соответственно. ЧислаГрасгофа и Бингама варьировались. Вязкопластическое поведение жидкости можно характери-
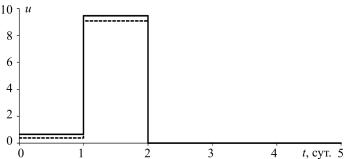
зовать так называемым числом Бингама: Bn = (τ0 / μ) L / (gβ T ) .
Известно, что при малых напряжениях сдвига вязкопластическая жидкость не течет. При фиксированном числе Грасгофа конвективное течение в замкнутой области при нагреве сбоку возникает,
488
если число Бингама меньше некоторого критического значения, зависящего от геометрии области [2–3].
На рис. 1 приведены изолинии температуры, функции тока,
профили температуры и |
вертикальной |
компоненты |
скорости |
в горизонтальном сечении, |
y = H 2 при |
Gr =106 / Pr , |
Bn =10 . |
Как видно, течение имеет одновихревую структуру, имеются гидродинамические пограничные слои вблизи вертикальных границ полости, изотермы сильно искривлены. Профиль температуры значительно отличается от линейного профиля, соответствующего теплопроводному режиму, на профиле вертикальной компоненты скорости видны пограничные слои вблизи твердых границ и участкиплато, характерныедлявязкопластических жидкостей.
На рис. 2 аналогичные результаты представлены для Bn = 30 . Для жидкости Бингама при Bn, больших некоторого
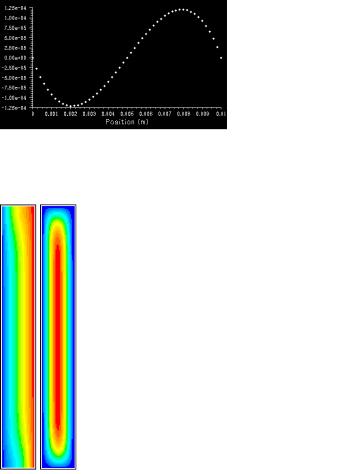
Рис. 2. Поля температуры, функции тока (слева), профили температуры (справа вверху) и вертикальной компоненты скорости (справа внизу) в горизонтальном сечении, y = H / 2
для жидкости Хершеля–Балкли при Pr = 7, Ra = 106 , Bn = 30
значения, течение должно отсутствовать. Для жидкости Херше- ля–Балкли движение не может полностью отсутствовать, но оно должно быть слабым. Как видно, интенсивность движения действительно мала: она на порядок меньше, чем при том же числе Грасгофа для Bn =10 . Поле температуры близко к теплопроводному, профиль температуры близок к линейному, а профиль вертикальной компоненты скорости – к кубическому профилю.
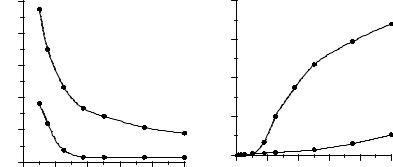
Приведенные выше результаты иллюстрируются также рис. 3 и 4, на которых приведены зависимости максимального значения функции тока в полости от числа Бингама при числах Грасгофа, равных 106 / Pr, 105 / Pr , и от числа Грасгофа при числах Бингама, равных 10 и 25.
0.02 |
|
|
|
|
|
max |
|
|
|
|
|
016 |
|
|
|
|
|
0.012 |
|
|
|
|
|
0.008 |
|
|
|
|
|
0.004 |
|
|
|
|
|
0 |
|
|
|
|
|
0 |
20 |
40 |
60 |
80 |
Bn 100 |
Рис. 3. Зависимости максимального значения функции тока в полости от числа Бингама для жидкости Хершеля–
Балкли при Ra = 106 , 105 (пустые
и заполненные окружности соответственно)
0.008 |
|
|
|
|
|
max |
|
|
|
|
|
.006 |
|
|
|
|
|
0.004 |
|
|
|
|
|
0.002 |
|
|
|
|
|
0 |
|
|
|
|
|
0 |
40000 |
80000 |
120000 |
160000 |
200000 |
|
|
|
|
|
Gr |
Рис. 4. Зависимости максимального значения функции тока в полости от числа Грасгофа для жидкости Хершеля–Балкли при Bn=10 и 25 (пустые и заполненные окружности соответственно)
Работа выполнена при финансовой поддержке Российского научного фонда (грант 14-01-00090).