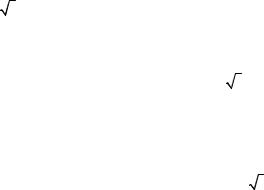Математическое моделирование в естественных науках

наглядно представить и оценить эффекты сложного нагружения представительного макрообъема (макрообразца), получить количественные оценки запаздывания векторных и изменения скалярных свойств при произвольном сложном нагружении реальных деталей и конструкций. Известные авторам эксперименты на сложное нагружение (двухзвенные траектории с изломом) тонкостенных трубчатых образцов ограничены малыми полными деформациями (на сдвиг – не более 5 %).

Следует отметить, что постановка эксперимента в случае больших градиентов перемещений связана с некоторыми сложностями, а именно с потребностью введения подвижной системы координат, связанной с материалом. Необходимость введения такой системы координат обусловлена, во-первых, тем, что образ процесса должен описывать свойства исследуемого материала и поэтому должен рассматриваться в системе координат, связанной с деформируемым материалом; во-вторых, требованием выполнения принципа независимости образа процесса от наложенного жесткого движения. В связи с этим построение образа процесса нагружения и проверку постулата изотропии необходимо проводить в подвижной системе координат, отвечающей за квазитвердое движение представительного объема.

В ходе работы получены численные результаты нагружения представительного объема поликристалла стали 45 по траекториям с изломом в случае больших градиентов перемещений. Полученные результаты свидетельствуют о хорошем согласовании с экспериментальными данными. Также получены результаты нагружения по различным траекториям в случае больших градиентов перемещений.

Работа выполнена при поддержке гранта Правительства Российской Федерации (Постановление № 220 от 9 апреля 2010 г., договор № 14.В25.310006 от 24 июня 2013 года) и Российского фонда фундаментальных исследований (гранты № 14-01-00069-а,

№ 14-01-96008 р_урал_а).

511

КРИТЕРИЙ ДОСТОВЕРНОСТИ ВЫБОРА ЗАКОНА РАСПРЕДЕЛЕНИЯ ПРИ МОДЕЛИРОВАНИИ ПРОЦЕССА БИОЛОГИЧЕСКОЙ ДЕСТРУКЦИИ

А.А. Баранова1, А.А. Селянинов1, Е.В. Вихарева2

(1Пермский национальный исследовательский политехнический университет,

Пермь, Россия, aabaranova20@gmail.com,

2Пермская государственная фармацевтическая академия,

Пермь, Россия, vihareva@pfa.ru)

Рассматривается вопрос, связанный с выбором достоверного закона распределения системы случайных величин при малом объеме выборки. В качестве критерия предложена дисперсия случайного процесса, возможность применения которой подтверждается данными эксперимента. В результате система случайных величин характеризуется логнормальным законом распределения, с применением которого определены основные числовые характеристики повторяемости процесса и область течения реализаций с заявленной вероятностью.

Ключевые слова: критерий достоверного закона распределения, числовые характеристики случайного процесса, повторяемость биологической деструкции.

Работа посвящена исследованию повторяемости процесса биологической деструкции дротаверина гидрохлорида [1]. Основным является вопрос о достоверности гипотезы распределения системы случайных величин, так как этот закон является определяющим. В условиях малого объема выборки произвели выбор критерия для определения достоверного закона распределения системы случайных величин на основе анализа сходимости основных числовых характеристик случайного процесса: математического ожидания mх (t) и дисперсии Dх (t).

При уменьшении дисперсий случайных величин в рассматриваемых подходах наблюдается тенденция сходимости результатов по математическому ожиданию и дисперсии случайного процесса. При этом скорость сходимости кривых для математического ожидания значительно выше, чем кривых для дисперсий, поэтому в качестве критерия достоверного закона

512

распределения системы случайных величин была выбрана дисперсия случайного процесса Dх (t) как наиболее чувствительная к исходным дисперсиям Da и Db характеристика.

Введенныйкритерий– дисперсияслучайногопроцесса– Dx (t) применили для выбора достоверного закона распределения системы случайных величин. Для этого представили случайный процесс как систему случайных величин, полученных в сечениях процесса по времени, для которых по экспериментальным данным нашли дисперсии в соответствующие моменты времени в условиях малого объема выборки [4] (рис. 1).

Рис. Дисперсия процесса биологической деструкции дротаверина гидрохлорида: 1 – нормальный закон распределения; 2 – линеаризация; 3 – логнормальный закон распределения; -•- – экспериментальные значения;

‒▪‒– значения по кинетическим кривым

Из рисунка следует, что дисперсия процесса по данным эксперимента близка к дисперсии, определенной с применением гипотезы о логнормальном законе распределения, поэтому его можно использовать для анализа случайного процесса биологической деструкции дротаверина гидрохлорида.

513

Список литературы

1.Стохастический анализ повторяемости процесса биодеструкции дротаверина гидрохлорида / А.А. Селянинов, Е.В. Вихарева, И.Б. Ившина, А.А. Баранова, Ю.Н. Карпенко // Россий-

ский журнал биомеханики. – 2013. – Т. 17, № 1 (59). – С. 41–54.

2.Гмурман Е.В. Теория вероятностей и математическая статистика. – М.: Высшая школа, 1997. – 479 с.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ДИФФУЗИИ ХРОМА В СПЕЧЕННЫХ ПОРОШКОВЫХ СТАЛЯХ

Н.А. Булычева, В.И. Кочуров, И.Ю. Зубко

(Пермский национальный исследовательский политехнический университет,

Пермь, Россия, zoubko@list.ru)

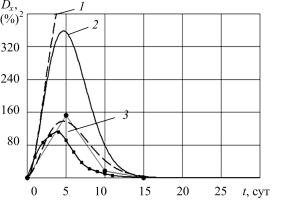
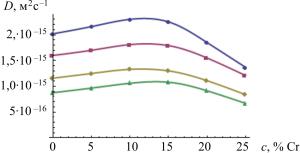
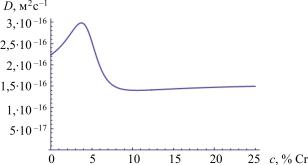
В работе для моделирования процесса диффузии при спекании порошковых сталей на основе железа, легированных хромом, разрабатывается набор правил метода клеточных автоматов, позволяющих исследовать процессы диффузии хрома в железе при заданной температуре, когда коэффициент диффузии зависит от концентрации вещества. Метод клеточных автоматов позволяет исследовать произвольную геометрию границ между частицами порошка, допускает эффективное применение высокопроизводительных многопроцессорных вычислений. Для разработки модели диффузии на основе метода клеточных автоматов проведен анализ уравнений диффузии в бинарной системе с переменным коэффициентом диффузии, зависящим от концентрации примеси. Для модификации правил автомата с учетом влияния концентрации на коэффициент диффузии выполнена обработка известных экспериментальных данных о диффузии хрома в железе.

Ключевые слова: переменный коэффициент диффузии, метод клеточных автоматов, диффузия хрома в железе, спеченные порошковые стали.

Исследуется процесс диффузии легирующих добавок хрома в системах на основе железа, получаемых в результате холодного и теплого прессования смеси частиц порошка распы-

514

ленного железа АНС 100.29 и нержавеющей стали 304L (содержит 18 % хрома и 12 % никеля) при последующем спекании с инфильтрацией расплавом меди. Частицы нержавеющей стали являются источником легирующих элементов (хром и никель), перераспределяющихся в результате диффузионного спекания по объему образца. Медь, занимающая после инфильтрации часть порового пространства, также перераспределяется за счет диффузии по объему тела. Основными задачами данного исследования являются определение конечной равновесной концентрации легирующих элементов в объеме спеченного образца и времени, за которое может быть достигнуто распределение примеси, близкое к равновесному состоянию.

При моделировании диффузии в исследуемой системе рассматривается «осредненная» частица железа, «осредненная» частица нержавеющей стали и «осредненная» прослойка между ними. Осреднение здесь производится по реализациям состояния соответствующих частиц в данном образце в течение всего процесса спекания. Прослойка вводится для передачи диффузионных потоков хрома (и впоследствии никеля) от частиц нержавеющей стали к частицам железа. Для упрощения модели принимается, что осредненные частицы порошка имеют форму, близкую к сферической, и эта форма сохраняется при спекании. Также принимается, что прослойка между частицами всегда однородна, мгновенно передает диффузионный поток от частицы к частице, и ее массовая доля в образце мала. Отметим, что в реальности существуют частицы железа и нержавеющей стали, имеющие непосредственный контакт, через область которого диффузия будет происходить быстрее, и симметрия распределения диффундирующих элементов для таких частиц будет отличаться от сферической. Для учета подобных деталей необходимо решать задачу о диффузии с заданием реального пространственного распределения частиц, пор, включений меди, образовавшихся после инфильтрации. Но для получения приближенных инженерных оценок времени перераспределения

515

легирующих элементов и их равновесной концентрации этими структурными элементами можно пренебречь. Отметим также, что при учете реального пространственного расположения всех элементов структуры и формы частиц вид напряженного состояния в них может отличаться от гидростатического. В таком случае напряжения могут влиять на диффузию. Оценка реального поля напряжений в частицах представляется избыточной для данного исследования задачей, способной дать лишь незначительное уточнение времени установления равновесной концентрации, но приводящей к существенному усложнению модели. Поэтому, переходя к исследованию осредненного состояния всех частиц, будем считать, что напряженное состояние в частицах является гидростатическим и однородным по образцу, т.е. на процесс диффузии не влияет. Также не учитывается влияние деформации решетки и периода кристаллической решетки на процесс взаимной диффузии компонентов сплава, которое для большинства металлических систем мало [1].

Далее рассмотрим диффузию хрома из частицы нержавеющей стали в частицу чистого железа. В ряде экспериментальных работ отмечается, что присутствие никеля не оказывает влияния на коэффициент диффузии хрома в железе [1]. Поэтому дополним набор принятых допущений предположением, что процессы перераспределения хрома и никеля в рассматриваемой системе можно исследовать независимо.

Принимается, что коэффициент диффузии D зависит от концентрации диффундирующего элемента c, что подтверждается в экспериментальных исследованиях, обсуждаемых, например, в работах [1–5], поэтому в качестве основного рассматривается уравнение диффузии с коэффициентом взаимной диффузии компонентов, зависящим от концентрации, т.е. D = D(c) , где c –

концентрация легирующего элемента:

∂c = (D(c) c) ,

∂t

516

В силу принятых гипотез рассматривается процесс радиальной диффузии в частицах, т.е. исследуемая концентрация является функцией времени t и одной пространственной переменной – радиуса r, отсчитываемого от центра частицы c = c(r,t). Тогда урав-

нениедиффузии(1) в частицахпринимает вид:

Для численного решения уравнения (2) требуется задать вид функции D(c) . При экспериментальном определении этой

функции используется решение, полученное с помощью подхода Больцмана–Матано [1]. Для этого к одномерному уравнению диффузии с переменным коэффициентом диффузии, записанному в декартовой системе координат, применяется подстановка

λ = r / 2 t. В рассматриваемом случае частиц со сферической симметрией частные производные λ по r и t равны выражениям:

Следовательно, производные от концентрации c представляются в виде:

Подставляя полученные производные в уравнение диффузии, получим

517

Из приведенного уравнения может быть исключено время t:

Преобразованное уравнение (3) в отличие от уравнения в частных производных (2) является обыкновенным дифференциальным уравнением, и его численное решение может быть получено более простыми методами.

В работе [6] разработана методика определения коэффициента D(c) по кривой распределения концентрации для одно-

мерной диффузии через плоскую поверхность. Здесь рассматривается сферическая поверхность частиц, и применять эту методику для анализа кривой распределения концентрации в таких частицах нельзя. Методика [6] может быть обобщена с помощью (4) на случай диффузии в шаровых частицах. Далее эта задача в работе не исследуется.

Поскольку коэффициент диффузии D характеризует интенсивность процесса перераспределения компонентов сплава, то зависимость D(c) от концентрации примеси является универ-

сальной и не зависит от геометрии тела. Таким образом, если эта функция определена с помощью стандартной методики для образца с плоской поверхностью, то ее можно использовать и при решении задачи о диффузии для тел с произвольными криволинейными поверхностями. В работе [3] приведены результаты экспериментального определения зависимости коэффициента взаимной диффузии в системе Fe–Cr для различных значений кон-

518

центрации хрома в широком диапазоне температур. Часть представленных экспериментальных данных для различных значений температуры в графическом виде приведена на рис. 1.

Рис. 1. Зависимость [3] коэффициента взаимной диффузии D (c) от концентрации хрома

в системе Fe–Cr для разных температур

Приведенные экспериментальные зависимости для каждого значения температуры описываются с помощью Паде-аппро- ксимации соотношениями

которые содержат 6 неизвестных коэффициентов, однозначно определяемых по шести экспериментальным точкам для любого

Для широкого диапазона температур в результате обработки данных экспериментальных исследований [3] получена зависимость коэффициента диффузии хрома в железе от его

519

концентрации и температуры, справедливая для малых и средних значений концентрации хрома (не более 0,25):

где экспоненциальный множитель преобразован за счет подстановки точного значения универсальной газовой постоянной R. Как видно, этот множитель также зависит от концентрации хрома. Температура является абсолютной.

Рис. 2. Зависимость коэффициента диффузии хрома в железе от концентрации хрома при абсолютной температуре T = 1423 ± 50 K

В процессе спекания при температуре T = 1423 ± 50 K получиминтервал изменения коэффициентадиффузии хромав железе:

D [1,40×10−16 ; 2,98×10−16 ] (м2 с–1).

Графически зависимость коэффициента диффузии хрома в железе при температуре T = 1423 ± 50 представлена на рис. 2. Она имеет локальные максимум и минимум внутри интервала изменения концентрации хрома.

Для описания диффузии через криволинейную поверхность вместо решения уравнения (2) или (4) применен метод

520