Математическое моделирование в естественных науках

• η – величина коэффициента влияния памяти вещества, принимающая значения ηa – низкая, ηb – высокая.

Функции принадлежности всех нечетких множеств зада-

ны в [4].

Задаем лингвистические правила в следующем виде: если разница средней по времени температуры и текущей температуры αe очень высокая и влияние памяти ηb высокое, тогда необходимо изменить текущую температуру на величину αe с учетом знака. Все правила перечислены в [4].

С помощью логических операций правила записываются

в следующем виде: ek ,l ,malt,i , j ηm → akt+,i , jt . l ,m

Для численного расчета строим вспомогательную векторную функцию:

Четкое значение добавочного вклада памяти в температуру ячейки с номерами i, j находится центроидным методом:

Tmin

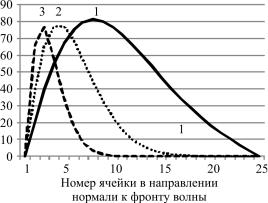
Построим для сравнения профили волны в квазилинейной среде с гармоническим граничным условием

τti ,0 = τmax (0,5 – 0,5cos(0,02 t )) при L = 1, L = 2, L = 5 и

ξ = 100.

Из рисунка видно, что наличие памяти делает систему более инерционной.

401

2006. – URL: https: //www.wolframscience.com/conference/2006/presentations/materials/alonsosanz.pdf (accessed: 09.02.2015).

4.Марценюк М.А., Селетков И.П. Нечеткий клеточный автомат для регулирования поля температуры // Научно-техни- ческие ведомости СПбГПУ. Информатика. Телекоммуникации. Управление. – СПб.: Изд-во Политехн. ун-та, 2015. – № 2–3 (217–222). (В редакции).

5.Giorgi C., Grandi D., Pata V. On the Green-Naghdi Type III Heat Conduction Model // Mathematics Subject Classification. – 2000.

6.Ковалев В.А., Радаев Ю.Н., Семенов Д.А. Связанные динамические задачи гиперболической термоупругости // Изв. Сарат. ун-та. Сер.: Математика. Механика. Информатика. – 2009. – Т. 9, вып. 4 (2). – С. 94–127.

7.Самарский А.А., Николаев Е.С. Методы решения сеточных уравнений. – М.: Наука, 1978. – 592 с.

8.Галлагер Р. Метод конечных элементов. Основы. – М.:

Мир, 1984.

ВЛИЯНИЕ РАЗМЕРА ЗЕРНА НА ПРЕДЕЛ ТЕКУЧЕСТИ В ДВУХУРОВНЕВОЙ МОДЕЛИ ДЕФОРМИРОВАНИЯ ПОЛИКРИСТАЛЛА

Д.Г. Селуков1, П.С. Волегов2

(Пермский национальный исследовательский политехнический университет,

Пермь, Россия, 1siluk94 @mail.ru, 2crocinc@mail.ru)

Рассмотрена и реализована двухуровневая модель деформирования поликристалла, учитывающая зернограничное упрочнение. Проведена идентификация и верификация внутренних параметров модели для технически чистой меди. Проведены численные эксперименты, демонстрирующие влияние в рамках модели размера зерна на предел текучести поликристалла меди.

Ключевые слова: многоуровневые конститутивные модели, физические теории пластичности, закон Холла-Петча, зернограничное упрочнение.

403

Металлы широко используются по всему миру, изучение их свойств ведется с давних пор и продолжается по сей день. Существует множество способов обработки металлов, широко распространена обработка давлением, т.е. путем пластических деформаций. К таким методам относятся прокатка, прессование, волочение, штамповка и др. Известно, что реализация пластических деформаций в кристаллах осуществляется за счет движения дислокаций по системам скольжения. Такой механизм деформации сам по себе влечет другие эффекты, основанные на взаимодействии дислокаций друг с другом и другими дефектами кристаллических решеток, например: границами зерен в поликристалле, точечными дефектами. Поэтому учет движения дислокаций в моделях неупругого деформированиявполне логичен и важен.

В работе рассматривается двухуровневая модель, состоящая из элементов макро- и мезоуровней [1], соответствующих масштабам представительных объемов поликристалла и отдельного зерна. Введение масштабов позволяет внести в модель описание основного механизма пластической деформации кристаллов путем рассмотрения сдвигов по системам скольжения кристаллитов. Активация систем скольжения происходит при достижении на них касательными напряжениями критических значений. Явление упрочнения описывается путем введения эволюционных уравнений для критических касательных напряжений, которые учитывают различные механизмы упрочнения, например: упрочнение, связанное со взаимодействием одиночных дислокаций и дислокаций леса, зернограничное упрочнение. При этом механизмы упрочнения считаются независимыми и их совместное действие описывается выражением (1):

404

Слагаемое, отвечающее за зернограничное упрочнение, принято в виде [2–5]:

где η – параметр зернограничного упрочнения; d – средний размер зерна; γ(i), γ(i) – сдвиги по системам скольжения и их скорости соответственно; K – количество соседних зерен для данного;

M(i)(l ) – мера взаимной разориентации данного зерна, соседнего (l-го) зерна (i-й системы скольжения с системами скольжения соседнего зерна) и границы; S (l) – площадь соприкосновения l-го зерна с данным; S – площадь поверхности, соприкасающейся с соседними зернами.

Мера разориентации принимается, исходя из согласованности пластических деформаций соседних зерен [2–5]. Она заключается в выборе системы скольжения соседнего зерна, при активации которой пластический сдвиг будет наиболее близким к сдвигу по текущей системескольжениятекущего зерна по некоторой мере.

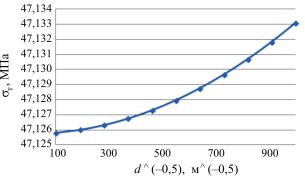
В работе была рассмотрена и реализована двухуровневая модель неупругого деформирования поликристалла. На рисунке представлена зависимость предела текучести от размера зерна

Рис. Влияние размера зерна на условный предел текучести σ0,2

405

поликристалла меди, состоящего из 373 зерен фиксированной случайной равномерно распределенной ориентации при варьировании размера зерна в диапазоне 1–100 мкм.

Данный результат близок к соотношению Холла–Петча, при котором кривая на вышеуказанном рисунке должна быть линейной.

Работа выполнена при поддержке гранта Президента РФ № МК-4917.2015.1, гранта Российского фонда фундаментальных исследований № 14-01-96008 р_урал_а.

Список литературы

1.Трусов П.В., Волегов П.С., Кондратьев Н.С. Физические теории пластичности: учеб. пособие. – Пермь: Изд-во Перм. нац. исслед. политехн. ун-та, 2013. – 244 с.

2.Трусов П.В., Волегов П.С. Физические теории пластичности: приложение к описанию упрочнения в поликристаллах // Вестник Тамбов. ун-та. Сер.: Естественные и технические нау-

ки. –2010. – Т. 15, № 3–1. – С. 983–984.

3.Трусов П.В., Волегов П.С., Янц А.Ю. Описание внутризеренного и зернограничного упрочнения моно- и поликристаллов // Науч.-техн. ведомости С.-Петербург. гос. политехн. ун-та. Физико-математические науки. – 2010. – Т. 2, № 98. – С. 110–119.

4.Кондратьев Н.С., Трусов П.В. О мере разориентации систем скольжения соседних кристаллитов в поликристаллическом агрегате // Вестник Пермского национального исследовательского политехнического университета. Механика. – 2012. –

№2. – С. 112–127.

5.Кондратьев Н.С., Трусов П.В. Описание упрочнения систем дислокационного скольжения за счет границ кристаллитов в поликристаллическом агрегате // Вестник Пермского национального исследовательского политехнического университета.

Механика. – 2012. – № 3. – С. 78–97.

406

НЕКОТОРЫЕ КАЧЕСТВЕННЫЕ СВОЙСТВА РЕШЕНИЙ ЗАДАЧИ О ПОЛЗУЧЕСТИ ДЛЯ ОДНОЙ ДРОБНОЙ РЕОЛОГИЧЕСКОЙ МОДЕЛИ ДЕФОРМИРУЕМОГО ТВЕРДОГО ТЕЛА

Е.М. Сергеева

(Самарский государственный технический университет,

Самара, Россия, sergeeva-lena93@mail.ru)

Предложена математическая модель вязкоупругих сред с памятью, основанная на замене целочисленных производных линейными выпуклыми оболочками дробных операторов Римана–Лиувилля. Найдены аналитические решения задачи о ползучести в стадии нагружения для аналогов моделей Фойхта и Максвелла. Проведен качественный сравнительный анализ найденных решений задачи о ползучести с решениями, полученными на основании изученных ранее дробных аналогов соответствующих реологических моделей, изучена асимптотика решений.

Ключевые слова: математические модели вязкоупругих сред с памятью, ползучесть, дробные операторы Римана–Лиувилля, дробные дифференциальные и интегральные уравнения, линейная выпуклая оболочка операторов, специальные функции типа Миттаг−Леффлера

иих асимптотики.

Вработе [1] предложена одномерная обобщенная модель вязкоупругого тела с памятью:

мент времени t; ak ,bk , E0 − заданные постоянные величины; D0αt φ = (d / dt)n I0nt−αφ− левосторонняя дробная производная Ри-

Лиувилля порядка β > 0 [2]. Если αk ,βk = k (k N) , то соотношение (1) превращается в стандартную обобщенную модель

407

вязкоупругого тела, частными случаями которой являются законы Гука и Ньютона, классические реологические соотношения Фойхта, Максвелла, Кельвина и др. Ясно, что переход от классической модели к ее дробному аналогу фактически осуществляется путем замены целочисленных производных дробными производными. Такой подход часто используется в задачах математического моделирования различных процессов и явлений в механике, физике, биологии и других науках [3]. В монографии [2] отмечается, что многие авторы используют в равенстве

(1) некоторый оператор дифференцирования Dα, представляющий собой «подходящую дробную производную», в качестве которой выбирается производная по Капуто. В действительности в математических моделях вязкоупругого тела, опирающихся на принцип наследственности Вольтерры, возникают интегральные операторы с ядрами абелевского типа, которые записываются в терминах дробного интеграла Римана–Лиувилля. Производные по времени от этих дробных интегралов являются дробными производными Римана–Лиувилля.

В работе [4] была предложена математическая модель вязкоупругого поведения деформируемого твердого тела на основе оператора qD0nt−α + (1− q)D0nt+α , являющегося линейной вы-

пуклой оболочкой двух производных, дробный порядок которых отклоняется от некоторого целочисленного значения на величину ±α, α [0,1/ 2) , q [0,1]. В работе [5] найдено явное реше-

ние задачи о ползучести для соответствующего дробного аналога реологической модели Фойхта, а в работе [6] изучены дробные аналоги реологических моделей Фойхта и Максвелла и обоснована непрерывная зависимость найденных решений от параметра α. Показано, что при α → 0 найденные решения переходят в хорошо известные классические решения задачи

оползучести при σ = σ0 = const.

Внастоящей работе изучены асимптотические свойства аналогов реологических моделей Фойхта и Максвелла на основе известных асимптотик функции типа Миттаг−Леффлера

408

В качестве примера рассмотрим дробный аналог модели Максвелла. Определяющее соотношение в рамках предложенной концепции записывается в виде:

ференциальное уравнение дробного порядка (3) с начальным

условием lim u(t) = 0 редуцируется к интегро-дифференциаль-

t→0+

ному уравнению:

для любой суммируемой функции σ(t) . Для закона нагружения σ = σ0 = const решение интегро-дифференциального уравнения

(4) находится в явном виде, откуда

409

где Exp(α,μ;λ;t) = tμ−1Eα (λtα;μ) −обобщенная дробная экспоненциальная функция [8], λ = q / (1− q) < 0; E0 ,η− определенные

константы модели.

Ограничиваясь в формуле (2), случаем p = 1; нетрудно

получить соответствующую асимптотическую формулу для дробной экспоненциальной функции:

Хорошо известно, что решение задачи о ползучести при σ = σ0 = const в соответствии с определяющим соотношением в рамках математической модели (1)

E0σ(t) + ηD0αt σ(t) = ηE0 D0αt ε(t)

Легко заметить, что закон изменения деформации (5) при α → 0 и закон изменения деформации (7) при α → 1 переходят в известную формулу ползучести в рамках классической модели Максвелла. Наличие дополнительного параметра q в математической модели (3) и асимптотической формуле (6) представляет интерес с точки зрения повышения точности аппроксимации экспериментальных данных.

410