
Математическое моделирование в естественных науках
..pdf
|
∂ u = − |
|
∂ p |
|
+ ν ∂2 u2 + |
∂2 u2 |
+ |
∂2 u2 |
, |
|
|
||||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
∂ t |
|
ρ∂ x |
∂ x |
|
|
∂ y |
|
|
∂ z |
|
|
|
|
|||||||||
|
∂ v = − |
|
∂ p |
+ ν ∂2 v2 + |
∂2 v2 |
+ |
∂2 v2 |
, |
|
|
|||||||||||||
|
|
|
|
|
|
||||||||||||||||||
|
∂ t |
|
ρ∂ y |
∂ x |
|
|
∂ y |
|
|
∂ z |
|
|
|
(1) |
|||||||||
∂ w = − |
∂ p |
+ ν ∂2 w2 + |
∂2 w2 + |
∂2 w2 , |
∂ u + |
∂ v + |
∂ w = 0, |
||||||||||||||||
|
|||||||||||||||||||||||
|
|
||||||||||||||||||||||
∂ t |
ρ∂ z |
∂ x |
∂ y |
∂ z |
|
|
∂ x |
|
∂ y |
∂ x |
|
||||||||||||
|
∂T + w |
d T0 |
= χ ∂2 T2 + |
∂2 T2 |
+ |
∂2 T2 |
. |
|
|
||||||||||||||
|
|
|
|
||||||||||||||||||||
|
∂ t |
|
|
d z |
∂ x |
|
|
∂ y |
|
|
∂ z |
|
|
|
|
||||||||
Граничныеусловиянаповерхностирасплаваz = 0 имеютвид |
|||||||||||||||||||||||
|
|
|
− p + 2νρ |
|
|
∂ |
2 |
η2 + |
∂ |
2 |
|
|
|
|
|
|
|||||||
|
|
|
∂w = σ |
|
|
η2 |
, |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
∂y |
|
∂x |
|
∂y |
|
|
|
|
|
|||||
|
|
|
∂u |
|
|
|
|
|
= ∂σ ,ρν |
|
∂v + |
∂w |
|
= ∂σ, |
|
||||||||
|
ρν |
+ ∂v |
|
|
(2) |
||||||||||||||||||
|
|
|
∂y |
|
∂x |
∂x |
|
|
∂z |
|
∂y |
|
∂y |
|
|
||||||||
|
|
|
|
|
|
|
|
∂T = 0, |
∂η = w. |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
∂z |
∂t |
|
|
|
|
|
|
|
|
|
|
|
|||
Условия прилипания и отсутствия температурных возмущений награнице «расплав – твердоетело» z = –h будут иметьвид
u = v = w = 0, T = 0. |
(3) |
Поиск решения (1)–(3) в виде бегущих волн приводит к следующему дисперсионному уравнению для полубесконечного слоя:
ω2 ((ω+ 2νk 2 )2 − 4k1k 2 ν2 + ωc2 )− |
|
−ωT2 ((1+ δ(1− k1 / k2 ))(ω2 + 2k 2 νω+ ωc2 ) − |
(4) |
−k / k2 (2kk1νω+ ωc2 )) = 0 |
|
291

где |
δ = |
ε |
; |
k |
2 |
= |
ω |
+ k |
2 ; |
k |
2 |
= |
ω |
+ k |
2 |
; |
G |
= |
dT0 |
, ω2 |
= k3σ |
0 |
/ ρ ; |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
1− ε |
|
1 |
|
ν |
|
|
|
2 |
|
χ |
|
|
|
0 |
|
dz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ωT2 = k 2σT G0 / ρ , ων = νk 2 ; ε– число Прандтля. Оно может быть сведено к алгебраическому уравнению 16-й степени. Это уравнение зависит от трех безразмерных параметров: числа Прандтля
идвух квадратов отношений частот a2 , b2 ( a = ωc / ων, b = ωT / ων ). Для малых чисел Прандтля алгебраическое уравнение распадается на два:
(z3 + z2 + 3z − 1)(z2 − 1)2 (z −1) − b2 (z2 −1)(z + 1)2 + |
|
+a2 (z2 − 1)2 − 2a2b2 = 0, |
(5) |
(z3 + z2 + 3z − 1)(z2 −1) − b2 (z − 1) + a2 (z + 1) = 0. |
|
Здесь обозначено
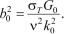 Для численных расчетов считаем, что k0 ≈ 107 м–1, h ≈ 10–5 м, G0 ≈ (Tb – Tm) /h ≈ 108 К/м, Tb, Tm – температуры плавле-
Для численных расчетов считаем, что k0 ≈ 107 м–1, h ≈ 10–5 м, G0 ≈ (Tb – Tm) /h ≈ 108 К/м, Tb, Tm – температуры плавле-
ния и кипения.
Результаты расчетов для железа приведены на рис. 1 и 2. На рис. 1 представлена зависимость безразмерного декремента от волнового числа. Максимум инкремента приходится на волновое число 5,61·107 м–1, что соответсвует длине волны 112 нм. Эти значения несколько отличаются от экпериментальных значений*. Однаков данной работе исследовалась матенситная сталь, а, как известно, углерод оказывает влияние на поверхностное натяжение железа. С ростом градиента температуры значения волнового числа резко возрастают (см. рис. 2), достигая при толщине жидкого слоя 100 нм значения 1,29·105 м–1, что
соответсвует длине волны 4,86 нм.
* Cтруктура и свойства износостойкой наплавки на сталь Xардокс 400 / Е.В. Капралов, Е.А. Будовских, В.Е. Громов, С.В. Райков, А.М. Глезер, Ю.Ф. Иванов // Проблемы черной металлургии и материаловедения. 2015. № 1. С. 80–86.
292
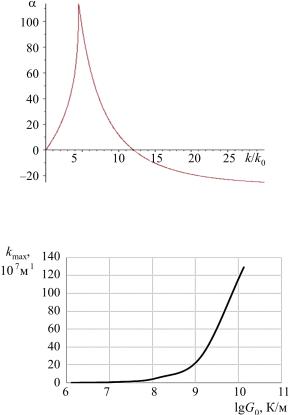
Рис. 1. Зависимость безразмерного декремента от волнового числа
Рис. 2. Зависимость волнового числа от градиента температуры
Таким образом, представлена математическая модель формирования наноструктур на поверхности наплавляемого металла. Наноструктуры образуются в результате термокапиллярной неустойчивости.
Исследование выполнено за счет гранта Российского научного фонда (проект № 15-19-00065).
293
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ВЗАИМОДЕЙСТВИЙ НЕФТЕОКИСЛЯЮЩИХ АКТИНОБАКТЕРИЙ
В ЛАБОРАТОРНЫХ АССОЦИАЦИЯХ
Д.Г. Некрасов1, Д.А. Дзюба2, И.Б. Ившина2,3, М.С. Куюкина1,2,3, М.А. Осипенко1
(1Пермский национальный исследовательский политехнический университет,
Пермь, Россия, oma@theormech.pstu.ac.ru,
2Пермский государственный национальный исследовательский университет,
Пермь, Россия, kuyukina@iegm.ru,
3Институт экологии и генетики микроорганизмов УрО РАН,
Пермь, Россия, kuyukina@iegm.ru)
Рассматривается математическая модель взаимодействия бактериальных культур в синтетическом сообществе. Известные качественные представления о возможных видах взаимодействий дополнены количественным описанием с помощью коэффициентов взаимодействия. Построенная математическая модель сопоставлена с экспериментальными даннымии полученытеоретическиезначенияэтихкоэффициентов.
Ключевые слова: синтетические микробные сообщества, межвидовые взаимодействия, коэффициенты взаимовлияния, математическая модель, метод наименьших квадратов, нормальное решение.
Для преодоления трудностей в изучении естественных микробных сообществ современные исследователи предлагают использовать искусственные или синтетические микробные сообщества (лабораторные ассоциации), проявляющие ключевые свойства их естественных аналогов. Такие синтетические микробные сообщества могут служить модельными системами, позволяющими оценить ключевые экологические, структурные и функциональные свойства микробных сообществ в контролируемых условиях. Один из подходов к изучению синтетических микробных сообществ основан на изучении межвидовых взаимодействий. Этот подход предусматривает выявление прежде всего общих схем взаимодействий между видами [1–4].
294
Эффект, оказываемый одним микроорганизмом на другой, может быть качественно оценен как нейтральный (0), позитивный (+) или негативный (–). Следовательно, возможные взаимодействия между организмами имеют следующий вид: (0, 0) – нейтральность, (0, +) – комменсализм, (0, –) – аменсализм, (+, +) – сотрудничество, (–, –) – конкуренция, (+, –) – хищничество [1].
Эти качественные оценки могут быть превращены в количественные, если ввести метаболическую активность микроорганизмов, коэффициенты их взаимодействия и сформулировать соотношения между этими величинами. Целью данной работы является построение соответствующей математической модели
исравнение ее теоретических результатов с экспериментом.
Вэксперименте, проведенном в лаборатории алканотрофных микроорганизмов ИЭГМ УрО РАН, метаболическая активность бактериальных клеток характеризовалась измеряемой посредством спектрофотометра оптической плотностью (ОП) клеточной суспензии, окрашенной йоднитротетразолем фиолетовым
ипомещенной в лунки микропланшета, в присутствии модельной нефти. Для лабораторных ассоциаций использовались штаммы пяти нефтеокисляющих актинобактерий: 1) Gordonia rubroper-
tincta ИЭГМ 124; 2) Rhodococcus opacus ИЭГМ 249; 3) Dietzia
maris ИЭГМ 302; 4) Rhodococcus ruber ИЭГМ 615; 5) Rhodococcus erythropolis ИЭГМ 767.
Коэффициенты взаимодействия штаммов kpq вводились следующим образом. Пусть ap – ОП культур бактерий, содержащих по одному виду бактерий; apq – ОП ассоциаций культур, со-
держащих по два вида бактерий; и аналогично вводятся apqr , apqrs и a12345 (пятерка культур только одна). Примем теоретическое
предположение осправедливостиследующих соотношений:
apq = ap (1+ kqp )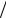 2 + aq (1+ kpq )
2 + aq (1+ kpq )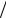 2 ,
2 ,
295
apqr = ap (1+ kqp + krp )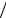 3 + aq (1+ kpq + krq )
3 + aq (1+ kpq + krq )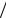 3 + ar (1+ kpr + kqr )
3 + ar (1+ kpr + kqr ) 3.
3.
и аналогичных соотношений для четверок и пятерок видов; тогда kij есть (безразмерный) коэффициент влияния i-го вида
на j-й вид.
Величины a (31 величина) измерены экспериментально. Математическая обработка этих экспериментальных данных состоит в извлечении из них величин k (20 коэффициентов). Для этого применялся метод наименьших квадратов [5] с некоторой модификацией (см. ниже). Условие минимума суммы квадратов отклонений экспериментальных значений a от теоретических приводит к системе 20 линейных алгебраических уравнений относительно коэффициентов k. Можно показать, что ранг матрицы этой системы равен 10, т.е. система имеет бесконечное (10-мер- ное) множество решений. Примем дополнительное теоретическое предположение: искомые значения k являются нормальным решением этой системы уравнений, т.е. доставляющим минимум сумме квадратов всех коэффициентов k [6].
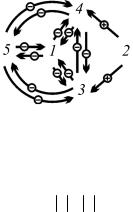
Рис. Схема взаимодействий штаммов
Знаки величин k, полученных в результате выполнения описанного алгоритма, показаны на рисунке в виде схемы взаимодействий штаммов. Если k < k средн  2 ≈ 0,1, то считалось, что взаимодействие отсутствует. Можно заметить, что преобладает конкуренция.
2 ≈ 0,1, то считалось, что взаимодействие отсутствует. Можно заметить, что преобладает конкуренция.
296
Дальнейшее исследование рассмотренной модели должно состоять в сравнении данного формального подхода к взаимодействиям актинобактерий с функциональным подходом, предусматривающим первоначальное выяснение функционального назначения сообщества с последующим описанием его структуры и динамики.
Список литературы
1.Großkopf T., Soyer O.S. Synthetic microbial communities // Curr. Opinion in Microbiol. – 2014. – Vol. 18. – P. 72–77.
2.Mitri S., Foster K.R. The genotypic view of social interac-
tions in microbial communities // Annu. Rev. Genet. – 2013. – Vol. 47. – P. 247–273.
3.Competitive and cooperative metabolic interactions in bacterial communities / S. Freilich [et al.] // Nat. Commun. – 2011. – Vol. 2. – P. 589.
4.Жукова О.В., Морозов Н.В. Исследование взаимоотношений углеводородокисляющих микроорганизмов в ассоциациях, используемых для управляемой очистки природных и сточных вод от нефтяных загрязнений // Вестник ТГГПУ. – 2007. –
№2–3, вып. 9–10. – С. 100–107.
5.Варден Б.Л. ван дер. Математическая статистика. – М.: Иностр. литература, 1960. – 434 с.
6.Калиткин Н.Н. Численные методы. – М.: Наука, 1978. –
512 с.
297
ЭВОЛЮЦИЯ ДЕФОРМИРУЕМОГО СПИРАЛЬНОГО МАГНИТНОГО ДОМЕНА В ПЕРЕМЕННОМ МАГНИТНОМ ПОЛЕ
А.А. Нестеренко, В.Н. Мальцев
(Уральский федеральный университет им. первого Президента России Б.Н. Ельцина, Екатеринбург, Россия, anna.nesterenko@urfu.ru)
В рамках феноменологической модели исследуется реализация различных сценариев существования и исчезновения спирального домена в переменном магнитном поле при деформациях формы домена. Предложена диссипативная модель спирального домена, обобщенная на случай, когда все параметры СД могут меняться со временем. Система нелинейныхуравненийдляпяти переменныхрешаласьчисленно методом Гира.
Ключевые слова: доменная структура, диссипативная модель.
При помещении пленки с перпендикулярной магнитной анизотропией в знакопеременное магнитное поле в ней формируются динамические спиральные домены (СД), которые возникают, «живут» некоторое время, а затем исчезают.
Динамические СД теоретически исследованы в работе [1], причем в гораздо меньшей степени, чем статические СД [2–5]. Основным недостатком большинства моделей как в случае динамического СД, так и в случае статических СД, является то, что варьируется только один параметр структуры при фиксированных остальных параметрах. Недостатком модели [1] является также то, что в ней исчезновение СД происходит за счет уменьшения его размера, тогда как в экспериментах такой сценарий не реализовывался.
В качестве модели был выбран одиночный СД с доменными границами, имеющими искажения в виде синусоидальной поперечной волны, представленный на рисунке. Домены с разным направлением намагниченности показаны белым и серым цветом. Намагниченность в доменах направлена перпендикулярно поверхности образца, а ширина доменной границы считается равной нулю. Это приближение справедливо для пленок с большим фактором качества.
298
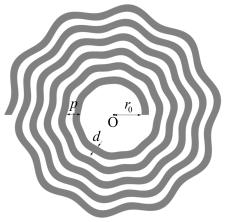
Рис. Геометрические параметры спирали
Диссипативная модель спирального домена [1] была обобщена на случай, когда могут меняться со временем все геометрические параметры СД: период спирали p; ширина домена d; радиус внутреннего ядра спирали r0; угол закрутки внешнего конца домена; амплитуда поперечных искажений формы домена. Таким образом, в данной модели рассматривалась динамика изменения формы почти свободно деформирующегося СД. Получающиеся системы уравнений решались численно методом Гира. Этот метод был выбран потому, что данные системы уравнений являются жесткими. Для исследования влияния различных деформаций формы домена на его эволюцию фиксировались некоторые его геометрические параметры и решалась система сменьшимчисломуравнений.
Модель спирального домена с учетом возможности деформации позволяет расширить набор сценариев эволюции динамического СД в переменном магнитном поле, в том числе сценариев исчезновения СД. Так, было установлено, что появление свободной области внутри СД является дестабилизирующим фактором и приводит к исчезновению домена. Данный механизм разрушения СД подтверждается результатами экспериментов [6]. Кроме того, при учете изменения ширины и периода
299
домена реализуются новые сценарии исчезновения СД за счет превращения его либо в гигантский цилиндрический домен, либо в гигантский кольцевой домен с последующим их мгновенным коллапсом. В экспериментах всегда наблюдается мгновенное исчезновение СД, имеющего конечный размер, поэтому можно полагать, что полученные в модели сценарии эволюции спиральных доменов соответствуют наблюдаемым на опыте.
Учет дополнительных деформаций домена позволяет естественным образом ввести понятие времени жизни домена как промежутка времени от начала действия поля до времени, когда домен коллапсирует. Это позволит провести дополнительные исследования зависимости этого параметра от амплитуды и частоты поля с тем, чтобы сравнить их с зависимостями, наблюдаемыми в эксперименте.
Список литературы
1.Мальцев В.Н., Кандаурова Г.С., Картагулов Л.Н. Динамическая устойчивость спирального домена в переменном маг-
нитном поле // ФТТ. – 2003. – Т. 45, № 4. – С. 658–662.
2.Борисов А.Б., Ялышев Ю.И. Магнитостатическая устойчивость спирального домена // ФММ. – 1995. – Т. 79, № 5. –
С. 18–31.
3.Ламонова К.В., Мамалуй Ю.А. Теоретическое описание спиральной доменной структуры тонких одноосных ферритгранатовых пленок // ФТВД. – 1997. – Т. 7, № 2. – С. 82–93.
4.Сойка Е.Н. Исследование гексагональной решетки спи-
ральных доменов // ФТВД. – 1998. – Т. 8, № 2. – С. 65–70.
5.Мамалуй Ю.А., Сирюк Ю.А. Влияние магнитостатического давления на условие сосуществования доменных фаз //
ФТВД. – 1999. – Т. 9, № 4. – С. 88–93.
6.Пашко А.Г. Конфигурации динамических доменных структур и процессы перемагничивания пленок ферритов-грана- тов: автореф. дис. … канд. физ.-мат. наук. – Екатеринбург, 2009. – 23 с.
300
