Уравнения поведения системы в упругой зоне определяются из условия равенства нулю перемещений со внутренней стороны цилиндра, а также выполнения условия (2) на краю зоны пластичности, и равны:
|
u = |
|
|
R2 − r2 |
|
|
|
(ν |
2 |
|
−1) |
c ρ2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
cosφ; |
(6) |
|
(ν + 1)ρ2 sin φ+ (ν−1)R2 |
|
|
E |
r |
|
|
|
|
|
|
−μR2 − r2 |
|
ρ2 |
|
|
|
|
|
|
|
|
|
|
|
|
σr = − |
|
|
|
|
|
|
|
|
|
|
|
|
ccosφ, |
(7) |
|
|
|
−μR |
2 |
+ ρ |
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
sin φ r |
|
|
|
|
|
|
|
|
|
|
|
где μ = − |
ν−1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ν+ 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнения (6)–(7) действительны в области [ρ…R]. |
|
Перемещения на краю зоны пластичности: |
|
|
up = |
|
R2 − ρ2 |
|
|
|
|
(ν |
2 |
−1) |
|
c |
|
|
|
|
|
|
ρcosφ. |
(8) |
|
(ν+ 1)ρ2 sin φ+ (ν−1)R2 |
|
|
E |
Для определения радиуса зоны пластичности воспользуемся условием непрерывности радиальных напряжений на границе пластичности.
|
|
|
p |
|
tgφ+ 1 = 1− |
|
|
μξ |
2 |
+ η |
2 |
|
sin φ |
|
sin φ |
|
|
|
|
|
|
|
|
|
|
|
η |
sin φ+1 |
, |
(9) |
|
|
|
c |
η |
2 |
sin φ− μξ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
где ξ = |
R |
, η= |
ρ |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r0 |
|
r0 |
|
|
|
|
|
|
|
|
|
|
|
|
Для упрощения решения уравнения (9) преобразуем его к следующему виду:
Ψ(τsin φ−1) + (sin φ+ 1)τ |
sin φ |
|
sin φ+1 |
= 0, |
(10) |
где
p |
|
1 |
|
|
sin φ |
|
|
sin φ+1 |
|
Ψ = |
|
tgφ+ 1 |
|
|
|
; |
|
μξ |
2 |
c |
|
|
|
|
η2 = μξ2 τ.
Уравнение (10) является двухпараметрическим от параметров Ψ и ϕ, что позволяет протабулировать его решения.
Таким образом, мы получили систему уравнений (3)–(8), позволяющую полностью описать поведение системы как в упругой зоне, так и в пластической. Уравнения (9)–(10) позволяют определить радиус зоны пластичности. При этом решение уравнения (10) может быть протабулировано, что позволит упростить прикладное решение данной задачи.
На базе УралНИИАС планируется экспериментальная проверка полученных результатов в специально созданных стальных цилиндрических камерах, заполненных грунтом, а также проведение численного моделирования в одной из систем конечноэлементного анализа.
Список литературы
1.Определение верхних оценок несущей способности фундаментов на откосах / С.А. Павлющик, В.П. Дыба, А.Н. Богомолов, Г.М. Скибин, О.А. Богомолова // Геопрофиль. – 2010. – Вып 5. –
С. 13–16.
2.Федоровский В.Г. О расширении цилиндрической скважины в упруго-пластической среде // Основания, фундаменты
имеханика грунтов. – 1972. – Вып 2. – С. 28–30.
3.Радаев Ю.Н. Пространственная задача математической теориипластичности. – Самара: Изд-воСамар. ун-та, 2006. – 340 с.
ДВУМЕРНАЯ ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ ДЕФОРМИРОВАННОГО СОСТОЯНИЯ МЕЗООБЪЕМОВ ПРИ ПЛОСКОЙ ДЕФОРМАЦИИ
А.М. Реков
(Филиал Уральского федерального университета им. первого Президента России Б.Н. Ельцина, Первоуральск, Россия)
Построена экспериментальная двумерная плотность совместного распределения показателя напряженно-деформированного состояния (НДС) и интенсивности пластических деформаций мезообъема при плоской деформации образца в пластической области. Результаты работы могут быть использованы в качестве дополнительного критерия для оценки вероятности разрушения металла при пластической деформации.
Ключевые слова: пластическая деформация, мезодеформации, аустенитная сталь, напряженно-деформированное состояние, плотность распределения.
Пластические деформации в мезоструктуре поликристалла представляют собой случайные тензорные поля. Полной характеристикой таких полей являются нормальные одномерные и двухточечные законы распределения, для определения параметров которых используется экспериментальный метод делительных сеток [1–2]. В докладе приводятся новые результаты наших исследований в данной области. Основной целью работы является построение по результатам экспериментов двумерной плотности распределения показателя напряженно-деформиро- ванного состояния и интенсивности деформаций в зернах поликристалла при плоской деформации образца. Условия плоской деформации создавали прокаткой на лабораторном стане ДУО – 120 тонких пластинок размером14×75×2 мм. Материал образцов – аустенитная сталь 12Х18Н10Т [3, 4].
Плоскости поверхности образцов притирали и полировали на шлифовальных кругах в несколько этапов с применением алмазной пасты с абразивными частицами разной крупности. Границы зерен аустенита выявляли травлением образцов в стандарт-
ных реактивах. Средний размер зерна, определенный методом случайных секущих, составил 9–11 микрометров. Делительную сетку с размерами квадратных ячеек 10 микрометров наносили фотоспособом. Для защиты сетки от истирания между образцом и валками стана прокладывали полоски тонкой бумаги.
По результатам измерений сторон ячеек делительной сетки до и после прокатки образца рассчитывали деформации в ортогональных направлениях (вдоль ε11 и поперек оси образца ε22 ), оп-
ределяли главные деформации ε1,2 и их интенсивность εи [1, 2].
εи2 = 2 (ε1 − ε2 )2 + (ε2 − ε3 )2 + (ε3 − ε1 )2 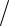 9 .
9 .
Деформированное состояние отдельных зерен оценивали с помощью случайного параметра Надаи–Лоде в мезоструктуре поликристалла [1–4]:
χ = (2ε2 − ε1 − ε3 ) / (ε1 − ε3 ).
Ниже представлена двумерная экспериментальная функция распределения f (χ,εu ) (рис. 1, в). В качестве исходных для рас-
четов принимали два массива размером 20×20 ячеек – интенсивностей деформаций и случайного параметра Надаи–Лоде в мезоструктуре. Эксперименты показывают, что интенсивность деформаций в мезоструктуре, с достаточной для практических расчетов точностью, соответствует нормальному закону. Закон распределения случайного параметра Надаи–Лоде зависит от НДС, которое реализуется в процессе деформации образца [4–6].
Коэффициент парной корреляции указанных параметров, составил величину, равную 0,19. Плотность распределения интенсивности деформаций представлена на рис. 1, а, а плотность распределения коэффициента χ – на рис. 1, б. График двумер-
ной функции распределения строили с помощью пакета прикладных программ Grapher.
Рис. 1. Плотности распределения при одноосном растяжении образца: а – интенсивность пластических деформаций; б – случайный параметр Надаи–Лоде; в – двумерное распределение интенсивности деформаций и параметра Надаи–Лоде
Координаты вершины полученного графика: среднее значение интенсивности деформаций 14,6 % – модальное значение функции распределения χ, равное нулю. Сечения поверхности плоскостями, параллельными оси χ, ограничены кривыми, подобными функции распределения параметра НДС. В сечениях плоскостями, параллельными оси εu , получаются кривые, подобные
функции распределения интенсивности деформаций (см. рис. 1, в). Авторы монографии [7] показали, что величина предельной пластичности материала в процессах обработки металлов давлением зависит от двух параметров: степени деформации сдвига и показателя напряженно-деформированного состояния. Логично предположить, что в тех зернах поликристалла, где выше степень деформации и более «жесткое» напряженно-деформированное состояние, наиболее вероятно возникновение трещин в процессе пластической
деформации.
375
Выводы
1.Построена двумерная плотность распределения интенсивности деформации и показателя напряженно-деформирован- ного состояния, отдельных мезообъемов (зерен) поликристаллического образца при плоской деформации.
2.Результаты работы могут быть использованы в качестве дополнительного критерия при анализе процессов разрушения металла.
Список литературы
1.Вайнштейн А.А., Алехин А.Н. Основы теории упругости и пластичности с учетом неоднородности материала. – Екатеринбург: Изд-во УГТУ-УПИ. 2004. – 236 с.
2.Реков А.М., Вайнштейн А.А., Березин В.В. Распределение главных микродеформаций // Вестник УГТУ-УПИ. Механика микронеоднородных материалови разрушение: сб. науч. тр. – Екатерин-
бург: Изд-воУГТУ-УПИ, 2004. – №22 (52). – С. 85–88.
3.Реков А.М. Локальные перегрузки мезоструктуры стальных образцов при плоской прокатке // Сталь. – № 11. – 2013. –
С. 90–94.
4.Плотность распределения коэффициентов поперечной деформации при плоской деформации // Математическое моделирование в естественных науках: тез. докл. XXI Всерос. школы конф. – 2012. – С. 150–151.
5.Реков А.М. Аппроксимация функции распределения случайного коэффициента Надаи – Лоде в микроструктуре // Математическое моделирование в естественных науках. – 2013. –
№1. – С. 128–130.
6.Реков А.М. Функции распределения напряженно-дефор- мированных состояний микроструктуры поликристаллов // Заводская лаборатория. Диагностика материалов. – № 2. – Т. 80. – 2014. – С. 26–31.
7.Богатов А.А., Мижирицкий О.И., Смирнов С.В. Ресурс пластичности металлов при обработке давлением. – М.: Метал-
лургия, 1984. – С. 144.
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПОЛЕТА РАКЕТЫ
Н.С. Романов
(Пермский национальный исследовательский политехнический университет,
Пермь, Россия, nikita-romanov71@rambler.ru)
Построена математическая модель полета ракеты, используемой в любительском ракетном моделизме. При моделировании учитывались процесс горения топлива, а также влияние силы сопротивления среды.
Горение топлива предполагалось равномерное. Для определения силы тяги ракетного двигателя были использованы уравнения Менде- леева–Клапейрона и химической реакции сгорания топлива.
Ключевые слова: горение, моделизм, сопротивление, движение.
Была разработана методика определения скорости горения топлива в зависимости от диаметра поперечного сечения двигателя. Для определения необходимых констант, а также для проверки адекватности гипотезы о равномерности горения топлива был проведен эксперимент.
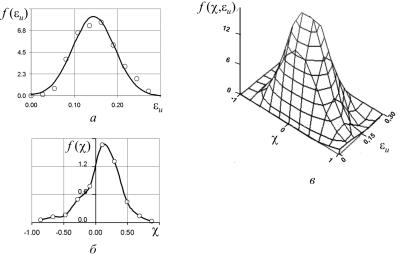
Для определения коэффициента аэродинамического сопротивления была построена аэродинамическая труба и уменьшенный макет исследуемой ракеты (рис. 1). Была разработана и применена методика определения коэффициента сопротивления по отклонению подвешенного макета в созданном установкой воздушном потоке (рис. 2).
Формула для определения коэффициента аэродинамического сопротивления:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin (α+ γ) |
|
|
|
2mg( |
|
|
cosβ− cosα) |
|
|
С = |
sin (β+ γ) |
. |
|
ρU |
2 |
S(sinα+ |
sin (α+ γ) |
|
|
|
|
|
|
|
sinβ) |
|
|
|
sin (β+ γ) |
|
Математическая модель использовала второй закон Ньютона для описания движения ракеты как материальной точки перемен-
ной массы с учетом силы сопротивления, зависящей от скорости. После нахождения параметров задачи были проведены расчеты на основании построенной математической модели с применением метода Эйлера для решения полученного дифференциального уравнения. Решение проводилосьв среде MS Excel.
Рис. 1. Моделируемая ракета и ее твердотопливный двигатель: 1 – обтекатель; 2 – верхние стабилизаторы; 3 – корпус; 4 – нижние стабилизаторы; 5 – сопло; 6 – заглушка;
7 – топливо; 8 – стенки корпуса
Рис. 2. Известные данные об испытании макета
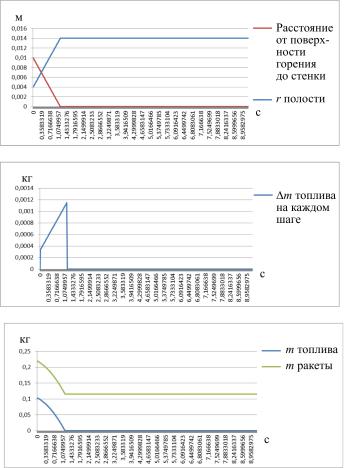
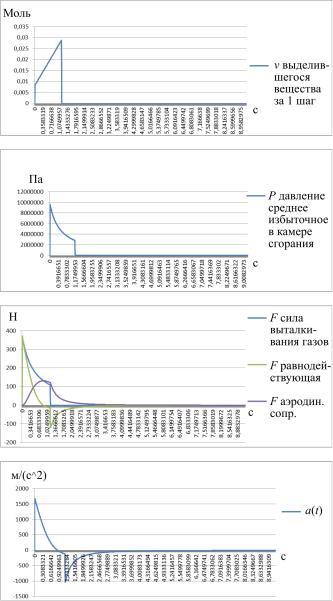
Были проведены расчеты скорости движения ракеты, ускорения, высоты подъема, избыточного давления, сил тяги и сопротивления воздуха, массы несгоревшего топлива от времени (рис. 3).
Рис. 3. Расчеты параметров ракеты


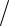 9 .
9 .