
Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического управления
.pdf
y(t) = g(x (t) u (t) t) + @g(x u t) |
|
|
x(t) + |
|
|
||||||||||||
|
|
|
|
|
@x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+@g(x u t) |
u(t) + O2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
@u |
|
|
|
|
|
|
|
|
|
|
|
|
|
£¤¥ x(t) = x(t) |
; |
x |
|
(t) { ®âª«®¥¨¥ á®áâ®ï¨ï ¨á室®© ¬®¤¥- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
«¨ ¯® ®â®è¥¨î ª ¢¥ªâ®àã x (t)\ u(t) = u(t);u (t) { ®âª«®¥- |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¨¥ ¢å®¤®£® ¯à®æ¥áá ®â u (t), @f@x( ) , |
@f@u( ) |
|
, @g@x( ) |
|
, |
@g@u( ) |
|
|
|||||||||
{ ¬ âà¨æë ç áâëå ¯à®¨§¢®¤ëå ¢¥ªâ®à-äãªæ¨© f( ) g( ) (¬ - |
|||||||||||||||||
âà¨æë ª®¡¨) ¯® ª®¬¯®¥â ¬ ¢¥ªâ®à®¢ x, u, ¢ëç¨á«¥ë¥ ¯à¨ § 票ïå x(t) x (t) u(t) u (t)\ O2 { ¬ «ë¥ ¢¥«¨ç¨ë ¢â®- ண® ¯®à浪 ¬ «®á⨠¯® x(t), u(t):
âáî¤ á«¥¤ã¥â ®¡é¨© ¢¨¤ ãà ¢¥¨© ¤«ï ¯à¨à 饨©:x(t) = A(t) x(t) + B(t) u(t) + f (t) ; x (t) + O2y(t) = C(t) x(t) + D(t) u(t) + O2
£¤¥ |
@f(x u t) |
|
@f (x u t) |
|
|
|
|
||
A(t) = |
@x |
B(t) = |
@u |
|
|
@g(x u t) |
|
@g(x u t) |
; |
C(t) = |
@x |
D(t) = |
@u |
¬ âà¨æë-äãªæ¨¨ à §¬¥à®¢ n n n m l n l m (ᮮ⢥âá⢥-
®), f (t) = f (x (t) u (t) t):
ਠ¤®áâ â®ç® ¬ «ëå ®âª«®¥¨ïå x(t), u(t) ®â ®¯®àëå âà ¥ªâ®à¨© x (t) u (t) ¬ «ë¬¨ ¢¥«¨ç¨ ¬¨ ¡®«¥¥ ¢ë᮪®£® ¯®à浪 ¬®¦® ¯à¥¥¡à¥çì.
®ªà¥âë© ¢¨¤ «¨¥ ਧ®¢ ®© ¬®¤¥«¨ § ¢¨á¨â ®â ¢ë- ¡®à ®¯®à®£® ¤¢¨¦¥¨ï x (t) u (t). ᮢ®© ¨â¥à¥á ¯à¥¤- áâ ¢«ïîâ á«¥¤ãî騥 ç áâë¥ á«ãç ¨ [23, 47, 72]:
{ ¢ ª ç¥á⢥ ®¯®à®£® ¢ë¡¨à ¥âáï ¥ª®â®à®¥ ¥¢®§¬ãé¥- ®¥ ¤¢¨¦¥¨¥, ª®£¤ x (t) u (t) 㤮¢«¥â¢®àïîâ ¨á室®¬ã ãà ¢¥¨î (1.7).
í⮬ á«ãç ¥ «¨¥ ਧ®¢ ï ¬®¤¥«ì ¨¬¥¥â ¢¨¤ |
|
x(t) = A(t) x(t) + B(t) u(t) |
|
y(t) = C (t) x(t) + D(t) u(t) |
(1.8) |
{ ¢ ª ç¥á⢥ ®¯®à®£® ¤¢¨¦¥¨ï ¢ë¡¨à îâáï ¥¨§¬¥ë¥ ¢® ¢à¥¬¥¨ á®áâ®ï¨¥ á¨áâ¥¬ë ¨ ¢å®¤®© ¯à®æ¥áá, â.¥. áç¨- â ¥âáï, çâ® x (t) 0 u (t) 0 x (t) x u (t) u (t): ®£¤
22

«¨¥ ਧ®¢ ï ¬®¤¥«ì ¨¬¥¥â ¢¨¤ |
|
x(t) = A(t) x(t) + B(t) u(t) + f (x u t) |
|
y(t) = C (t) x(t) + D(t) u(t): |
(1.9) |
¬¥â¨¬, çâ® ¢ ¯à¨¢¥¤¥ëå ¢ëè¥ á®®â®è¥¨ïå ¢ ª ç¥- á⢥ u(t) u (t) ¬®¦® а бб¬ ва¨¢ вм ¥ в®«мª® ¢¥и¨¥ ¢®§- ¤¥©бв¢¨п б¨бв¥¬г, ® ¨ ¥¥ ¯ а ¬¥вал. ®£¤ ¬®¤¥«м, ¯®«г- з¥ п ¢ а¥§г«мв в¥ «¨¥ а¨§ ж¨¨, ¯®§¢®«п¥в ¯а¨¡«¨¦¥® бг¤¨вм ® зг¢бв¢¨в¥«м®бв¨ а¥и¥¨© б¨бв¥¬л ª ®вª«®¥¨о ¯ а ¬¥ва®¢ ®в а бз¥вле § з¥¨©, ¯а¨з¥¬ нв¨ ®вª«®¥¨п ¯а¥¤бв ¢«повбп ¢ ¢¨¤¥ ¤¤¨в¨¢ле ¢®§¬гй¥¨© (в ª ª ª ®¨ п¢«повбп ª®¬¯®¥в ¬¨ "а би¨а¥®£®" ¢е®¤®£® ¯а®ж¥ббu(t)).
ਬ¥à. ¨¥ ਧ æ¨ï ¬®¤¥«¨ ¬ ï⨪«ï ¨««îáâà 樨 à áᬮâਬ «¨¥ ਧ æ¨î ãà ¢¥¨© ᢮-
¡®¤®£® ¤¢¨¦¥¨ï ¬ ⥬ â¨ç¥áª®£® ¬ ï⨪ |
|
¬ áᮩ m ¨ |
||||||||
¤«¨®© l: «¨ï¨¥¬ ᨫ âà¥¨ï ¡ã¤¥¬ ¯à¥¥¡à¥£ âì. |
«ï |
|||||||||
|
|
|
T |
£¤¥ ' |
{ 㣮« ¯®¢®à®â |
|||||
¢¥ªâ®à á®áâ®ï¨ï x(t) = ['(t) '(t)] |
|
|||||||||
¬ ï⨪ , ¯®«ã稬 á¨á⥬ã ãà ¢¥¨© |
|
|
|
|
||||||
|
x1(t) = x2(t) |
|
|
|
|
|
|
(1.10) |
||
|
x2(t) = |
|
;mglJ;1 sin(x1(t)): |
|
|
|
||||
|
|
|
|
|
|
|||||
¤¥áì J = ml2; ¬®¬¥â ¨¥à樨 ¬ ï⨪ , g; |
ã᪮२¥ ᢮- |
|||||||||
¡®¤®£® ¯ ¤¥¨ï. ã«¥¢®¬ã § 票î 㣫 |
' ᮮ⢥âáâ¢ã- |
|||||||||
¥â ¯®«®¦¥¨¥ ¬ ï⨪ |
"¢¥à⨪ «ì® ¢¨§". ï⨪ (1.10) |
|||||||||
¨¬¥¥â ¤¢ |
á®áâ®ï¨ï à ¢®¢¥á¨ï: |
x1 |
|
= 0 ¨ x2 |
= [ 0]T |
: 7 ¨- |
||||
|
|
|
|
0 |
|
|
0 |
|
|
|
¥ ਧ æ¨ï (1.10) ¢ ®ªà¥áâ®á⨠íâ¨å á®áâ®ï¨© ¯à¨¢®¤¨â ª |
||||||||||
ãà ¢¥¨ï¬ ¢¨¤ (1.3) á ¬ âà¨æ¥© |
|
|
|
|
|
|
||||
|
|
0 |
|
1 |
|
|
|
|
||
|
A = gl;1 |
0 |
|
|
|
|
||||
£¤¥ § ª "¬¨ãá" ᮮ⢥âáâ¢ã¥â |
¨¦¥¬ã, |
|
§ ª "¯«îá" { |
|||||||
¢¥à奬ã á®áâ®ï¨ï¬ à ¢®¢¥á¨ï (â.¥. â®çª ¬ x1 |
¨ x2: |
) |
||||||||
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
||||||||
7 âண® £®¢®àï, ¨¬¥¥âáï ¬®¦¥á⢮ á®áâ®ï¨© à ¢®¢¥á¨ï |
x0 = |
|||||||||
= [n 0]T |
n = : : : ; 2 ;1 0 1 2 : : : |
¯®í⮬㠤«ï § ¤ ç ¤ ®£® ⨯ |
||||||||
¯à®áâà á⢮ á®áâ®ï¨© 㤮¡¥¥ ®â®¦¤¥á⢫ïâì ¥ á ¯«®áª®áâìî R2 á ¯®¢¥àå®áâìî 樫¨¤à .
23

áᬮâਬ ⥯¥àì ¢ ª ç¥á⢥ ®¯®à®© âà ¥ªâ®à¨¨ ¯à®-
æ¥áá x (t), ã ª®â®à®£® x (t) = |
|
cos( t) x |
(t) = |
|
|
sin( t) £¤¥ |
||||
2 |
;2 |
|||||||||
|
p |
1 |
2 |
|
|
|||||
|
|
T |
|
|
|
|
|
|
||
= |
|
gl;1 |
: ¬¥â¨¬, çâ® â ª®© ¯à®æ¥áá ᮮ⢥âáâ¢ã¥â ¯®¢¥- |
|||||||
¤¥¨î ¬®¤¥«¨, ¯®«ã祮© «¨¥ ਧ 樥© ®â®á¨â¥«ì® á®-
áâ®ï¨ï x1 ¯à¨ x(0) = [ |
|
0] . ®£¤ äãªæ¨ï |
|
|
|
|||||||||||||||||
|
|
|
|
|||||||||||||||||||
|
0 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
f = h;2 |
sin( t) |
|
;mglJ;1 sin( |
2 cos( t))i |
|
: |
|||||||||||||||
á¢®î ®ç¥à¥¤ì x (t) = [ |
|
|
sin( t) |
; |
|
2 cos( t)]T ®âªã¤ |
||||||||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
; |
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|||
¯®«ãç ¥¬ ãà ¢¥¨ï ¢ ®âª«®¥¨ïå x(t) = x(t) ; x |
|
(t) : |
||||||||||||||||||||
8 |
x1 |
(t) = x2(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
x2 |
(t) = |
|
mglJ;1 cos( |
|
cos( t)) x1(t) |
|
(1.11) |
|||||||||||||||
|
|
|
||||||||||||||||||||
|
|
; |
|
|
;1 |
|
|
|
|
2 |
|
|
|
|
|
2 |
; |
|
|
|||
: |
|
; mglJ |
|
sin(2 cos( t)) + 2 |
|
cos( t): |
||||||||||||||||
< |
|
|
|
|||||||||||||||||||
à ¢¥¨ï (1.11) ¯à¥¤áâ ¢«ïîâ ᮡ®© á¨á⥬㠫¨¥©ëå ¥- ®¤®à®¤ëå ¥áâ 樮 àëå ãà ¢¥¨© ¨ ¤ îâ ¡®«¥¥ â®ç®¥ ¯à¨¡«¨¦¥¨¥ ª ª®«¥¡ ⥫쮬㠯à®æ¥ááã ¢ ¨á室®© ¥«¨- ¥©®© á¨á⥬¥ (1.10), 祬 «¨¥ ਧ æ¨ï ¢ ®ªà¥áâ®á⨠á®-
áâ®ï¨ï x01 . ⬥⨬, çâ® (1.11) ¨¬¥îâ ¢¨¤ (1.2) á® ¢å®¤ë¬ |
|||||||||||||||||
¯à®æ¥áᮬ v(t) = |
; |
mglJ;1 sin( |
|
cos( t))+ |
|
2 cos( t) ¨ ¬ âà¨- |
|||||||||||
|
|
||||||||||||||||
æ ¬¨ |
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A(t) = |
|
|
0 |
|
|
|
|
1 |
|
|
B = |
0 |
: |
||||
|
mglJ;1 cos( |
|
cos( t)) |
0 |
|
|
|
1 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
а¨¢¥¤¥ п §¤¥бм ¯а®ж¥¤га «¨¥ а¨§ ж¨¨ ¬®¦¥в ¯а¨¬¥- пвмбп (б ®з¥¢¨¤®© § ¬¥®© ®¡®§ з¥¨© ¨ а£г¬¥в®¢) ¨ ¤«п ¤¨бªа¥вле б¨бв¥¬. «п «¨¥ а¨§ ж¨¨ ª®«¥¡ в¥«мле ¯а®ж¥бб®¢ в ª¦¥ ¨§¢¥бв¥ ¨ и¨а®ª® ¨б¯®«м§г¥вбп в ª §л- ¢ ¥¬л© ¬¥â®¤ £ ମ¨ç¥áª®£® ¡ « á (£ ମ¨ç¥áª®© «¨¥ - ਧ 樨) [15, 76, 93, 94, 95, 113] (á¬. ¨¦¥ ¯. 11.3. á. 247).
1.4. ਬ¥àë ãà ¢¥¨© á®áâ®ï¨ï á¨á⥬
áᬮâਬ ¥áª®«ìª® ¯à¨¬¥à®¢ ¬®¤¥«¥© «¨¥©ëå á¨á⥬ ¢ ¢¨¤¥ ãà ¢¥¨© á®áâ®ï¨ï.
1.4.1. «¥ªâà®â¥å¨ç¥áª¨¥ ãáâனáâ¢
ਬ¥à 1. RC-楯ì. áᬮâਬ á¨á⥬ã, á®áâ®ïéãî ¨§ ¯®á«¥¤®¢ â¥«ì® á®¥¤¨¥ëå ¥¬ª®á⮣® í«¥¬¥â C ¨ १¨- áâ®à á ᮯà®â¨¢«¥¨¥¬ R (à¨á. 1.3, ). å®¤ë¬ ¯à®æ¥áᮬ
24
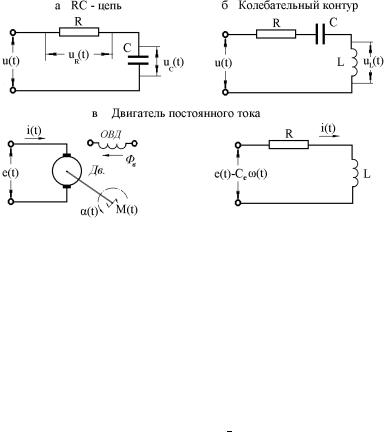
áç¨â ¥¬ ¯à殮¨¥ u(t) ®â ¢¥è¥£® ¨áâ®ç¨ª , ¯à¨«®¦¥- ®¥ ª § ¦¨¬ ¬ 楯¨. áᬮâਬ á«¥¤ãî騥 ¤¢ á«ãç ï.
¨á. 1.3. «¥ªâà®â¥å¨ç¥áª¨¥ ãáâனáâ¢
1. |
ë室 á¨á⥬ë { ¯à殮¨¥ uC(t) |
§ ¦¨¬ å ¥¬- |
ª®á⮣® í«¥¬¥â . |
|
|
RC-æ¥¯ì ®¯¨áë¢ ¥âáï ãà ¢¥¨¥¬ |
|
|
|
RCduC(t) + uC(t) = u(t): |
(1.12) |
|
dt |
|
¢¥¤¥¬ |
|
|
T = RC { ¯®áâ®ïãî ¢à¥¬¥¨ 楯¨ ¨ ¯à¨¬¥¬ x(t) = |
||
uC(t): ëà §¨¢ ¨§ (1.12) § 票¥ x(t), ¯®«ã稬 ãà ¢¥¨¥ á®- áâ®ï¨ï ¢¨¤ (1.3), ¢ ª®â®à®¬ n = 1 A = T ;1 B = T ;1 C = 1:
;
ва¨жл ¯®ап¤ª 1 1 ®¡лз® ®в®¦¤¥бв¢«повбп б® бª «па-
묨 í«¥¬¥â ¬¨, ¯®í⮬㠯ਠ¨å § ¯¨á¨ ª¢ ¤à âë¥ áª®¡ª¨ ®¯ã᪠îâáï. ©¤¥ë¥ ãà ¢¥¨ï ᮮ⢥âáâ¢ãîâ ᮡá⢥- ®© á¨á⥬¥.
2. ë室 á¨á⥬ë { ¯à殮¨¥ uR(t) § ¦¨¬ å १¨- áâ®à .
à ¢¥¨¥ á®áâ®ï¨ï (¤«ï x(t)) ¨¬¥¥â â®â ¦¥ ¢¨¤. §-
¬¥ï¥âáï ãà ¢¥¨¥ ¢ë室 , â ª ª ª ⥯¥àì y(t) = uR(t) u(t); uC(t) u(t); x(t): ®í⮬㠤 ï á¨á⥬ ¥ ®â®á¨â- áï ª áâண® ॠ«¨§ã¥¬ë¬ ¨ ¨¬¥¥â ¬ âà¨æë A = ;T;1 B =
T ;1 C = ;1 D = 1:
25

ਬ¥à 2. ®«¥¡ ⥫ìë© ª®âãà (RLC-楯ì). ¯¨è¥¬ ⥯¥àì ãà ¢¥¨ï á®áâ®ï¨ï ª®«¥¡ ⥫쮣® ª®âãà , ¢ª«î-
ç î饣® ¯®á«¥¤®¢ â¥«ì® á®¥¤¨¥ë¥ R, L, C-í«¥¬¥âë (à¨á. 1.3, ¡). ëå®¤ë¬ á¨£ «®¬ y(t) ¡ã¤¥¬ áç¨â âì ¯à殮¨¥ § ¦¨¬ å ¨¤ãªâ¨¢®£® í«¥¬¥â uL (t) ¢å®¤®¬, ª ª ¨ ¢ ¯à¥¤ë¤ã饬 á«ãç ¥, { ¯ ¤¥¨¥ ¯à殮¨ï ¢á¥© 楯¨ u(t):
ª ¨§¢¥áâ® ¨§ í«¥ªâà®â¥å¨ª¨, ¢ë¯®«¥ë á®®â®è¥¨ï
Ldi(t) = uL(t) |
CduC(t) = i(t) |
dt |
dt |
uR(t) = Ri(t) u(t) = uL(t)+uC (t)+uR(t) £¤¥ i(t) { ᨫ ⮪ ¢ æ¥- |
||||||||
¯¨, uC(t) { ¯à殮¨¥ |
§ ¦¨¬ å ¥¬ª®á⮣® í«¥¬¥â , uR(t) |
|||||||
{ ¯ ¤¥¨¥ ¯à殮¨ï |
|
ªâ¨¢®¬ ᮯà®â¨¢«¥¨¨. ¯à¥¤¥- |
||||||
|
|
|
|
|
T |
¨ ¢ë室 |
|
|
«¨¢ ¢¥ªâ®à á®áâ®ï¨ï x(t) = [i(t) uC (t)] |
|
y(t) = uL(t) |
||||||
¯®«гз¨¬ б«¥¤гойго б¨бв¥¬г га ¢¥¨©: |
|
|||||||
x1(t) = (u(t) |
; |
Rx1(t) |
; |
x2 |
(t))L;1 |
(1.13) |
||
;1 |
|
|
|
|
|
|||
x2(t) = C |
x1(t) |
|
|
|
|
|
||
y(t) = u(t) ; Rx1(t) ; x2(t): |
|
|||||||
«¥¤®¢ ⥫ì®, ¢ à áᬠâਢ ¥¬®¬ ¯à¨¬¥à¥ n = 2 m = l = 1 ¨ ãà ¢¥¨ï á®áâ®ï¨ï (1.2) ᮤ¥à¦ â ¬ âà¨æë
RL;1 |
L;1 |
B = |
L;1 |
C = [;R ;1] D = 1: |
A = ;C;1 |
; 0 |
0 |
||
ਬ¥à 3. |
¢¨£ â¥«ì ¯®áâ®ï®£® ⮪ á ¥§ ¢¨á¨- |
|||
¬ë¬ ¢®§¡ã¦¤¥¨¥¬. áᬮâਬ «¨¥ ਧ®¢ ë¥ ãà ¢¥- ¨ï í«¥ªâà¨ç¥áª®£® ¤¢¨£ â¥«ï ¯®áâ®ï®£® ⮪ á ¥§ ¢¨á¨- ¬ë¬ ¢®§¡ã¦¤¥¨¥¬ (à¨á. 1.3, ¢). ãáâì ®¡¬®âª ¢®§¡ã¦¤¥¨ï ¤¢¨£ ⥫ï ᮧ¤ ¥â ¯®áâ®ïë© ¬ £¨âë© ¯®â®ª, ã¯à ¢«¥¨¥ ®áãé¥á⢫ï¥âáï ¨§¬¥¥¨¥¬ í«¥ªâத¢¨¦ã饩 á¨«ë ¨áâ®ç¨- ª ¢ 类ன 楯¨ e(t). ãâ२¬ ᮯà®â¨¢«¥¨¥¬ ¨áâ®ç-
¨ª ¯à¥¥¡à¥£ ¥¬. 室묨 ¢®§¤¥©á⢨ﬨ áç¨â ¥¬ e(t) ¨ ¯à¨¢¥¤¥ë© ¬®¬¥â £à㧪¨ ¢ «ã ¤¢¨£ ⥫ï M(t): ë- 室 ¬¨ á¨á⥬ë áç¨â ¥¬ 㣮« ¯®¢®à®â à®â®à (t) ¨ ⮪ ¢ 类ன ®¡¬®âª¥ i(t). ¨ ¬¨ªã á¨áâ¥¬ë ¬®¦® ®¯¨á âì á«¥- ¤ãî騬¨ ãà ¢¥¨ï¬¨ [15, 76]:
8 |
|
|
|
d (t) |
= !(t) |
|
|
|
|
di(t) |
|
dt |
|
|
|
|
|
L |
+ Ri(t) = e(t) |
|
Ce!(t) |
(1.14) |
||||
dt |
|
|||||||
> |
; |
|
||||||
|
|
|
d!(t) |
|
|
|
||
< |
|
|
|
= CM i(t) ; M(t): |
|
|||
> |
|
|
J |
dt |
|
|||
: |
|
|
|
|
26 |
|
|
|
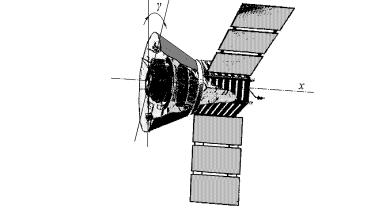
¤¥áì ®¡®§ ç¥ë: L, R { ¨¤ãªâ¨¢®áâì ¨ ªâ¨¢®¥ ᮯà®â¨- ¢«¥¨¥ 类ன 楯¨, J { ¯à¨¢¥¤¥ë© ¬®¬¥â ¨¥à樨 à®â®-
à, Ce CM { ¯®áâ®ïë¥, § ¢¨áï騥 ®â ª®áâàãªâ¨¢ëå ¯ -
ଥâ஢ ¤¢¨£ â¥«ï ¨ ¢¥«¨ç¨ë ¯®â®ª ¢®§¡ã¦¤¥¨ï.
¤ ®¬ ¯à¨¬¥à¥ n = 3 m = l = 2: ¢¥¤¥¬ ¢¥ªâ®à á®áâ®- ï¨ï â ª, çâ®¡ë ¥£® ª®¬¯®¥âë ᮮ⢥âá⢮¢ «¨ § 票ï¬
|
|
|
|
T |
|
3 |
: |
«®£¨ç® ®¯à¥- |
|
(t) i(t) !(t) : x(t) = [ (t) i(t) |
!(t)] |
|
|||||||
|
|
|
|
T2R |
|
|
2 |
¨ ¢¥ªâ®à ¢ë室 |
|
¤¥«¨¬ ¢¥ªâ®à ¢å®¤ u(t) = [e(t) |
M(t)] |
2 R |
|||||||
|
|
T |
|
|
|
|
|||
y(t) = [ (t) |
i(t)] |
|
2R2: ª «¥£ª® ã¡¥¤¨âìáï, ãà ¢¥¨ï (1.14) |
||||||
¯à¨¨¬ îâ ¢¨¤ (1.3), ¢ ª®â®àëå |
|
|
|
|
|
|
|||
|
2 |
|
; |
|
;1 |
; |
|
3 |
|
2 |
|
|
;1 3 |
|
|
|
0 |
0 |
0 |
|
|
1 |
5 |
|
4 |
0 |
0 |
5 |
|
|
41 |
0 |
|
|
|
|
|
|
|
|||||
A = |
|
0 RL;1 |
|
CeL;1 |
|
B = |
|
L;1 |
0 |
|
|
|||
|
|
0 |
CM J |
|
|
0 |
|
|
|
0 |
;J |
|
|
|
C = 0 |
1 |
0 : |
|
|
|
|
|
|
|
|
|
|||
1.4.2.¥â ⥫ìë¥ ¯¯ à âë
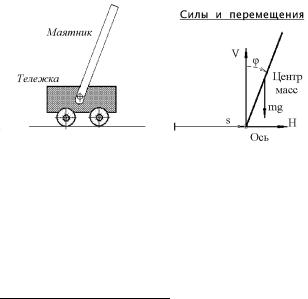
ਬ¥à 1. £«®¢®¥ ¤¢¨¦¥¨¥ ¨áªãáá⢥®£® á¯ãâ¨- ª ¥¬«¨. áᬮâਬ ã¯à®é¥ãî ¬®¤¥«ì 㣫®¢®£® ¤¢¨- ¦¥¨ï ¨áªãáá⢥®£® á¯ã⨪ ¥¬«¨ ( ) ®â®á¨â¥«ì®
¯à®¤®«ì®© ®á¨ [19], à¨á. 1.4.
¨á. 1.4. áªãááâ¢¥ë© á¯ã⨪ ¥¬«¨.
27

¡®§ 稬 ç¥à¥§ (t) !x(t) { 㣮« ¨ 㣫®¢ãî ᪮à®áâì ªà¥- \ Jx { ¬®¬¥â ¨¥à樨 ®â®á¨â¥«ì® ¯à®¤®«ì- ®© ®á¨ x\ Mx(t) { ã¯à ¢«ïî騩 ¬®¬¥â ®â®á¨â¥«ì® í⮩
®á¨, à §¢¨¢ ¥¬ë©, ¯à¨¬¥à, ॠªâ¨¢ë¬¨ ¤¢¨£ ⥫ﬨ. - ¯¨è¥¬ ãà ¢¥¨¥ ¤¨ ¬¨ª¨ ¢à é ⥫쮣® ¤¢¨¦¥¨ï ¨ ª¨¥- ¬ â¨ç¥áª®¥ á®®â®è¥¨¥, á¢ï§ë¢ î饥 㣮« ¨ 㣫®¢ãî ᪮- à®áâì. ®«ã稬
|
d (t) |
= |
!x (t) |
(1.15) |
|
dt |
|
Mx(t) |
|
8 d!x(t) |
|
|
||
< |
dt |
= |
Jx |
: |
«ï ¤ ®© á¨á⥬ë: |
n = 2 |
m = 1: áâ¥áâ¢¥ë¬ ®¡à §®¬ |
||
¬®¦® ®¯à¥¤¥«¨âì ¢¥ªâ®à á®áâ®ï¨ï, ᮯ®áâ ¢¨¢ ¥£® ª®¬¯®-
|
|
|
T |
¥â ¬ § 票ï 㣫 ¨ 㣫®¢®© ᪮à®áâ¨: x(t) = [ (t) !x(t)] : |
|||
®¢ ¯®«ãç ¥¬ ãà ¢¥¨ï ¢¨¤ |
(1.3), ¢ ª®â®àëå ¬ âà¨æë |
|
|
0 |
1 |
0 |
|
A = 0 |
0 B = Jx;1 : |
|
|
¨¤ ¬ âà¨æë C ®¯а¥¤¥«п¥вбп в¥¬, ª ª¨¥ ¯¥а¥¬¥л¥ ¨§¬¥- аповбп ¨«¨ ®в®б¨в¥«м® ª ª¨е ¨§ ¨е д®а¬г«¨аг¥вбп ж¥«м г¯а ¢«¥¨п. ¯а¨¬¥а, ¥б«¨ ¨§¬¥ап¥вбп в®«мª® г£®« ªа¥ ,
â® l = 1 ¨ C = [1 |
0]: б«¨ ¨§¬¥аповбп ®¡¥ ¯¥а¥¬¥л¥, в® |
|||||||
l = 2 |
C = I2 : |
8 |
|
|
|
|
||
ਬ¥à 2. |
த®«ì®¥ ¤¢¨¦¥¨¥ «¥â ⥫쮣® |
¯¯- |
||||||
à â |
¢ |
⬮áä¥à¥. |
ª ¨§¢¥áâ®, ãà ¢¥¨ï ¯à®¤®«ì®£® |
|||||
¤¢¨¦¥¨ï «¥â ⥫쮣® |
¯¯ à â ( ) ¢ ⬮áä¥à¥ (à¨á. 1.5) |
|||||||
¬®£ãâ ¡ëâì § ¯¨á ë ¢ ¢¨¤¥ [19, 23, 98] |
|
|||||||
|
mV_ (t)=;mg sin + P cos ; qS (cx cos + cy sin ) |
|
||||||
8 mV _(t)=;mg cos + P sin + qS (;cx sin + cy cos ) |
|
|||||||
> |
Jz!z |
=qSbmz |
|
(1.16) |
||||
|
#_(t)=!z |
|
|
|||||
|
|
|
|
|
|
|||
< x(t)=V cos cos |
|
|
|
|
||||
|
_ |
|
|
|
|
|
|
|
> H (t)=V sin |
|
|
|
|
||||
£¤:¥ #, , |
{ 㣫ë â £ ¦ , ª«® ¨ ¯®¢®à®â âà ¥ªâ®à¨¨\ |
|||||||
= # |
; |
{ 㣮« |
â ª¨\ V { §¥¬ ï ᪮à®áâì \ mg { á¨- |
|||||
« |
â殮áâ¨\ S b { å à ªâ¥à ï ¯«®é ¤ì ¨ «¨¥©ë© à §¬¥à |
|||||||
|
|
|
|
|||||
8 |
¤¥áì ¨ ¤ «¥¥ ç¥à¥§ In ®¡®§ ç¥ ¥¤¨¨ç ï ¬ âà¨æ ¯®à浪 |
n: |
||||||
®£¤ |
¨¤¥ªá n |
¢ § ¯¨á¨ ¡ã¤¥â ®¯ã᪠âìáï. |
|
|||||
|
|
|
|
|
|
28 |
|
|

¨á. 1.5. ¬®«¥â ¨ ¥£® ¯à®¤®«ìë¥ ã£«®¢ë¥ ª®®à¤¨ âë.
\ Jz { ¬®¬¥â ¨¥à樨 ®â®á¨â¥«ì® ¡®ª®¢®© ®á¨\ q { ᪮à®á⮩ ¯®à\ x H { §¥¬ë¥ ª®®à¤¨ âë æ¥âà ¬ áá\ P { ᨫ â ¤¢¨£ ⥫ï\ cx cy mz { ª®íää¨æ¨¥âë «®-
¡®¢®£® ᮯà®â¨¢«¥¨ï, ¯®¤ê¥¬®© á¨«ë ¨ ¬®¬¥â â £ ¦ . 票ï íâ¨å ª®íää¨æ¨¥â®¢ á«®¦ë¬ ®¡à §®¬ § ¢¨áïâ ®â ᪮à®á⨠, 㣫®¢ â ª¨ ¨ ®âª«®¥¨ï àã«¥¢ëå ®à£ ®¢,
⪦¥ ®â ¢ëá®âë ¨ ᪮à®á⨠¯®«¥â .
१ã«ìâ ⥠«¨¥ ਧ 樨, ãà ¢¥¨ï (1.16) ¢ ®âª«®¥¨- ïå ®â § ¤ ®© "®¯®à®©" âà ¥ªâ®à¨¨ ¯à¨¢®¤ïâáï ª ãà ¢¥-
¨ï¬ á®áâ®ï¨ï (1.3) á ¬ âà¨æ ¬¨ [23]
|
2 |
|
aV |
|
|
a |
+ a |
0 |
a |
0 |
aH |
3 |
|
|
|
|
x |
|
|
x |
|
x |
|
x |
|
x |
|
||
|
|
;aV |
|
|
;a |
+ a |
0 |
;a |
0 |
;aH |
|
|||
|
|
; Vy |
|
|
; y |
|
y |
!z |
; y |
0 |
; Hy |
|
||
A = |
|
|
;amz |
|
|
amz |
|
;amz |
;amz |
;amz |
|
|
||
|
6 |
|
0 |
|
|
|
0 |
|
1 |
0 |
0 |
0 |
7 |
|
|
cos cos |
|
; |
V sin cos |
0 |
0 |
0 |
0 |
|
|||||
|
|
sin |
|
V cos |
0 |
0 |
0 |
0 |
|
|||||
|
4 a ¤ |
a ¢ |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
2 |
x |
x |
3 |
|
|
|
|
|
|
|
|
|
|
|
a ¤ |
;a ¢ |
|
|
|
|
|
|
|
|
|
|
||
|
y¤ |
y ¢ |
|
|
|
|
|
|
|
|
|
|
||
B = |
6 |
amz |
;amz |
7 |
|
|
|
|
|
|
|
(1.17) |
||
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
||
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
00
£¤¥ |
4 |
5 |
|
: ª ç¥á⢥ ¢¥ªâ®- |
|
{ ®¯®àë¥ § 票ï 㣫®¢ |
|||
à |
á®áâ®ï¨ï ¢§ïâ ¢¥ªâ®à ®âª«®¥¨© ª®®à¤¨ â ¤¢¨¦¥¨ï |
|||
á¨áâ¥¬ë ®â ®¯®àëå: |
|
T |
||
x = [ V !z # x H] : ¥ªâ®à |
||||
|
|
|
T |
{ ᨣ «ë ã¯à ¢«¥¨ï |
ã¯à ¢«¥¨ï u = [ ¤ ¢ ] £¤¥ ¤ ¢ |
||||
|
|
|
29 |
|
¤¢¨£ ⥫¥¬ ¨ àã«¥¬ ¢ëá®âë. 9
¨¤ ¬ âà¨æ C ¨ D § ¢¨б¨в ®в в®£®, ª ª¨¥ ¯¥а¥¬¥л¥ ¨§¬¥- аповбп ¤ вз¨ª ¬¨ ¨«¨ ¨б¯®«м§говбп ¯а¨ § ¯¨б¨ ж¥«¨ г¯а -
¢«¥¨ï.
1.4.3.¥å ¨ç¥áª¨¥ ª®áâàãªæ¨¨
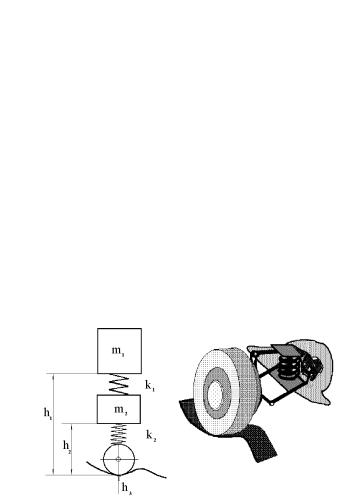
ਬ¥à 1. ¢¨¦¥¨¥ ¯¥à¥¢¥àã⮣® ¬ ï⨪ â¥-
«¥¦ª¥. áᬮâਬ ¯¥à¥¢¥àãâë© ("®¡à é¥ë©") ¬ ï⨪ (à¨á. 1.6), ®áì ª®â®à®£® ᬮâ¨à®¢ ⥫¥¦ª¥, ª®â®à ï ¬®¦¥â ¯¥à¥¬¥é âìáï ¢ £®à¨§®â «ì®¬ ¯à ¢«¥¨¨. â¥- «¥¦ªã ¢¤®«ì ¯à ¢«¥¨ï ¯¥à¥¬¥é¥¨ï ¤¥©áâ¢ã¥â ¢¥èïï ᨫ F (t): ¡®§ 稬: m ¨ M { ¬ ááë ¬ ï⨪ ¨ ⥫¥¦ª¨\ L { à ááâ®ï¨¥ ¬¥¦¤ã ®áìî ¢à é¥¨ï ¬ ï⨪ ¨ ¥£® æ¥- â஬ â殮áâ¨\ J { ¬®¬¥â ¨¥à樨 ¬ ï⨪ ®â®á¨â¥«ì® ®á¨ ¢à 饨ï\ k { ª®íää¨æ¨¥â "¢ï§ª®£®" â२ï\ g { ã᪮- २¥ ᢮¡®¤®£® ¯ ¤¥¨ï. ã«¥¢ãî â®çªã ®âáç¥â 㣫 ®âª«®¥¨ï ¬ ï⨪ '(t) ¯à¨¬¥¬ ¯à ¢«¥¨¥ "¢¥à⨪ «ì®
¢¢¥àå". ¥à¥§ s(t) ®¡®§ 稬 ¯¥à¥¬¥é¥¨¥ ⥫¥¦ª¨ ®â®á¨- â¥«ì® ¢ë¡à ®£® ç «ì®£® (ã«¥¢®£®) ¯®«®¦¥¨ï.
¨á. 1.6. ¥à¥¢¥àãâë© ¬ ï⨪.
á室 ï ¬ ⥬ â¨ç¥áª ï ¬®¤¥«ì á¨á⥬ë áâநâáï ®¤- ¨¬ ¨§ ¬¥â®¤®¢ ⥮à¥â¨ç¥áª®© ¬¥å ¨ª¨, á¬. [62], ¯à¨- ¬¥à, ¢ ¢¨¤¥ ãà ¢¥¨© £à ¦ ¢â®à®£® த . ª ¯®- ª § ®, ¯à¨¬¥à, ¢ [47], ã¯à®é¥ ï «¨¥ ਧ®¢ ï ¬®-
¤¥«ì ¤ ®© á¨áâ¥¬ë ®â®á¨â¥«ì® ¢¥ªâ®à á®áâ®ï¨ï x(t) =
9 «ï ªà ⪮á⨠§ ¯¨á¨ «¨¥ ਧ®¢ ëå ãà ¢¥¨© ᨬ¢®« ®¡ëç- ® ®¯ã᪠¥âáï.
30
[s s s+L0' s+L0']T ¨ ¢å®¤ |
u(t) = F (t) ¬®¦¥â ¡ëâì § ¯¨á |
||||||||||
¢ ¢¨¤¥ ãà ¢¥¨© (1.3) á ¬ âà¨æ ¬¨ |
|
|
|
|
|
||||||
6 ; |
0 |
|
1 |
0 |
0 |
7 |
6 |
0 |
7 |
|
|
A = 2 |
0 |
|
;kM;1 |
0 |
03 |
B = 2 M;1 |
3 |
(1.18) |
|||
4 |
0 |
|
0 |
0 |
1 |
5 |
4 |
0 |
5 |
|
|
|
gL1;1 |
0 |
gL1;1 |
0 |
|
|
0 |
|
|
||
£¤¥ ç¥à¥§ L1 |
= J |
2 |
|
|
íä䥪⨢ ï ¤«¨ |
¬ ïâ- |
|||||
+ mL ®¡®§ ç¥ |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
¨ª . |
|
|
mL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ª ¨ ¢ëè¥, ¢¨¤ ¬ âà¨æ C D ®¯à¥¤¥«ï¥âáï ãá«®¢¨ï¬¨ ¨§- |
|||||||||||
¬¥à¥¨ï. |
|
|
|
|
|
|
|
|
|
|
|
ਬ¥à 2. ¢¨¦¥¨¥ âà ᯮà⮣® á।á⢠|
¯® ¥- |
||||||||||
஢®© ¯®¢¥àå®áâ¨. áᬮâਬ ¤¢¨¦¥¨¥ ¤¢ãå¬ áᮢ®© |
|||||||||||
á¨á⥬ë, á®áâ®ï饩 ¨§ á¢ï§ ëå à¥áá®à ¬¨ ª®à¯ãá |
¬ áᮩ |
||||||||||
m1 ¨ ª®«¥á |
¬ áᮩ m2 ¯¥à¥¬¥é î饩áï ¯® ¥à®¢®© ¯®- |
||||||||||
¢¥àå®á⨠[126] (à¨á. 1.7). |
ç¨â |
¥¬, çâ® á¨á⥬ à ¡®â ¥â |
|||||||||
¨á. 1.7. à ᯮàâ ï á¨á⥬ .
¢ ®¡« á⨠«¨¥©ëå ã¯àã£¨å ¤¥ä®à¬ 権 ¨ ª®íää¨æ¨¥âë
¦¥á⪮á⨠à¥áá®àë ¨ ª®«¥á à ¢ë k1 k2: ¡®§ 稢 ç¥à¥§ |
|||||
h1(t) h2(t) h3 |
(t) ᮮ⢥âá⢥® ¢¥à⨪ «ì®¥ ¯¥à¥¬¥é¥¨¥ |
||||
ª®à¯ãá , ª®«¥á |
¨ ¢ëá®âã ¯®¢¥àå®á⨠(®â®á¨â¥«ì® ¥ª®â®- |
||||
ண® ã஢ï), ¤«ï ¢¥ªâ®à |
|
_ |
_ |
T |
|
x(t) = [h1 (t) |
h1(t) h2(t) |
h2 |
(t)] ¨ |
||
¢å®¤®£® ¢®§¤¥©á⢨ï u(t) = h3(t) ¯®«ã稬 ãà ¢¥¨ï á®áâ®ï- 31
