
Андриевский Б.Р., Фрадков А.Л. Избранные главы теории автоматического управления
.pdf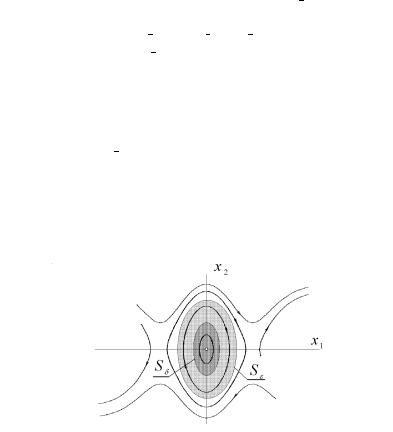
¥®¤®à®¤®£® (¢ ®¡é¥¬ á«ãç ¥) ãà ¢¥¨ï x(t) = f;x(t) t x(0) = x0 ¯®á«¥ § ¬¥ë ¯¥à¥¬¥ëå ¨ ¯®¤áâ ®¢ª¨ x0 = x0; x x(t) = x(t) + x x(t) = x(t) + x (t) ¯à¨å®¤¨¬ ª ãà ¢¥-
¨î ¢ ®âª«®¥¨ïå x(t) = f~; x(t) t ¢ ª®â®à®¬ äãªæ¨ï
f~(0 t) = 0 ¤«ï ¢á¥å t:
«¥¤®¢ ⥫ì®, à áᬮâà¥ë¥ § ¤ ç¨ á¢®¤ïâáï ª ¨áá«¥¤®- ¢ ¨î ¥¢®§¬ã饮£® ¤¢¨¦¥¨ï ãà ¢¥¨ï (11.14) «¨¡® ¡®- «¥¥ ®¡é¥£® ¥®¤®à®¤®£® ãà ¢¥¨ï
x(t) = f x(t) t f (0 t) = 0: |
|
ਢ¥¤¥¬ ¥ª®â®àë¥ ®¯à; |
¥¤¥«¥¨ï [12, 66, 76, 94]. |
¯à¥¤¥«¥¨¥ 1. ®«®¦¥¨¥ à ¢®¢¥á¨ï ãá⮩稢® (¯® ï- |
|
¯ã®¢ã) ¯à¨ t ! 1 ¥á«¨ ¤«ï «î¡®£® " > 0 ¬®¦® 㪠§ âì |
|
â ª®¥ > 0, çâ® ¤«ï ¢á¥å jjx0jj < á¯à ¢¥¤«¨¢® ¥à ¢¥á⢮ |
|
jjx(t)jj < " ¤«ï ¢á¥å t > 0: |
2 |
¨á. 11.5. á⮩稢®áâì ¯® ï¯ã®¢ã.
᫨ ç¥à¥§ S ®¡®§ ç¨âì ®¡« áâì jjxjj < â® ¤ ®¥ ®¯à¥- |
||||||||
¤¥«¥¨¥ ®§ ç ¥â, çâ® |
«î¡ ï âà ¥ªâ®à¨ï, ç¨ îé ïáï ¢ |
|||||||
S , ¥ ¤®á⨣¥â S": |
|
|
. ¯à¨¢¥¤¥®¬ ®¯à¥¤¥«¥¨¨ S S" { |
|||||
|
¬ ¥ ç |
|
¨ ¥ |
1 |
||||
áä¥à¨ç¥áª¨¥ ®¡« á⨠(¢ § ¤ ®© ®à¬®© jj jj ¬¥âਪ¥). å |
||||||||
¬®¦® áç¨â âì ¯à®¨§¢®«ì묨 § ¬ªãâ묨 ®£à ¨ç¥ë¬¨ |
||||||||
®¡« áâﬨ |
S |
|
S |
" |
S |
= 0 (à¨á. 11.5). |
||
|
|
|
|
6 f g |
||||
¬ ¥ ç |
|
¨ ¥ |
2 . ªâ¨ç¥áª¨ â ª®© ¢¨¤ ãá⮩稢®á⨠|
|||||
®§ ç ¥â ¥¯à¥àë¢ãî § ¢¨á¨¬®áâì à¥è¥¨© ®â ç «ìëå ãá«®¢¨©, à ¢®¬¥àãî ¯® t [12, 79].
|
¬ ¥ ç ¨ ¥ 3 . à® ãá⮩稢®áâì ¯® ï¯ã®¢ã |
¨®£¤ |
£®¢®àïâ, çâ® íâ® "ãá⮩稢®áâì ¢ ¬ «®¬". ¡« áâì |
|
262 |
S ®¡¥á¯¥ç¨¢ îé ï § ¤ ë¥ ®£à ¨ç¥ë¥ ®âª«®¥¨ï ®â á®áâ®ï¨ï à ¢®¢¥á¨ï, ¬®¦¥â ¨¬¥âì ¬ «ë¥ à §¬¥àë. ¦®, çâ® ® ¥ã«¥¢ ï. ª ç¥á⢥ ¯à¨¬¥à , ¬®¦® à áᬮâà¥âì "®¡à é¥ë© ¬ ï⨪" á áã娬 â२¥¬. ¬¥¥âáï ª®¥ç ï (¯ãáâì ¥¡®«ìè ï) ®¡« áâì ç «ìëå á®áâ®ï¨©, ¢ ª®â®à®¬ ¥£® ¢¥à⨪ «ì®¥ ¯®«®¦¥¨¥ ãá⮩稢®.
¬ ¥ ç ¨ ¥ 4 . ®«®¦¥¨¥ à ¢®¢¥á¨ï ãá⮩稢ëå «¨¥©ëå á¨á⥬ ãá⮩稢® ¯® ï¯ã®¢ã. ®«®¦¥¨¥ à ¢- ®¢¥á¨ï ¨ ¯à¥¤¥«ìë© æ¨ª« ¢â®ª®«¥¡ ⥫ìëå ¥«¨¥©ëå á¨á⥬, ¢®®¡é¥ £®¢®àï, ¥ãáâ®©ç¨¢ë ¯® ï¯ã®¢ã.
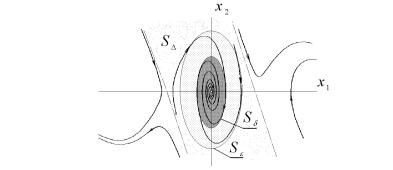
¨á. 11.6. ᨬ¯â®â¨ç¥áª ï ãá⮩稢®áâì ¯® ï¯ã®¢ã.
¯à¥¤¥«¥¨¥ 2. ®«®¦¥¨¥ à ¢®¢¥á¨ï ᨬ¯â®â¨ç¥áª¨ ãá⮩稢®, ¥á«¨: 1) ®® ãá⮩稢® ¯® ï¯ã®¢ã\ 2) áãé¥-
áâ¢ã¥â > 0 â ª®¥, çâ® ¤«ï «î¡®£® jjx0jj < ¢ë¯®«¥® |
|||
limt!1 x(t) = 0 (à¨á. 11.6). |
|
||
¡« áâì |
S §ë¢ ¥âáï ®¡« áâìî ¯à¨â殮¨ï, ¨«¨ ®¡« - |
||
áâìî ᨬ¯â®â¨ç¥áª®© ãá⮩稢®áâ¨, â®çª x0 = 0 { ¯à¨- |
|||
â¢ î饩 (¢ S ): |
2 |
|
|
¯à¥¤¥«¥¨¥ 3. ®«®¦¥¨¥ à ¢®¢¥á¨ï ᨬ¯â®â¨ç¥áª¨ |
|||
ãá⮩稢® |
¢ 楫®¬ |
(£«®¡ «ì® |
ᨬ¯â®â¨ç¥áª¨ ãá⮩稢®), |
¥á«¨ ¢ ãá«®¢¨ïå ¯à¥¤¥«¥¨ï 2, |
S = X { ¢á¥ ¯à®áâà á⢮ |
||
á®áâ®ï¨©. |
2 |
|
|
¯à¥¤¥«¥¨¥ 4. |
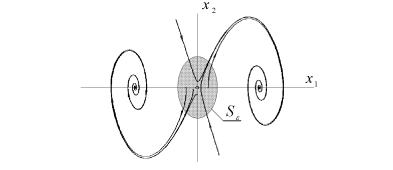
®«®¦¥¨¥ à ¢®¢¥á¨ï ¥ãá⮩稢® (¯® |
||
ï¯ã®¢ã), ¥á«¨ ¤«ï ¢á¥å > 0 ©¤¥âáï x0 2 S ) â ª®¥, ç⮠ᮮ⢥âáâ¢ãî饥 à¥è¥¨¥ § ª®¥ç®¥ ¢à¥¬ï ¤®á⨣¥â £à -
¨æ ®¡« á⨠S" (à¨á. 11.7). |
2 |
|
¬¥â¨¬, ç⮠ᨬ¯â®â¨ç¥áª¨ ãáâ®©ç¨¢ë¥ «¨¥©ë¥ á¨áâ¥- 263
¬ë £«®¡ «ì® ᨬ¯â®â¨ç¥áª¨ ãá⮩稢ë. ª¦¥ ®â¬¥â¨¬, çâ®, å®âï ã «¨¥©®© á¨á⥬ë, ä §®¢ë© ¯®àâà¥â ª®â®à®© ¨¬¥- ¥â ¢¨¤ 㧫 , ¨¬¥îâáï ᨬ¯â®â¨ç¥áª¨ áâ६ï騥áï ª á®áâ®- ï¨î à ¢®¢¥á¨ï âà ¥ªâ®à¨¨, â ª ï á¨á⥬ ¥ãá⮩稢 ¯®ï¯ã®¢ã.
¨á. 11.7. ¥ãá⮩稢®áâì ¯® ï¯ã®¢ã.
11.4.2. á⮩稢®áâì ¬®¦¥á⢠¨ ç áâ¨ç ï ãá⮩稢®áâì
«ï à áè¨à¥¨ï ª« áá à áᬠâਢ ¥¬ëå § ¤ ç ¨á¯®«ì§ã- îâáï ¨ ¤à㣨¥ ®¯à¥¤¥«¥¨ï ãá⮩稢®áâ¨. ®£¨¥ ¨§ ¨å á¢ï§ ë á ¯¥à¥å®¤®¬ ®â ãá⮩稢®á⨠â®çª¨ ¨«¨ ª®ªà¥â®© âà ¥ªâ®à¨¨ ª ãá⮩稢®á⨠¬®¦¥áâ¢.
¯à¨¬¥à, ¤«ï ¨áá«¥¤®¢ ¨ï ¢â®ª®«¥¡ ⥫ìëå á¨á⥬ ¨ ¤¢¨¦ãé¨åáï ¯® § ¬ªãâë¬ âà ¥ªâ®à¨ï¬ ®¡ê¥ªâ®¢, ¢¢®¤¨âáï
¯®ï⨥ ®à¡¨â «ì®© |
ãá⮩稢®áâ¨. «ï ¥£® ¨á¯®«ì§ã¥âáï |
|||||||
à ááâ®ï¨¥ (x |
G |
) |
|
|
|
|
G |
®¯à¥- |
|
¬¥¦¤ã â®çª®© x ¨ ¬®¦¥á⢮¬ |
|
||||||
¤¥«ï¥¬®¥, ª ª (x |
|
G) = infxz2G jjx ; xzjj: |
|
|
||||
¯à¥¤¥«¥¨¥ 5. |
à ¥ªâ®à¨ï |
G ®à¡¨â «ì® ãá⮩稢 , |
||||||
¥á«¨ ¤«ï «î¡®£® " > 0 ¬®¦® 㪠§ âì â ª®¥ > 0, çâ® ¤«ï |
||||||||
¢á¥å x0 â ª¨å, çâ® |
(x0 G) < |
á¯à ¢¥¤«¨¢® ¥à ¢¥á⢮ |
||||||
(x(t) G) < " ¤«ï ¢á¥å t > 0: |
2 |
|
|
|
||||
«®£¨ç®, ¬®¦® ¤ âì ¨ ®¯à¥¤¥«¥¨ï ᨬ¯â®â¨ç¥áª®© ®à¡¨â «ì®© ãá⮩稢®áâ¨, £«®¡ «ì®© ᨬ¯â®â¨ç¥áª®© ®à- ¡¨â «ì®© ãá⮩稢®á⨠¨ â.¤. ¤ ®¬ ®¯à¥¤¥«¥¨¨ à á- ᬠâਢ ¥âáï ¡«¨§®áâì à¥è¥¨ï ª ¯à®æ¥ááã, ª ª ª ¥ª®â®à®-
¬ã ¬®¦¥áâ¢ã â®ç¥ª. ®í⮬ã à ááâ®ï¨ï ¬¥¦¤ã â®çª ¬¨ ¢®§¬ã饮£® ¨ ¥¢®§¬ã饮£® ¤¢¨¦¥¨© ¢ ª ¦¤ë© ¤ ë©
264
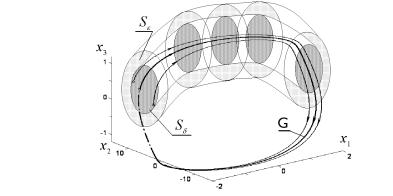
¬®¬¥â ¢à¥¬¥¨ ¬®£ãâ ®ª § âìáï ¡®«ì訬¨, ® âà ¥ªâ®à¨¨ ®áâ îâáï ¡«¨§ª¨¬¨ (à¨á. 11.8).
¨á. 11.8. ࡨ⠫ì ï ᨬ¯â®â¨ç¥áª ï ãá⮩稢®áâì.
㤥¬ ¯à¥¤¯®« £ âì, çâ® à¥è¥¨ï ãà ¢¥¨ï (11.14) ®¯à¥-
¤¥«¥ë ¡¥áª®¥ç®¬ ¨â¥à¢ «¥ ¢à¥¬¥¨ 0 t < +1: à - |
|
¥ªâ®à¨¨, ¯à®¤®«¦¥ë¥ |
¢¥áì íâ®â ¨â¥à¢ «, §ë¢ îâáï |
楫묨 âà ¥ªâ®à¨ï¬¨. |
¬¥â¨¬, çâ® ¤¢¨¦¥¨¥ ¨§®¡à ¦ - |
î饩 â®çª¨, ç¨ î饥áï ¢ ¯®«®¦¥¨¨ à ¢®¢¥á¨ï, ¨«¨ § ¬ªã⮩ âà ¥ªâ®à¨¨, ¡ã¤¥â ®áâ ¢ âìáï â ¬ ¤«ï ¢á¥å ¬®¬¥- ⮢ ¢à¥¬¥¨. ®®â¢¥âáâ¢ãî騥 ¬®¦¥á⢠â®ç¥ª ®¡à §ãîâ
¨¢ ਠâë¥ ¬®¦¥á⢠¢ ¯à®áâà á⢥ á®áâ®ï¨© [34, 94].
¯à¥¤¥«¥¨¥ 6. ¢ ਠâë¬ ¬®¦¥á⢮¬ M §ë¢ - ¥âáï ¬®¦¥á⢮ fxg â®ç¥ª â ª¨å, çâ® ¨§ x(t0) 2 M ¤«ï ¥ª®â®- ண® t0 á«¥¤ã¥â, çâ® x(t) 2 M ¤«ï ¢á¥å ;1 < t < +1:
᫨ íâ® ¬®¦¥á⢮ ¢ª«îç ¥â ¢á¥ ¢®§¬®¦ë¥ § 票ï
x(t0) ¤«ï ª®â®àëå ¢ë¯®«¥® 㪠§ ®¥ ãá«®¢¨¥, â® ®® - |
|
§ë¢ ¥âáï ¨¡®«ì訬 ¨¢ ਠâë¬ ¬®¦¥á⢮¬. |
2 |
¬¥¥âáï á«¥¤ãî饥 ®¯à¥¤¥«¥¨¥ ãá⮩稢®á⨠¨¢ à¨- ⮣® ¬®¦¥á⢠, ®¡®¡é î饥 ¯®ïâ¨ï ®à¡¨â «ì®© ãá⮩-
稢®á⨠¨ ãá⮩稢®á⨠¯®«®¦¥¨ï à ¢®¢¥á¨ï [28, 86]. |
|||
¯à¥¤¥«¥¨¥ 7. ¢ ਠ⮥ ¬®¦¥á⢮ |
M ãá⮩稢® |
||
(®â®á¨â¥«ì® á¨á⥬ë (11.14)), ¥á«¨ ¤«ï ¢á¥å |
" > 0 ¬®¦® |
||
㪠§ âì â ª®¥ > 0, çâ® ¤«ï ¢á¥å x0 |
â ª¨å, çâ® (x0 M) < |
||
¢ë¯®«¥® (x M) < " ¤«ï ¢á¥å t > |
0: |
2 |
|
«®£¨ç® ¤ ¥âáï ¨ ®¯à¥¤¥«¥¨¥ |
ᨬ¯â®â¨ç¥áª®© ãá⮩- |
||
稢®á⨠¨¢ ਠ⮣® ¬®¦¥á⢠. |
|
|
|
265 |
|
|
|

á⮩稢®áâì ¬®¦¥á⢠®â®á¨âáï ª ª« ááã ᢮©á⢠ç - áâ¨ç®© ãá⮩稢®á⨠á¨á⥬. à㣨¬ ¯®¤®¡ë¬ ᢮©á⢮¬
ï¥âáï ãá⮩稢®áâì ¯® ®â®è¥¨î ª äãªæ¨¨. |
áᬮ- |
||
âਬ á¨á⥬ã á ¢ë室®¬ |
|
|
|
x |
= |
f(x) |
(11.15) |
|
= |
h(x) |
(11.16) |
£¤¥ x 2 Rn, 2 Rnu , nu n, f(x) ¨ h(x) { ¥¯à¥àë¢ë¥ ¢¥ªâ®à- äãªæ¨¨. ãáâì á¨á⥬ (11.15) ¨¬¥¥â à ¢®¢¥á¨¥ x = x (®¡- 騩 á«ãç © ᢮¤¨âáï ª í⮬㠧 ¬¥®© ª®®à¤¨ â ¨ à áᬮ-
â२¥¬ ãà ¢¥¨© ¢®§¬ã饮£® ¤¢¨¦¥¨ï).
¯à¥¤¥«¥¨¥ 8. ¥è¥¨¥ x = x á¨á⥬ë (11.15) §ë¢ - ¥âáï ãáâ®©ç¨¢ë¬ ¯® ®â®è¥¨î ª äãªæ¨¨ h(x), ¥á«¨ ¤«ï «î- ¡®£® " > 0 ©¤¥âáï (") > 0, â ª®¥, çâ® ¤«ï ¢á¥å ç «ìëå
§ 票© x0, 㤮¢«¥â¢®àïîé¨å ãá«®¢¨î jx0 ; x j |
< à¥è¥- |
¨¥ x(t) á ç «ìë¬ ãá«®¢¨¥¬ x(0) = x0 ®¯à¥¤¥«¥® ¯à¨ ¢á¥å |
|
t 0 ¨ ¢ë¯®«ï¥âáï ¥à ¢¥á⢮ |
|
jh(x(t)) ; h(x )j < " ¤«ï ¢á¥å t 0: |
(11.17) |
᫨ à¥è¥¨¥ x = x ãá⮩稢® ¯® ®â®è¥¨î ª h(x) ¨, ªà®¬¥ ⮣®, ¢ë¯®«ï¥âáï ãá«®¢¨¥ ââà ªâ¨¢®áâ¨
lim h(x(t)) = h(x ) |
(11.18) |
t!1 |
|
â® à¥è¥¨¥ x §ë¢ ¥âáï ᨬ¯â®â¨ç¥áª¨ ãáâ®©ç¨¢ë¬ ¯®
®â®è¥¨î ª äãªæ¨¨ h(x).
᫨ à¥è¥¨¥ x = x ãá⮩稢® ¯® ®â®è¥¨î ª äãªæ¨¨ h(x), ¢á¥ à¥è¥¨ï á¨á⥬ë (11.15) ®¯à¥¤¥«¥ë ¯à¨ ¢á¥å t 0 ¨ ãá«®¢¨¥ ââà ªâ¨¢®á⨠(11.18) ¢ë¯®«ï¥âáï ¤«ï «î¡ëå - ç «ìëå ãá«®¢¨© x0, â® à¥è¥¨¥ x = x (¨ á¨á⥬ (11.15))
§ë¢ ¥âáï £«®¡ «ì® ᨬ¯â®â¨ç¥áª¨ ãá⮩稢®© ¯® ®â®-
è¥¨î ª äãªæ¨¨ h(x).
祢¨¤®, ¯à¨ nu = n ¨ h(x) = x ®¯à¥¤¥«¥¨¥ 8 ᮢ¯ ¤ ¥â á® áâ ¤ àâ묨 ®¯à¥¤¥«¥¨ï¬¨ ãá⮩稢®á⨠¯® ï¯ã®¢ã ¨ ᨬ¯â®â¨ç¥áª®© ãá⮩稢®áâ¨. ¬ . . ï¯ã®¢ § - ¨¬ «áï ¨áá«¥¤®¢ ¨ï¬¨ ¨¬¥® í⮣® ç á⮣® á«ãç ï. 1957 £. . . ã¬ï楢 áä®à¬ã«¨à®¢ « ªà¨â¥à¨¨ ãá⮩ç¨- ¢®á⨠¯® ®â®è¥¨î ª ç á⨠¯¥à¥¬¥ëå, ᮮ⢥âáâ¢ãî饩 á«ãç î x = colfy zg h(x) = y. ®¤à®¡¥¥ ® ᢮©áâ¢ å ¨ ãá«®-
¢¨ïå ç áâ¨ç®© ãá⮩稢®á⨠á¬. ¢ [28, 29, 64, 86]. ⬥⨬, 266

çâ® ãá⮩稢®áâì ¯® ®â®è¥¨î ª äãªæ¨¨ h(x) ¥ ᢮¤¨âáï ª ãá⮩稢®á⨠¬®¦¥á⢠fx:h(x) = h(x )g, ª ª ¯®ª §ë¢ ¥â á«¥¤ãî騩 ¯à¨¬¥à.
ਬ¥à. áᬮâਬ á¨á⥬ã 2-£® ¯®à浪
x1 |
= x1 |
2x2 |
|
|
(11.19) |
x2 |
= ;1+x12 : |
|
|
||
à¨ ç «ìëå ãá«®¢¨ïå x1 (0) = 1, x2(0) = a á¨á⥬ |
¨¬¥¥â |
||||
à¥è¥¨¥ |
|
|
|
|
|
x1(t) = et x2(t) = a(1 + e;2t) |
: |
(11.20) |
|||
|
2 |
|
|
||
áᬮâਬ äãªæ¨î ¢ë室
x22
1 + x21
¨ ¢ëç¨á«¨¬ ᪮à®áâì ¥¥ ¨§¬¥¥¨ï ¢¤®«ì à¥è¥¨© á¨á⥬ë:
_ |
|
4x22 |
|
x22x12 |
|
|
x12 |
|
h(x1 |
x2) = ;1 + x12 |
+ |
(1 + x12)2 |
= ;4h(x1 x2) 1 |
; 4(1 + x12) : |
|||
«¥¤®¢ ⥫ì®, ;4h h_ ;3h 0 ¨, § ç¨â, h(x1 (t)x2(t)) ! 0 ¨ h_ (x1(t) x2(t)) ! 0 ¯à¨ t ! 1. ¤ ª®, ¨ª ª®¥ à¥è¥¨¥ (11.19) á ç «ìë¬ ãá«®¢¨¥¬ x2(0) = a 6= 0 ¥ áâ६¨âáï ª ¬®¦¥áâ¢ã S = f(x1 x2): h(x1 x2) = 0g = f(x1 x2): x2 = 0g. â® «¥£ª® ¢¨¤® ¨§ (11.20). 2
ਠ¨áá«¥¤®¢ ¨¨ á¨á⥬, ¯®¤¢¥à¦¥ëå ®£à ¨ç¥ë¬ ¢®§¬ã饨ï¬, ®ª §ë¢ îâáï ¯®«¥§ë¬¨ á«¥¤ãî騥 ¤¢ ®¯à¥- ¤¥«¥¨ï [34, 64].
¯à¥¤¥«¥¨¥ 9. ¨á⥬ §ë¢ ¥âáï ãá⮩稢®© ¯® - £à ¦ã, ¥á«¨ ª ¦¤®¥ ¥¥ à¥è¥¨¥ ¥®£à ¨ç¥® ¯à®¤®«¦ ¥¬®
¢¯à ¢®, â.¥. ¨¬¥¥â á¬ëá« ¯à¨ 0 |
t 1 ¨ ¢á¥ ä §®¢ë¥ âà ¥ª- |
|
â®à¨¨ ®£à ¨ç¥ë [0 1) (à¨á. 11.9). |
2 |
|
¯à¥¤¥«¥¨¥ 10. ¨á⥬ §ë¢ ¥âáï ¯à¥¤¥«ì® ®£à ¨ç¥- ®© (¤¨áᨯ ⨢®© ¯® ¥¢¨á®ã), ¥á«¨ áãé¥áâ¢ãîâ ®¡« áâ¨
S , S â ª¨¥, çâ® S S ¨ ¤«ï ¢á¥å x0 2 S áãé¥áâ¢ã¥â ¬®- |
|||||
¬¥â ¢à¥¬¥¨ t < |
1 |
(¢®§¬®¦®, § ¢¨áï騩 ®â x0), çâ® ¯à¨ |
|||
¢á¥å t t |
|
|
|
2 |
|
|
¢ë¯®«¥® x0 2 S . |
|
|||
¤ ®¬ ®¯à¥¤¥«¥¨¨ S §ë¢ îâ ¨®£¤ ®¡« áâìî ¤¨á- |
|||||
ᨯ 樨, |
|
S { ¯à¥¤¥«ìë¬ ¬®¦¥á⢮¬. |
|||
|
|
|
|
|
267 |
¨á. 11.9. á⮩稢®áâì ¯® £à ¦ã.
¨á. 11.10. ¨áᨯ ⨢®áâì ¢ 楫®¬.
᫨ S { ¢á¥ ¯à®áâà á⢮, â® á¨á⥬ §ë¢ ¥âáï
¤¥«ì® ®£à ¨ç¥®© ¢ 楫®¬ (à¨á. 11.10).
л¥ ®¯а¥¤¥«¥¨п п¢«повбп ¨¡®«¥¥ а б¯а®бва ¥- л¬¨, е®вп ¯а¥¤бв ¢«пов б®¡®© ¬ «го з бвм ®¯а¥¤¥«¥¨© гбв®©з¨¢®бв¨, ¨б¯®«м§г¥¬ле ¢ в¥®а¨¨ б¨бв¥¬.
11.4.3. ãªæ¨¨ ï¯ã®¢
¥à¥©¤¥¬ ⥯¥àì ¥¯®á।á⢥® ª ¨§«®¦¥¨î ®á®¢ëå ¨¤¥© ¨ ¥ª®â®àëå १ã«ìâ ⮢ ¬¥â®¤ äãªæ¨© ï¯ã®¢ .
祬 à áᬮâ२¥ á® á«¥¤ãî饣® ¯à¨¬¥à .
áᬮâਬ á¨á⥬㠯¥à¢®£® ¯®à浪 , n = 1 ãà ¢¥¨¥ 268

ª®â®à®© ¨¬¥¥â ¢¨¤
x(t) = f (x) f (0) = 0: |
(11.21) |
ãáâì äãªæ¨ï f(x) 㤮¢«¥â¢®àï¥â ¤®¯®«¨â¥«ì®¬ã ãá«®- ¢¨î xf (x) < 0 ¯à¨ x 6= 0 â.¥. ¥¥ £à 䨪 «¥¦¨â 楫¨ª®¬ ¢® ¢â®à®¬ ¨ ç¥â¢¥à⮬ ª¢ ¤à â å, ¯à¨ç¥¬ f (x) = 0 ⮫쪮 ¢
â®çª¥ x = 0: à㣮© ¨ä®à¬ 樨 ® ¢¨¤¥ í⮩ äãªæ¨¨ ¥â.ॡã¥âáï ¨áá«¥¤®¢ âì ãá⮩稢®áâì á®áâ®ï¨ï à ¢®¢¥á¨ï á¨á⥬ë (11.21).
12x2: ¬¥â¨¬, çâ® V (0) = 0 ¨ V (x) > 0 ¯à¨ x =6 0: 票ï x = x(t) ¬¥повбп ¢ б®®в¢¥вбв¢¨¨ б га ¢¥¨¥¬ (11.21). «¥¤®¢ в¥«м®, ¢ б¨«г
нв®£® га ¢¥¨п ¡г¤гв в ª¦¥ ¨§¬¥пвмбп ¨ § з¥¨п дгªж¨¨ |
||
; |
|
|
V (x) = V x(t) |
|
: ©¤¥¬ ¯à®¨§¢®¤ãî í⮩ äãªæ¨¨ ¯® ¢à¥- |
¬¥¨ ¢ ᨫã ãà ¢¥¨ï (11.21). ® ¯à ¢¨«ã ¤¨ää¥à¥æ¨à®- |
||
¢ ¨ï á«®¦®© äãªæ¨¨ ¯®«ãç ¥¬ V_ (x) = x(t)x(t) = xf(x), |
||
|
|
_ |
â.¥. ¤«ï ª ¦¤®£® ¬®¬¥â ¢à¥¬¥¨ § 票¥ V (x) ®¯à¥¤¥«ï- |
||
¥âáï ¢ ª ¦¤®© â®çª¥ ¯à®áâà á⢠á®áâ®ï¨© ¯® ª®®à¤¨ â ¬
í⮩ |
_â®çª¨ ¨ § 票î äãªæ¨¨ f (x): ®í⮬㠤«ï 宦¤¥- |
||||||
¨ï V (x) ¥ âॡã¥âáï ¯®«ãç âì à¥è¥¨ï (11.21)._ |
|
||||||
|
«¥¥ § ¬¥â¨¬, çâ® ¯à¨ ¢á¥å x = 0 ¢ë¯®«¥® V (x) < 0 § - |
||||||
|
|
|
|
6 |
|
|
|
ç¨â, äãªæ¨ï V (t) ¬®®â®® ã¡ë¢ ¥â, áâ६ïáì ¯à¨ t ! 1 ª |
|||||||
ã«î. «¥¤®¢ ⥫ì®, ¢¥«¨ç¨ |
jx(t)j |
â ª¦¥ ¡ã¤¥â ¬®®â®® |
|||||
ã¡ë¢ âì (çâ® á«¥¤ã¥â ¨§ ¢¨¤ |
äãªæ¨¨ V (x)) ¨ x(t) |
! 0 ¯à¨ |
|||||
t |
! 1 |
) ®í⮬㠬®¦® ᤥ« âì ¢ë¢®¤, çâ® á¨á⥬ |
(11.21) |
||||
|
|
|
13 |
«¥¤ã¥â ®¡à â¨âì |
|||
|
ᨬ¯â®â¨ç¥áª¨ ãá⮩稢 ¢ 楫®¬. |
|
|||||
¢¨¬ ¨¥ â®, çâ® ¢ë¢®¤ ®¡ ãá⮩稢®á⨠á®áâ®ï¨ï à ¢- ®¢¥á¨ï ¯®«ãç¥ ¡¥§ à¥è¥¨ï ãà ¢¥¨ï (11.21), ¡®«¥¥ ⮣®,
{¯à¨ á ¬ëå ®¡é¨å ¯à¥¤¯®«®¦¥¨ïå ® ¢¨¤¥ äãªæ¨¨ f (x).
ë© ¯à¨¬¥à ®â®á¨«áï ª á¨á⥬¥ ¯¥à¢®£® ¯®à浪 . §-
« £ ¥¬ë¥ ¨¦¥ â¥®à¥¬ë «ï¯ã®¢áª®£® ⨯ ¯à¨¬¥¨¬ë ¤«ï ¯à®¨§¢®«ì®£® n:
áᬮâà¥ ï ¢ ¤ ®¬ ¯à¨¬¥à¥ äãªæ¨ï ï¥âáï ¯à¥¤- áâ ¢¨â¥«¥¬ äãªæ¨© ï¯ã®¢ . ¬¥¥âáï ¥áª®«ìª® ®¯à¥¤¥«¥- ¨© íâ¨å äãªæ¨©. ®í⮬ã 㬥áâ® ®¡à â¨âìáï ª à §êïá¥- ¨î, ¤ ®¬ã á ¬¨¬ . . ï¯ã®¢ë¬ ¢ ¥£® ®á®¢®¯®« £ î-
饬 âà㤥 1892 £. [60].
13 ë §¤¥áì ®¯¨áë¢ ¥¬ á奬㠨ᯮ«ì§®¢ |
¨ï ¬¥â®¤ ï¯ã®¢ . ®ª § - |
⥫ìá⢠¯à¨¢¥¤¥ëå ¯®«®¦¥¨© ᮤ¥à¦ |
âáï, ¯à¨¬¥à, ¢ [12, 34, 79, 97]. |
269
" ¤à㣮¬ã [¬¥â®¤ã] ¬ë ¯à¨ç¨á«¨¬ ¢á¥ â¥, ª®â®àë¥ ®á®- ¢ë¢ îâáï ¯à¨æ¨¯ å, ¥ § ¢¨áïé¨å ®â à §ë᪠¨ï ª ª¨å- «¨¡® à¥è¥¨© ¤¨ää¥à¥æ¨ «ìëå ãà ¢¥¨© ¢®§¬ã饮£® ¤¢¨¦¥¨ï. ... \ ¨ ¢®®¡é¥ ¢ ®á®¢ ¨¨ ¢á¥å â¥å ¨§ ¨å, á ª®â®àë- ¬¨ ¢áâà¥â¨¬áï ¤ «¥¥, ¢á¥£¤ ¡ã¤¥â «¥¦ âì à §ë᪠¨¥ äãª- 権 ¯¥à¥¬¥ëå x1 x2 : : : xn t ¯® ¥ª®â®àë¬ ¤ ë¬ ãá«®¢¨- ï¬, ª®â®àë¬ ¤®«¦ë 㤮¢«¥â¢®àïâì ¨å ¯®«ë¥ ¯à®¨§¢®¤ë¥ ¯® t á®áâ ¢«¥ë¥ ¢ ¯à¥¤¯®«®¦¥¨¨, çâ® x1 x2 : : : xn áãâì äãªæ¨¨ t, 㤮¢«¥â¢®àïî騥 ãà ¢¥¨ï¬."
¬ . . ï¯ã®¢ ¯à¨¬¥ï« à §à ¡®â ë© ¨¬ ¬¥â®¤ ª
§¤ ç ¬ ¨áá«¥¤®¢ ¨ï ãá⮩稢®á⨠á¨á⥬. ¤ ª® ¢® ¢â®- ன ¯®«®¢¨¥ XX ¢. ¢ëïᨫ®áì, çâ® íâ®â ¯®¤å®¤ á ãᯥ宬 à ¡®â ¥â ¨ ¤«ï «¨§ ª ç¥á⢠á¨á⥬, ãá⮩稢®á⨠¬®- ¦¥áâ¢, ª®«¥¡ ⥫ì®á⨠¨ ¤àã£¨å ¤¨ ¬¨ç¥áª¨å ᢮©á⢠¥-
«¨¥©ëå á¨á⥬, â ª¦¥ ¤«ï à¥è¥¨ï § ¤ ç á¨â¥§ . â® ¯à¨¢¥«® ª ¯®¨¬ ¨î ¬¥â®¤ äãªæ¨© ï¯ã®¢ ª ª ¢¥¤ãé¥- £® ¬¥â®¤ ¨áá«¥¤®¢ ¨ï ¥«¨¥©ëå á¨á⥬.
¤ ®© £« ¢¥ ¬ë à áᬮâਬ «¨èì ®á®¢ë¥ â¥®à¥¬ë
¬¥â®¤ |
äãªæ¨© ï¯ã®¢ , â ª¦¥ ⨯¨çë¥ ¯à¨¬¥àë ¨å |
¯à¨¬¥¥¨ï ¤«ï «¨§ ãá⮩稢®á⨠á¨á⥬. |
|
11.4.4. |
á⮩稢®áâì ¥¯à¥àë¢ëå á¨á⥬ |
㤥¬ à áᬠâਢ âì äãªæ¨¨ V (x) 㤮¢«¥â¢®àïî騥 á«¥-
¤ãî騬 âॡ®¢ ¨ï¬: 1) V (x) ¥¯à¥àë¢ ¨ ¥¯à¥à뢮-¤¨ä- ä¥à¥æ¨à㥬 ¯® x ¢ ¥ª®â®à®© ®¡« á⨠X, ᮤ¥à¦ 饩 ç «® ª®®à¤¨ â\ 2) V (x) ®¡à é ¥âáï ¢ ®«ì ¢ ç «¥ ª®®à- ¤¨ â: V (0) = 0\ 3) V (x) ¯®«®¦¨â¥«ì® ®¯à¥¤¥«¥ , â.¥. ¯®- «®¦¨â¥«ì ¢áî¤ã, ªà®¬¥ ç « ª®®à¤¨ â: V (x) > 0 ¯à¨
x = 0: |
2 |
6 ãªæ¨ï W (x) §ë¢ ¥âáï ®âà¨æ â¥«ì® ®¯à¥¤¥«¥®©, ¥á«¨
;W (x) ¯®«®¦¨â¥«ì® ®¯à¥¤¥«¥ .
᫨ ¥®âà¨æ ⥫ì ï äãªæ¨ï ¬®¦¥â ®¡à é âìáï ¢ ®«ì ¥ ⮫쪮 ¯à¨ x = 0 â® ® §ë¢ ¥âáï ¥®âà¨æ â¥«ì® ®¯à¥-
¤¥«¥®© (§ ª®¯®«®¦¨â¥«ì®©).
«ï ä®à¬ã«¨à®¢ª¨ ¤ «ì¥©è¨å १ã«ìâ ⮢ ¯® ¤®¡¨âáï ¯à®¨§¢®¤ ï ¯® ¢à¥¬¥¨ äãªæ¨¨ ï¯ã®¢ ¢ ᨫã á¨c⥬ë (10.12) (ãà ¢¥¨ï ª®â®à®© ¯à¨ n = 1 ᮢ¯ ¤ îâ á (11.14)).
ᯮ«ì§ãï ¯à ¢¨«® ¤¨ää¥à¥æ¨à®¢ ¨ï á«®¦®© äãªæ¨¨ ¨ ®¯¥à æ¨î ¢ëç¨á«¥¨ï ¯à®¨§¢®¤®© ᪠«ïன äãªæ¨¨ ¯®
270

¢¥ªâ®à®¬ã à£ã¬¥âã ¯®«ã稬 14
V_ |
(x)=rxV (x)f (x)= |
@V |
|
@V |
(x)+ + |
@V |
@x1 f1 |
(x)+ |
@x2 f2 |
@xn fn(x):(11.22) |
ਢ¥¤¥¬ ⥯¥àì ä®à¬ã«¨à®¢ª¨ ¥ª®â®àëå ⥮६.¥®à¥¬ 1. ¡ ãá⮩稢®á⨠( . . ï¯ã®¢).
᫨ ¯à¨ x 2 áãé¥áâ¢ã¥â ¯®«®¦¨â¥«ì®-®¯à¥¤¥«¥ ï äãªæ¨ï V (x) â ª ï, çâ® ¥¥ ¯à®¨§¢®¤ ï ¢ ᨫã á¨á⥬ë (10.12) § ª®®âà¨æ ⥫ì , â® á®áâ®ï¨¥ à ¢®¢¥á¨ï ãá⮩ç¨- ¢® ¯® ï¯ã®¢ã.
¥®à¥¬ 2. ¡ ᨬ¯â®â¨ç¥áª®© ãá⮩稢®á⨠( . . ï- ¯ã®¢).
᫨ ¯à¨ x 2 áãé¥áâ¢ã¥â ¯®«®¦¨â¥«ì®-®¯à¥¤¥«¥ ï äãªæ¨ï V (x) â ª ï, çâ® ¥¥ ¯à®¨§¢®¤ ï ¢ ᨫã á¨á⥬ë (10.12) ®âà¨æ â¥«ì® ®¯à¥¤¥«¥ , â® á®áâ®ï¨¥ à ¢®¢¥á¨ï ᨬ¯â®â¨ç¥áª¨ ãá⮩稢® ¯® ï¯ã®¢ã.
¥®à¥¬ 3. ¡ ᨬ¯â®â¨ç¥áª®© ãá⮩稢®á⨠¢ ®¡« á⨠S ( ᨬ¯â®â¨ç¥áª®© ãá⮩稢®á⨠"¢ ¡®«ì讬") [93, 94].
᫨ ¯à¨ ¢ë¯®«¥¨¨ ãá«®¢¨© ⥮६ë 2 ¤«ï ¥ª®â®à®£®
C > 0 ¥à ¢¥á⢮ V (x) C ¢ë¯®«¥® ¢ § ¬ªã⮩ ®ªà¥áâ- ®áâ¨ ç « ª®®à¤¨ â S f0g 2 S â® á®áâ®ï¨¥ à ¢®¢¥- á¨ï f0g ᨬ¯â®â¨ç¥áª¨ ãá⮩稢® á ®¡« áâìî ¯à¨â殮¨ï S (á¬. ®¯à¥¤¥«¥¨¥ 2, á. 263).
¥®à¥¬ 4. ¡ ᨬ¯â®â¨ç¥áª®© ãá⮩稢®á⨠¢ 楫®¬
(⥮६ à¡ è¨ { à ᮢ᪮£®).
᫨ ¢ ãá«®¢¨ïå ¥®à¥¬ë 2 ¬®¦¥á⢮ ᮢ¯ ¤ ¥â á® ¢á¥¬ ¯à®áâà á⢮¬, â.¥. = X, V (x) ! 1 ¯à¨ kxk ! 1 â® á¨á- ⥬ ᨬ¯â®â¨ç¥áª¨ ãá⮩稢 ¢ 楫®¬.
ãªæ¨ï ï¯ã®¢ , 㤮¢«¥â¢®àïîé ï ¯à¨¢¥¤¥®¬ã ¢ ¤ - ®© ⥮६¥ ãá«®¢¨î à®áâ , ¨®£¤ §ë¢ ¥âáï à ¤¨ «ì® ¥-
®£à ¨ç¥®© [64, 93]. à® äãªæ¨î V (x t) § ¢¨бпйго п¢-
14 ®«¥§® ¨¬¥âì ¢ ¢¨¤ã á«¥¤ãî騥 ¯à ¢¨« ¤¨ää¥à¥æ¨à®¢ ¨ï [23]: ¯à®¨§¢®¤ ï ᪠«ïன äãªæ¨¨ V (x) ¯® ¢¥ªâ®àã x 2 Rn ï¥âáï 1 n-
¬ âà¨æ¥© ç áâëå |
¯à®¨§¢®¤ëå (â.¥. |
âà ᯮ¨à®¢ ®© ª ¢¥ªâ®àã- |
||||||
|
|
@V |
|
|
|
T |
|
|
á⮫¡æã £à ¤¨¥â |
V ¯® x): |
(rxV |
|
|
|
|||
@xi |
= |
(x)) |
= ¯à®¨§¢®¤ ï ¢¥ªâ®à- |
|||||
äãªæ¨¨ f(x) 2 Rm ¯® ¢¥ªâ®àã x 2 Rn ï¥âáï m n-¬ âà¨æ¥©, í«¥¬¥â - |
||||||||
¬¨ ª®в®а®© п¢«повбп з бвл¥ ¯а®¨§¢®¤л¥ |
@fj = ¯à®¨§¢®¤ ï ᪠«ïன |
|||||||
|
|
|
|
|
@xi |
|
||
äãªæ¨¨ V ¯® m n-¬ âà¨æ¥ A = faijg ï¥âáï m n-¬ âà¨æ¥©, í«¥¬¥- |
||||||||
в ¬¨ ª®в®а®© п¢«повбп з бвл¥ ¯а®¨§¢®¤л¥ |
@V |
= ¯à®¨§¢®¤ ï ª¢ ¤à - |
||||||
@aij |
||||||||
|
|
|
|
|
|
|
||
â¨ç®© ä®à¬ë xT Hx ¯® ¢¥ªâ®àã x2Rn à ¢ |
2xT H xT H + HxT : |
|||||||
|
|
|
271 |
|
|
|
||
