Методы вариационного исчисления и теории оптимального управления

Вариационное исчисление – математическая дисциплина, посвященная отысканию экстремальных (наибольших или наименьших) значений функционалов [1]. В свою очередь под функционалом понимается числовая (действительная или комплексная) функция, определенная на некотором множестве функций. Вариационное исчисление является естественным развитием той главы математического анализа, которая посвящена задаче отыскания экстремумов функций. В основе постановки задач классического вариационного исчисления лежат задачи управления физическими процессами. Во всех вариантах таких задач речь идет о способе задания наилучшего в том или другом смысле управления, обеспечивающего минимизацию или максимизацию некой цели управления.

В одной из возможных постановок [6] предметом вариационного исчисления является отыскание неизвестных функций или , реализующих максимум или минимум определенных интегралов вида

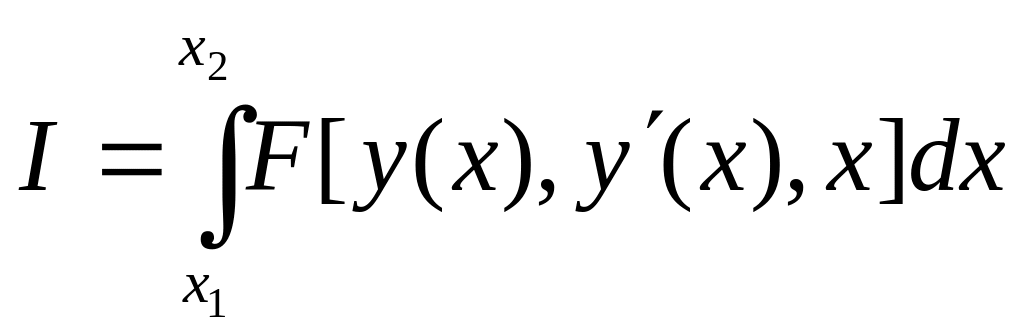
или

где ‑ функция, описывающая взаимосвязь поведения объекта в зависимости от управления. На функцию накладывается ряд требований, в частности, требования непрерывности производных на интервале определения, что всегда обеспечивается в задачах с физическими процессами и не всегда в задачах экономики и менеджмента. В большинстве приложений функции или выбираются не среди множества всех возможных функций от , а среди множества функций определенного класса. Такое допущение оправдано в связи с тем, что возможности управления процессом очень часто ограничивают класс возможных функций неким заранее заданным.

Развитие идей вариационного исчисления привело к определенной модернизации постановки исходной задачи в виде учета ограничений функции и созданию теории оптимального управления. Методы решения подобных задач опираются на реализацию так называемого принципа максимума Понтрягина [1]. Практическая реализация методов вариационного исчисления и теории оптимального управления позволяет решать динамические задачи разработки управленческого решения.

Метод сведения дискретной динамической задачи к статической

Одним из возможных методов разработки управленческого решения для динамических задач является метод, основанный на представлении динамической задачи в виде набора самостоятельно существующих статических задач. Пусть рассматривается дискретных моментов времени. Для каждого из них можно сформулировать самостоятельную задачу разработки управленческого решения (например, однокритериальную статическую в условиях определенности) ¹

где - текущий дискретный момент времени, .

Рассмотрим совместную однокритериальную статическую задачу в условиях определенности, решение которой представляет собой набор из самостоятельных решений для текущего момента времени . Будем считать, что критериальная функция новой совместной задачи определяется как сумма критериальных функций для каждого момента времени, а ограничения для каждого момента времени добавляются к общему списку ограничений задачи. Тогда условие новой задачи можно записать как

а общее количество уравнений ограничений увеличилось в раз. Таким образом, решение динамической задачи сводится к решению статической задачи разработки управленческого решения и может осуществляться рассмотренными ранее методами.

Реализация метода в общем случае приводит к существенному росту трудоемкости вычислений. Отметим, что если количество переменных при использовании метода всегда возрастает в раз, то число уравнений ограничений может быть значительно сокращено за счет конкретного рассмотрения динамических параметров. Так, если к категории динамических относятся один или несколько параметров , то рассмотрение каждого из них во времени увеличивает количество ограничений в раз. Для статических нет необходимости увеличивать количество уравнений, поскольку в этом случае они имеют смысл величины имеющегося ресурса на весь интервал планирования. Наконец, зависимость от времени неконтролируемых факторов и вообще может быть легко учтена при записи выражения целевой функции или ограничений особенно в численной форме.

Практическая реализация метода сведения динамических задач к статическим может быть осуществлена с использованием современных программных средств, реализующих, например, метод линейного программирования. При выборе используемой программы следует обращать внимание на ограничения программы по максимальному числу переменных и ограничений. Таким образом, метод сведения динамических задач к статическим может быть использован для решения динамических задач разработки управленческого решения.