Игры с противником.

Рассмотрим задачу разработки управленческого решения с одним неопределенным фактором , принимающим только два возможных значения при выборе противником соответственно стратегий и . Заметим, что хотя мы не знаем, какие конкретно значения на практике будут принимать неопределенные факторы, но мы можем предположить, что они примут определенные значения и вести дальнейшие рассуждения в отношении именно предполагаемых нами значений . Будем считать, что этот фактор влияет на критериальную функцию или на ограничения . Найдем два оптимальных решения и , с учетом двух возможных и предполагаемых нами стратегий противника и соответствующие выражениям

Полученные решения и представляют собой наши наилучшие действия (стратегии) и в том случае, когда мы угадали дальнейшее развитие событий. Используя уже полученные решения и , рассчитаем значения показателя эффективности при условии, что мы не угадали ответ противника:

Занесем полученные значения в так называемую платежную матрицу, где строки и представляют собой наши возможные стратегии, а столбцы и возможные стратегии противника

Стратегии

Очевидно, что аналогичная матрица может быть построена и при большем числе возможных стратегий , а также при большем числе неопределенных факторов .

Отыщем решение игры, пользуясь методами теории игр. Найдем нашу оптимальную стратегию, не зависящую от действий противника. В этом случае возникает вопрос о выборе критерия оптимальности. Например, в качестве используемой стратегии можно выбрать стратегию, которая приносит возможный максимальный выигрыш. Такая стратегия может оказаться весьма рискованной, поскольку в конкретной ситуации противник может ответить стратегией, приводящей к большему проигрышу. Более разумным представляется воспользоваться стратегией, которая минимизирует наш возможный проигрыш. Обозначим минимальный выигрыш при выборе стратегии при всех возможных стратегиях противника

.

Из всех возможных наших стратегий выберем стратегию, которая обеспечит нам наибольшее значение нашего минимального выигрыша

.

Назовем нижней ценой игры (наш гарантированный выигрыш при любой стратегии противника).

Если цели игроков противоположны, что имеет место в антагонистической игре, то противник заинтересован уменьшить наш выигрыш, и будет выбирать соответствующие стратегии. Вполне естественно предположить, что противник владеет методами оптимизации и теории игр и в свою очередь проводит аналогичные вычисления. Тогда полученная им платежная матрица будет иметь другие числовые значения, но ее смысл в отношении выбираемых стратегий не изменится. Поэтому мы можем анализировать возможные стратегии противника исходя из имеющейся у нас нашей платежной матрицы. Очевидно, что все это справедливо только в том случае, когда мы рассмотрели все возможные стратегии противника.

Примечание. Если противник не будет пользоваться оптимальными методами, то это просто приведет к его дополнительному проигрышу.

Найдем наш максимальный выигрыш при каждой стратегии противника

.

Для того чтобы минимизировать свой проигрыш, противник выберет стратегию, в которой наш выигрыш минимален

.

Назовем выигрыш верхней ценой игры. Очевидно, что если по каким-то причинам противник не воспользовался своей оптимальной стратегией, то наш выигрыш только возрастет. Если верхняя и нижняя цены игры совпадают, то их значение называют чистой ценой игры

.

Стратегии, соответствующие чистой цене игры, называются чистыми, а их совокупность дает оптимальное решение. Используя оптимальное решение, мы получаем минимальный гарантированный выигрыш независимо от поведения противника. Пара чистых стратегий и дает оптимальное решение игры тогда и только тогда, когда соответствующий им элемент является одновременно наибольшим в своем столбце и наименьшим в своей строке. Такая ситуация называется седловой точкой, а соответствующая ей игра - игрой с седловой точкой.

Если седловая точка в платежной матрице отсутствует, то существует несколько наших чистых стратегий и стратегий противника, позволяющих получить цену игры. Выбор нами одной из стратегий наталкивается на естественное противодействие противника, желающего минимизировать свой проигрыш и выбирающего ответную стратегию с учетом информации о нашем выборе. Это обстоятельство приводит к тому, что мы вынуждены хранить свой выбор в тайне и, кроме этого, чередовать свои стратегии при многократном повторении игры по случайному закону. Если так не делать, то противник привыкнет к тому, что мы играем одинаково, и с учетом этого будет строить свою игру. Смешанной стратегией называется применение стратегий , ,..., с вероятностями , ,…, , причем

. (8)

Будем записывать смешанные стратегии в виде матрицы

,

или в виде вектора . Смешанные стратегии противника запишем аналогично, обозначая соответствующие вероятности буквой :

,

,

или . Найдем оптимальную стратегию , обеспечивающую нам средний выигрыш не меньший, чем цена игры ( ). Математическое ожидание нашего выигрыша при реализации противником стратегии

.

Если - цена игры, то при условии имеем набор ограничений

.

Учитывая (8), будем искать набор , обеспечивающий максимальную цену игры , для чего сделаем замену переменных . Запишем итоговые выражения для целевой функции и ограничений задачи оптимизации выбора стратегий

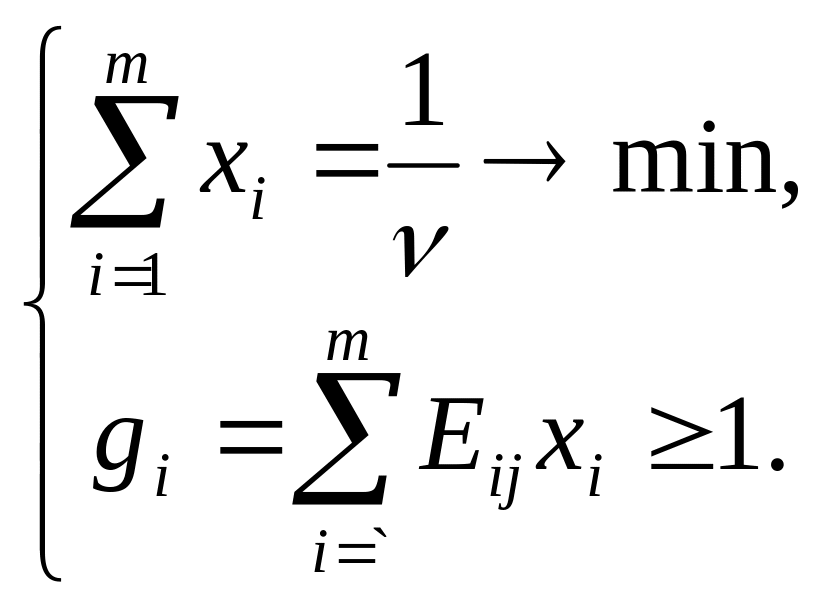
и решим задачу линейного программирования. Элементы нашей оптимальной смешанной стратегии определяются подстановкой . Оптимальная смешанная стратегия противника определяется аналогично:

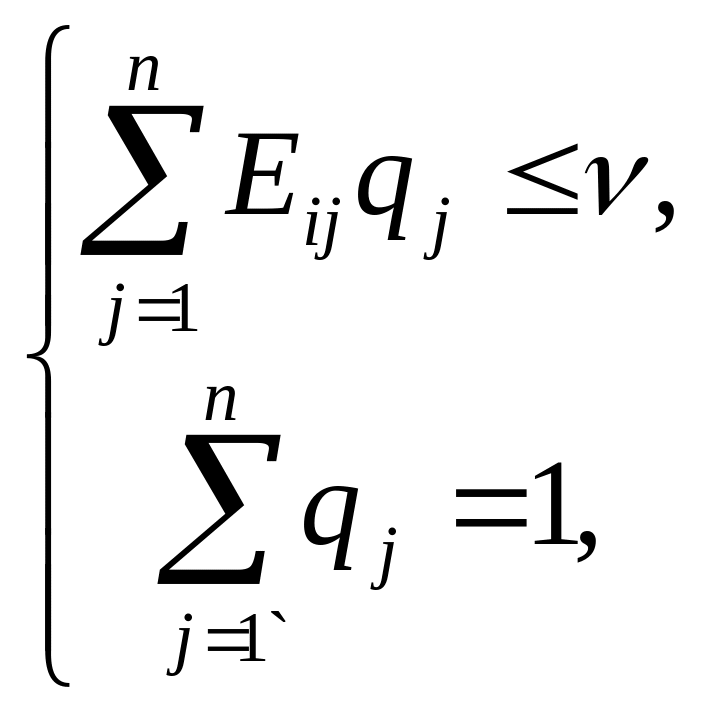
а задача линейного программирования формулируется в виде

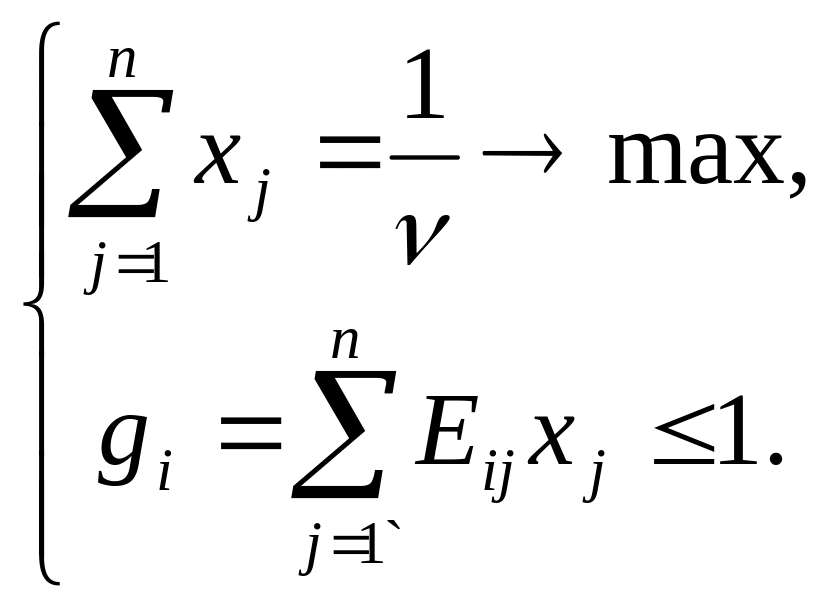
Тогда результатом решения задачи разработки управленческого решения будет последовательность наших стратегий, реализуемых по случайному закону с заданными вероятностями их появления.