Раздел 4.

Штрихи к портрету производственной функции

Современная теория производства сложилась в конце XIX-начале XX в. В явном виде производственная функция была представлена в 1890 г. английским математиком А. Берри (Berry A.The Pure Theory of Distribution // British Association of Advancement of Science : Report of the 60th Meeting, 1890. London, 1893. P. 923-924), помогавшим А. Маршаллу при подготовке математического приложения к его "Принципам экономической науки". Однако попытки установить зависимость выпуска от количества применяемых ресурсов и дать ей какое-то аналитическое выражение имели место задолго до этого. Познакомимся с некоторыми из них.

Марк Теренций Варрон против Марка Порция Катона

В трактате "О земледелии" известный римский писатель и государственный деятель Марк Порций Катон (234-149 гг. до н. э.) описывает две образцовые виллы (хозяйства): оливковую виллу и виноградник (винодельческое хозяйство). Среди множества рекомендаций по их обустройству есть и такие: для обработки оливково рощи в 240 югеров (1 югер равен примерно 3 тыс. м²) Катон определяет необходимое число рабов в 13 человек, включая вилика (управляющего) и вилику (ключницу), а для обработки виноградника в 100 югеров это число составляет 16 человек.

Нормы, предложенные Катоном, вызвали возражение у Марка Теренция Варрона (116-27 гг. до н. э.), столь же известного "писателя по земледелию". Они изложены в его трактате "О сельском хозяйстве". Варрон не соглашается с предположением Катона о том, что между площадью участка и числом рабов, необходимых для его обработки, существует прямая пропорциональная зависимость. Довод Варрона: в общее число рабов Катон не должен был включать вилика и вилику, т. е. расходы по управлению (на содержание управляющего и ключницы), ибо эти расходы постоянны и не зависят от площади участка. "Следовательно, - заключает Варрон, - должно уменьшаться или увеличиваться только число работников и погонщиков быков пропорционально уменьшению или увеличению размера имения". Но и это при условии, "если земля однородна". Если же естественные условия отдельных участков различны, то число рабов будет другим.

Видел Варрон и проблему целочисленности. Он говорил, что Катон предложил меру не единообразную и не нормальную - 240 югеров (нормой является центурия в 200 югеров). Как, "согласно его наставлению, я мог бы отнять шестую часть от 13 рабов или, оставляя в стороне вилика и вилику, каким образом я мог бы отнять шестую часть от 11 рабов?" (Античный способ производства в источниках. Л., 1933. С. 22).

Таким образом, Варрон по сути дела приходит к выводу о необходимости сопоставления затрат и выпуска как приращений соответствующих переменных, хотя понятие переменной не было, вероятно, ему известно.

Н. Г. Чернышевский

В известных дополнениях к переводу "Оснований политической экономии" Дж. С. Милля, сделанному в 1859 г. для журнала "Современник", Н. Г. Чернышевский так определил задачу экономической науки; "Разложив продукт на доли, соответствующие разным элементам производства, она должна искать, какое сочетание этих элементов и долей дает наивыгоднейший практический результат. В чем тут состоит задача - понятно каждому: надобно отыскать, при каком сочетании элементов производства данное количество производительных сил дает наибольший продукт" (Чернышевский Н. Г. Очерки из политической экономии (по Миллю) // Избр. экон. произведения : В 3-х т. М., 1949. Т. 3, ч. 2. С. 178). Более того, он предложил и "формулу зависимости производства от двух факторов" (Чернышевский Н. Г. Основания политической экономии Джона Стюарта Милля // Избр. экон. произведения : В 3-х т. М., 1948. Т. 3, ч. 1. С. 306-307), или, как сказали бы мы сейчас, производственную функцию определенного вида.

"Формула", предложенная Чернышевским, проста:

AB = C,

(9)

где А - "производительные орудия"; В - "работник"; С - "количество продукта известных качеств, производимого дневным трудом этого работника посредством этих орудий". Коэффициенты при А, Ви С характеризуют соответственно "степень достоинства" орудий и работника и "успешность производства". Однако, поскольку сумма коэффициентов при А и В характеризует "данное количество сил, могущих быть обращенными на производство", мы вправе рассматривать их как количество "орудий" и "работников" скорее, чем показатели "степени достоинства" тех и других.

Н. Г. Чернышевский приводит и числовую иллюстрацию своей формулы:

1A ∙ 19B = 19C 2A ∙ 18B = 36C ...................... 8A ∙ 12B = 96C 9A ∙ 11B = 99C 10A ∙ 10B = 100C 11A ∙ 9B = 99C 12A ∙ 8B = 96C ...................... 19A ∙ 1B = 19C

Очевидно, что "производственная функция" Чернышевского является однородной функцией второй степени. Если мы увеличим количество "орудий" и "работников" в k раз, то

С* = kAkB = k2AB.

Следовательно, производство у Чернышевского характеризуется возрастающей отдачей от масштаба.

Изокванта функции (9) имеет на графике вид равнобочной гиперболы. Карта изоквант представлена на рис. 20. Норма технической замены "орудиями" "работников" при неизменном выпуске падает (см. таблицу).

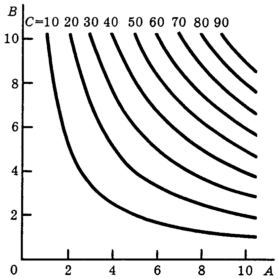  Рис. 20. Карта изоквант производственной функции Н. Г. Чернышевского для различных значений С

Норма технической замены для функции (9) при С = 10

A	B	RTSAB
10,00 5,00 3,33 2,50 2,00 1,66 1,43 1,25 1,11 1,00	1 2 3 4 5 6 7 8 9 10	- 5,00 1,60 0,83 0,50 0,34 0,23 0,18 0,14 0,11

К. Маркс

Взаимосвязь между количествами применяемых ресурсов и объемом выпуска Маркс называл техническим строением капитала. Напомним, что он различал техническое, стоимостное и органическое его строение. Если первое определяется отношением между средствами производства и необходимым для их применения количеством рабочей силы, а второе - тем отношением, в котором капитал распадается на стоимость средств производства и стоимость рабочей силы, то органическим строением капитала Маркс называл его стоимостное строение, "поскольку оно определяется его техническим строением и отражает в себе изменения технического строения" (Маркс К., Энгельс Ф. Соч. 2-е изд. Т. 23. С. 626).

Различая техническое и органическое строение, Маркс писал:

"Первое отношение покоится на техническом базисе и на известной ступени развития производительных сил может рассматриваться как данное. Требуется определенная масса рабочей силы, представленная определенным числом рабочих, чтобы произвести определенную массу продукта, например, в течение одного дня, и, следовательно, - что уже при этом само собой разумеется, - привести в движение, потребить производительно определенную массу средств производства, машин, сырья и т. д. ...Отношение это очень различно в различных отраслях производства, часто даже в различных подразделениях одной и той же отрасли промышленности, хотя, с другой стороны, в очень отдаленных друг от друга отраслях промышленности оно случайно может быть совершенно или почти одинаковым" (там же. Т. 25, ч. 1. С. 157-158).

Достаточно сравнить приведенное определение технического строения капитала с современными определениями производственной функции, чтобы убедиться в их логическом тождестве. Это дает основание использовать в качестве меры технического строения не сами массы капитала (K) и труда (L), а частные дифференциалы простейшей производственной функции Q = f(K, L):

[(Q/K)/(Q/L)]∙(K/L)

(10)

Если обозначить цену капитала Р_K, а цену труда P_L и приравнять техническое и стоимостное строение, получим

[(Q/K)/(Q/L)]∙(K/L) = (РK/PL )∙(K/L)

(11)

А это значит, что стоимостное строение капитала можно рассматривать как его органическое строение лишь в том случае, если цены ресурсов пропорциональны их предельной производительности:

РK/(Q/K) = PL/(Q/L).

(12)

Поскольку равенство (12) легко приводится к условию оптимальной комбинации ресурсов (7).

Н. Огронович

В 1871 г. в Санкт-Петербурге вышла в свет небольшая книжка с любопытным названием "Новое определение труда и капитала. Наибольшая ценность того или другого, значение наибольшей ценности их в социальной жизни и о наибольшем их производстве, или Новая наука о концентрировании атомов, клеточек, индивидов, ферм в производительных районах с приложением высшей математики". В сущности, это была даже не книга, а "Слово от автора" к будущему труду, который не появился. Автор же книги подписался так: "Н. Огронович (Кудашев, Ху-даш по матери. Воспитанник Киевского университета Св. Владимира)".

Скорее всего, как и книга Г. Госсена (см. лекцию 12, раздел 3), сие "слово" оказалось не замеченным научными кругами. А между тем в ней была сформулирована идея производственной функции практически в современном виде. Н. Огронович пишет: "Труд мой "Наука о концентрировании атомов, индивидов, ферм"... будет по преимуществу не социальный, а политико-экономический, ибо в основу войдет математическая функция, найденная для определения производства; из этой функции мы можем определить maximum и minimum функции, или наибольшее и наименьшее производство всякого организма индивидуального, всякого организма фермы и всякого другого организма. Потом будет определена прибыль, которая не что иное, как d-л. этой функции... Потом будет определена ценность из этой функции всякой производительной силы, которая есть не что иное, как прибыль, или как d-л производства этой производительной силы, помноженной на то число, какое будет показывать, сколько раз производительная сила участвовала в производстве общем в данный момент производства". С помощью этой функции Огронович хочет в своей будущей книге "определить ценность труда, ценность оборотного капитала, ценность основного капитала и ценность сил природы".

Одновременно Н. Огронович затрагивает и вопрос технического прогресса: "...прогресс производства требует, чтобы капитал все более и более беспредельно рос и разнообразился... Я буду доказывать, что производство будет самым ничтожным образом увеличиваться, если мы будем увеличивать труд, увеличивать напряжение своих мышц... и напротив того, производство наше будет сильно увеличиваться, если мы будем увеличивать капиталы - как оборотный, так и основной и реализованный. Увеличение производства требует увеличения капиталов и уменьшения количества труда. Уменьшить же количество труда - значит уменьшить запрос на труд, и ценность труда упадет" (Огронович Н. Новое определение труда и капитала. СПб., 1873. С. 3).

Таким образом, воспитанник Киевского университета задолго до работ П. Дугласа пришел к идее производственной функции (математической), выразив ее вербально. Но разве основатели австрийской школы политической экономии не сделали того же самого с функцией полезности?

Теория производства и предложения благ

Основная задача данной главы - выявить факторы, определяющие объем отраслевого предложения, т.е. суммарное предложение конкретного блага со стороны всех его производителей. При этом будем полагать, что производители, во-первых, не изменяют величину запасов готовой продукции, поэтому объемы производства и продажи товаров всегда совпадают и, во-вторых, не могут влиять на цены, которые заданы для них рынком. Фирму, которая работает в условиях заданных цен и не может повлиять на их уровень, называют конкурентной, т.е. фирмой работающей в условиях совершенной конкуренции.

Последовательность решения этой задачи представлена в левой части схемы рыночного ценообразования, приведенной в Главе 1 (см. рис. 1.3). Прежде чем доставить продукцию на рынок, ее нужно произвести. Производство продукции требует определенных затрат; их величина зависит от заданных цен факторов производства и технологии, которая предопределяется имеющимися объемами труда и капитала.

Производитель принимает хозяйственные решения, будучи ограниченным, с одной стороны, физическими условиями изготовления продукции (технологией), с другой - экономической конъюнктурой (ценами факторов производства и готовой продукции). Технологические особенности производства рассматриваются в 2.1. В дальнейшем в 2.2 и 2.3 вводятся цены, что позволяет перейти к анализу технико-экономических условий функционирования конкурентной фирмы, на основе которого в 2.4 устанавливается зависимость между объемом предложения продукции и определяющими его факторами.

 Производственная функция и техническая результативность производства

Производство есть процесс преобразования одних благ в другие: факторов производства в готовую продукцию. Зависимость между количеством используемых факторов производства и максимально возможным при этом выпуском продукции называютпроизводственной функцией.

Все факторы производства можно представить в виде трех агрегатов: труд, капитал (орудия и средства труда, включая природные ресурсы) и уровень научно-технических знаний (научно-технический прогресс). Научно-технический прогресс является основным фактором увеличения результативности современного производства, но в отличие от труда и капитала он не имеет самостоятельной вещественной формы и проявляется в виде совершенствования средств производства и повышения квалификации работников. Поскольку микроэкономика изучает процесс ценообразования как механизм согласования индивидуальных целей взаимосвязанных экономических субъектов в заданных условиях, то уровень развития НТП предполагается заданным¹. В этом случае объем выпуска продукции (Q) зависит от количества и качества только двух совместно применяемых факторов производства – труда (L) и капитала (К), т. е. производственная функция имеет вид Q = Q(L,K). Переход к новой технологии отображается изменением оператора производственной функции – характера зависимости выпуска от объемов используемых факторов производства.

Параметры производственной функции являются натуральными величинами потока, имеющими размерность количество/время. Если, например, при оптимально организованном производстве за 1 час 5 рабочих на 3 станках изготовляют 20 деталей, то Q = 20 шт/час,L = 5 часов труда, K = 3 стако-часа. Для краткости в дальнейших примерах размерность параметров будем опускать.

Конкретный вид производственной функции устанавливается на основе наблюдений за тем, как меняется объем выпуска по мере изменения применяемых объемов труда и капитала.

Короткий и длительный периоды. Возможности изменить используемые в производстве объемы труда и капитала неодинаковы. Если спрос на продукцию фирмы возрастает, то на первых порах увеличение производства достигается за счет дополнительного привлечения труда на те же производственные мощности, поскольку для расширения последних, как правило, требуется больше времени. В связи с этим вводятся понятия «короткий» и «длинный» периоды.

Время, в течение которого нельзя изменить объем одного из используемых в производстве факторов, называют коротким периодом. В свою очередь фактор, объем которого нельзя изменить в коротком периоде называют постоянным, а фактор, объем использования которого меняется по мере изменения выпуска, - переменным. Время, достаточное для изменения объемов обоих факторов производства, - это длинный период, и поэтому в нем все факторы являются переменными.

Соотношение между количеством выпускаемой за определенное время продукции (output) и количеством используемых для ее изготовления факторов производства (input) назовем технической результативностью производства. В коротком и длинном периодах она измеряется по-разному.

 Затраты производства и функция затрат

Затраты - это ценность материалов и услуг факторов производства, использованных при изготовлении продукции. Поскольку материалы, потребленные в данном процессе производства, ранее были изготовлены при использовании труда и капитала, то в итоге все затраты сводятся к оплате факторов производства.

Когда объем производства превышает единицу, тогда различают общие затраты ТС (total cost) на весь выпуск, средние затраты АС (average cost) на единицу продукции (АС = TC/Q) и предельные затраты МС (marginal cost) - приращение общих затрат при увеличении выпуска на единицу (МС =  TC/ Q).

Зависимость между объемом произведенной продукции и минимально необходимыми для ее производства затратами называют функцией затрат.

Обозначим цену труда, т.е. количество денег, которое необходимо заплатить за использование наемного работника в течение определенного времени, r_L, а цену капитала - количество денег, уплачиваемое за применение средств производства в течение некоторого времени, - r_K. Тогда общие затраты на выпуск некоторого количества продукции: TC = r_LL + r_KK.

При заданных ценах факторов производства величина затрат определяется минимально необходимыми для выпуска продукции объемами труда и капитала, т.е. технологией, представленной производственной функцией Q = Q(L,K). Поэтому L = L(Q), K = K(Q), а следовательно, и TC = TC(Q).

Выделение короткого и длинного периодов при построении производственной функции находит свое отражение и в функции затрат. Поскольку в коротком периоде К =   = const, то функция затрат в этом случае имеет вид TC(Q) = r_LL(Q) + r_K , т.е. в коротком периоде затраты делятся на постоянные TFC (total fixed cost), не зависящие от объема выпуска (TFC = r_K ), и переменные TVC (total variable cost), меняющиеся по мере изменения выпуска (TVC = r_LL(Q)). В длинном периоде все затраты переменные.

Переход от производственной функции к функции общих затрат осуществляется в приведенной ниже последовательности:

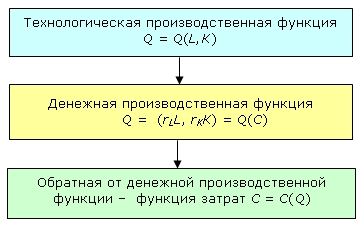
Выполним этот переход графически и алгебраически для короткого и длинного периодов.

 Прибыль и условия ее максимизации

Произведение объема проданной продукции на ее цену называют общей выручкой TR - (total revenue). Разность между общей выручкой и общими затратами есть прибыль.

Цель конкурентной фирмы - получить максимум прибыли. Если у фирмы разность между выручкой и затратами будет меньше, чем у конкурентов, то со временем ее вытеснят с рынка. Поэтому конкурентная фирма производит и предлагает на рынке такой объем продукции, который максимизирует ее прибыль.

При экзогенно заданной системе цен прибыль зависит только от объема выпуска

(Q) = PQ - TC(Q),

где Р - цена блага.

В этом случае необходимым условием ее максимизации является следующее равенство:

а достаточным - отрицательное значение второй производной функции прибыли:

<0.

Рис. 2.21. Выпуск, максимизирующий прибыль конкурентной фирмы

Достаточное условие выполняется, если предельные затраты возрастают. Следовательно, прибыль конкурентной фирмы достигает максимума при таком объеме выпуска, при котором возрастающие предельные затраты становятся равными цене продукции (рис. 2.21). Расстояние между линиями Р и АС представляет величину средней прибыли при выпуске Q единиц продукции. Прибыль достигает максимума при выпуске Q* единиц продукции. Обратим внимание на то, что при выпускеQ0 единиц предельные затраты тоже равны цене, но здесь не выполняется достаточное условие максимизации прибыли. Максимальная сумма прибыли равна площади заштрихованного прямоугольника.

Объем выпуска, максимизирующий прибыль, зависит от технологических и экономических условий функционирования фирмы. Первые отображаются кривой общего выпуска (см. рис. 2.1), а экономические условия можно представить линией равной прибыли илиизопрофитой. Уравнение изопрофиты выводится из уравнения прибыли

,

где  ₀ - заданная величина прибыли.

Каждая точка изопрофиты указывает на такое сочетание Q, L, которое обеспечивает заданный объем прибыли. Каждому объему прибыли соответствует своя изопрофита (рис. 2.22).

Рис. 2.22. Изопрофиты

Рис. 2.23. Технологические и экономические условия максимизации прибыли

Наложение карты изопрофит на кривую общего выпуска (рис. 2.23) совмещает технологические и экономические условия работы фирмы. Точка касания кривой TP_L с наиболее высокорасположенной изопрофитой определяет объем выпуска, максимизирующий прибыль в сложившихся условиях.

Функция предложения и излишек производителя

Функция предложения выражает зависимость между количеством предлагаемых благ и факторами, определяющими это количество. Так как фирма предлагает объем выпуска, максимизирующий прибыль, то функция предложения выводится из условия максимизации прибыли: функция предложения является обратной к функции, выражающей условие максимизации прибыли. Выведем ее для конкурентной фирмы, работающей по технологии Q = L K . Соответствующая ей функция общих затрат в длинном периоде представлена формулой (2.7); ее производная по выпуску представляет предельные затраты

.

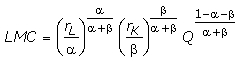Приравняв предельные затраты к цене продукции и решив полученное уравнение относительно объема выпуска, получим функцию предложения фирмы в длинном периоде

.

Рис. 2.24. Построение кривой предложения конкурентной фирмы в длинном периоде

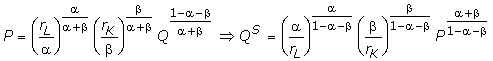Таким образом, в длинном периоде объем предложения конкурентной фирмы при заданной технологии определяется только системой (вектором) цен: QS = QS(rL, rK, P). Графическое построение функции предложения показано на рис. 2.24. При цене P1 фирма, чтобы получить максимум прибыли, предложит Q1 единиц продукции; при цене P2 она произведет Q2 единиц и т.д. Если цена опустится ниже P1, то фирма прекратит производство данного блага, так как его цена не покрывает всех затрат. Следовательно, участок кривой LMC, идущий вверх от пересечения с кривой LAC, и есть график функции предложения по цене в длинном периоде: QS = QS(P). Изменение цен факторов производства отображается сдвигом кривых затрат, а потому и кривой предложения по цене.

В коротком периоде при рассматриваемой технологии функция общих затрат представлена формулой (2.3). Ей соответствует следующая функция предельных затрат:

,

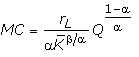а функция предложения выводится из равенства

.

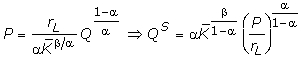Рис. 2.25. Построение кривой предложения конкурентной фирмы в коротком периоде	Кроме цен, объем предложения фирмы в коротком периоде зависит от заданного объема капитала: QS = QS(rL, P,  ). Из-за того, что в коротком периоде затраты делятся на постоянные и переменные, кривая предложения в коротком периоде начинается с точки пересечения кривой предельных затрат с кривой средних переменных затрат (рис. 2.25). Когда цена на продукцию фирмы находится в интервале P0, P1, тогда выручка фирмы меньше общих затрат; но поскольку цена возмещает переменные затраты, то фирма может некоторое время (пока не требуется возмещать постоянные затраты) производить продукцию. П роцесс максимизации прибыли и выведение функции предложения конкурентной фирмы иллюстрирует   2.12.
Равновесие производителя
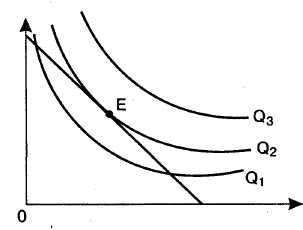
Равновесие производителя - состояние производства, при котором использование факторов производства позволяет получить максимальный объем продукции, т. е. когда изокванта занимает самую отдаленную от начала координат точку. Чтобы определить равновесие производителя, необходимо совместить карты изоквант с картой изокост. Максимальный объем выпуска будет в точке касания изокванты с изокостой (рис. 21.6). Рис. 21.6. Равновесие производителя Из рис. 21.6 видно, что изокванта, расположенная ближе к началу координат, дает меньшее количество производимой продукции (изокванта Q1). Изокванты, расположенные выше и правее изокванты Q2, вызовут изменение большего объема факторов производства, нежели позволяет бюджетное ограничение производителя. Таким образом, точка касания изокванты и изокосты (на рис. 21.6 точка Е) является оптимальной, поскольку в этом случае производитель получает максимальный результат.