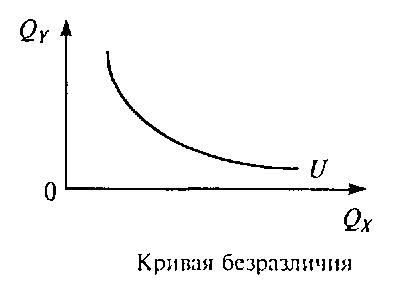
Кривая безразличия

Наибольший вклад в разработку ординалистской (порядковой) полезности внесли Ф.Эджуорт, В. Парето, Е. Слуцкий, Р. Аллен и Дж. Хикс. Эти ученые предложили измерять субъективную полезность с помощью не абсолютной (кардиналистская теория), а относительной шкалы, показывающей предпочтение потребителя (ординалистская теория). При этом потребителю необходимо лишь сделать выбор между двумя наборами потребительских благ (2 блага рассматриваются в целях упрощения).

Кривая безразличия показывает различные комбинации 2-х экономических благ, имеющих одинаковую полезность для потребителя.

На рис.4.1(а) показана кривая безразличия (U). По осям откладывается количество блага Х и блага Y, между которыми делает выбор потребитель.

Множество кривых безразличия называется картой кривых безразличия (рис.4.1б). Чем правее и выше расположена кривая безразличия, тем больше удовлетворения приносят представленные ею комбинации благ. Кривые безразличия имеют отрицательный наклон, выпуклы относительно начала координат и никогда не пересекаются друг с другом. Поэтому через любую точку можно провести лишь 1 кривую.

Зона замещения (субституции) – участок кривой безразличия, в котором возможна эффективная замена одного блага другим.

На кривой безразличия зона замещения обозначена отрезком RS (рис.4.2а). Взаимная замена благ Х и Y имеет смысл только в пределах отрезка RS. Вне отрезка замена исключается. Два блага выступают как независимые друг от друга.

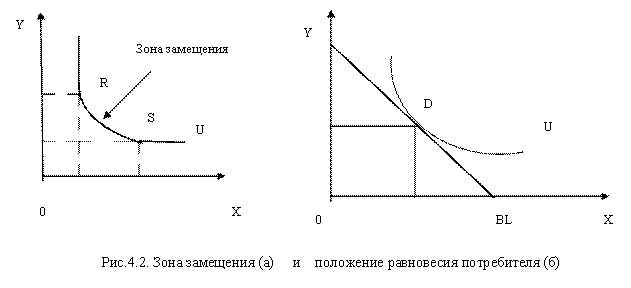
Предельная норма замещения (MRS) – количество, на которое потребление одного из 2-х благ должно быть увеличено (уменьшено), чтобы полностью компенсировать потребителю уменьшение (или увеличение) потребления другого блага на одну дополнительную (предельную) единицу.

 

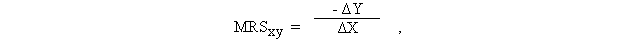
где MRS_хy - предельная норма замещения (субституции) блага Y на Х.

Кривые безразличия и их свойства

Предположим, что потребитель имеет набор благ, состоящий из X и Y. Все соотношения количеств этих благ для него равноценны, потребителю безразлично, какой набор выбрать. Следовательно, эти товары принадлежат к набору безразличия. Набор безразличия — набор вариантов потребительского выбора, каждый из которых обладает одинаковой полезностью и поэтому не имеет предпочтения перед другими.

Кривая безразличия является графическим отображением набора безразличия. Кривая безразличия— совокупность наборов благ, обеспечивающих потребителю равный объем удовлетворения потребностей, т. е. приносящих ему одинаковую полезность. Взяв другие возможные сочетания благ, соответствующие различным величинам совокупной полезности, можно составить карту безразличия.Карта безразличия — совокупность кривых безразличия, соответствующих различным уровням полезности для одного потребителя и одной пары благ. Вкусы и предпочтения потребителя представляются картой кривых безразличия. Каждая следующая кривая безразличия, проходящая дальше от начала координат, предполагает относительно большую величину полезности.

Любая кривая безразличия представляет одинаковую совокупную полезность различных благ для потребителя. Кривая безразличия (U) состоит из точек, символизирующих наборы то­варов Х и Y. Совокупные полезности всех наборов, представленные точками на этой кривой одинаковы, т. е. потребителю безразлично, какую именно комбинацию товаров Х и Y он приобретет. Переходя от точки А к точке В, потребитель сокращает потребление блага Y на ΔY и наращивает потребление товара X на ΔХ, но общий уровень удовлетворения потребителя (совокупная полезность) остается неизменным (рисунок ниже).

Зона замещения (субституции) — участок кривой безразличия, на котором возможна эффективная замена одного блага другим.

Взаимная замена благ X и Y возможна только в пределах отрезка АВ (зоне замены). Количество блага Х₁представляет минимально необходимое количество потребления блага X, от которого потребитель не может отказаться, как бы много товара Y ни предлагалось взамен. Аналогично Y₁ — минимально необходимое количество потребления блага Y. Предельная норма замещения — норма, в соответствии с которой одно благо может быть заменено другим благом без выигрыша или потери полезности для потребителя. Предельная норма замещения — количество одного блага, от которого потребитель готов отказаться, чтобы получить дополнительную единицу другого блага. Предельная норма замещения рассчитывается следующим образом:

где MRS — предельная норма замещения; Q_x — количество това­ра X; Q_Y — количество товара Y.

Предельная норма замещения всегда отрицательная величина, так как прирост потребления одного блага происходит за счет сокращения потребления другого. Предельная норма замещения уменьшается при движении вдоль кривой безразличия — получая в свое распоряжение все большее количество данного блага и наращивая его потребление, покупатель в обмен готов отказаться от все меньшего количества другого блага, которое становится все более дефицитным. У потребителя, желающего остаться на той же кривой безразличия, прирост полезности от наращивания потребления блага X должен быть равен потере полезности от сокращения потребления товара Y. Таким образом, предельная норма замещения блага X благом Y может рассматриваться как отношение предельной полезности блага X к предельной полезности блага Y:

Рассмотрим некоторые свойства кривых безразличия:

• кривые безразличия имеют отрицательный наклон. Между количествами благ X и Y существует обратная связь. При уменьшении потребления одного блага, для компенсации потерь и сохранения прежнего уровня полезности, потребитель должен увеличить потребление другого блага. Любая кривая, выражающая обратную связь переменных, имеет отрицательный наклон;

• кривые безразличия выпуклы по отношению к началу координат. Выше отмечалось, что при увеличении потребления одного блага потребитель должен уменьшить потребление другого блага. Выпуклость кривой безразличия по отношению к началу координат является следствием падения предельной нормы замещения. Пологий спуск кривой безразличия вниз или подъем наверх свидетельствует об убывании темпов замещения одного блага другим по мере уменьшения доли данного блага в потребительской корзине;

• абсолютная величина наклона кривой безразличия равна предельной норме замещения. Угол наклона кривой безразличия в данной точке показывает норму, в соответствии с которой одно благо может быть заменено другим благом без выигрыша или потери полезности для потребителя. Данное соотношение характеризуется предельной нормой замещения;

• кривые безразличия не пересекаются. Один и тот же потребитель не может характеризовать один и тот же набор благ различными уровнями полезности. Следовательно, две кривые безразличия, представляющие различные уровни полезности, не могут пересечься;

• возможно построить кривую безразличия, проходящую через любой набор благ. Кривую безразличия можно построить для любой пары благ, приносящих определенный уровень полезности. Именно по этому принципу строится карта безразличия, дающая полную информацию о системе предпочтений потребителя.

Кривые безразличия

Прежде всего, очевидно, нам необходимо создать некий графический образ пространства благ, чтобы обеспечить возможность графического изображения любого из возможных наборов благ. Заметим, что графические методы наряду со своими неоспоримыми достоинствами имеют и один весьма существенный недостаток: эти методы ограничивают исследователя двумерным пространством. Оказывается, однако, что основные выводы, полученные для случая двух благ, без труда могут быть распространены и на случай сколь угодно большого числа благ.

Именно последнее обстоятельство и дает нам возможность "пожертвовать" количеством благ с целью большей наглядности и доступности изложения.

Итак, пусть потребитель сталкивается только с двумя благами, Х и У. Тогда любая из возможных комбинаций благ (например, комбинация А, содержащая х, единиц блага Х и у₁ единиц благ Y) может быть представлена в виде точки на графике (рис. 1), где по оси абсцисс откладывается количество единиц блага X, а по оси ординат - количество единиц блага Y.

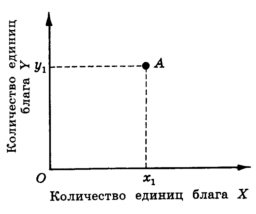Рис. 1 Пространство благ

Основная идея графического представления системы предпочтений (функции полезности) потребителя с помощью кривых безразличия (впервые примененных английским экономистом Ф. Эджуортом в 1881 г.) весьма проста: соединим все точки, характеризующие наборы благ, имеющие некоторый определенный уровень полезности (для потребителя но, какой их этих наборов выбирать), и назовем полученную линию равной полезности кривой безразличия. Повторим теперь то же самое с наборами благ, имеющими какой-либо иной уровень полезности. Проделав эту операцию со всеми возможными наборами благ, получим карту безразличия - множество кривых безразличия, соответствующих всем возможным уровням полезности для данного потребителя. Очевидно, карта безразличия есть не что иное, как графическое изображение шкалы предпочтений потребителя.

Рассмотрим теперь некоторые свойства кривых безразличия.

Свойство 1. Кривые безразличия имеют отрицательный наклон.

Попробуем определить, в какой области лежат точки, характеризующие комбинации благ, имеющие такой же уровень полезности, как и набор А (рис. 2). Для этого проведем параллельно осям координат две перпендикулярные прямые линии, пересекающиеся в точке А. Эти линии разделяют пространство благ на четыре квадранта. Очевидно, что в соответствии с предположением III ординалистской теории полезности ("больше - лучше, чем меньше") любой набор благ из квадрантаI предпочтительнее набора А. По этой же причине набор А предпочтительнее любого набора из квадранта III. Следовательно, все наборы благ, имеющие равный с набором А уровень полезности, должны лежать в квадрантах II и IV. Иными словами, кривая безразличия имеет отрицательный наклон. Это обстоятельство вполне понятно - ведь чтобы сохранить тот же общий уровень полезности набора при уменьшении потребления благ X, потребитель должен компенсировать это уменьшение увеличением потребления благ Y.

Рис. 2. Кривые безразличия имеют отрицательный наклон

Предположение III приводит нас к еще одному важному выводу: все точки, лежащие выше данной кривой безразличия, характеризуют наборы благ, имеющие более высокий уровень полезности, чем лежащие на этой кривой безразличия, а точки, лежащие ниже данной кривой безразличия, — наборы, имеющие более низкий уровень полезности. (Предоставим доказательство читателю).

Свойство 2. Две кривые безразличия не могут пересекаться.

Предположим, что две кривые безразличия пересекаются в точке А (рис. 3).

Рис. 3. Кривые безразличия не могут пересекаться

Тогда (по определению кривой безразличия) B ~ A, C ~ A.

Следовательно, по предположению II (транзитивности) должно быть B ~ C

Но это неверно. На самом деле (по предположению III) B > C.

Следовательно, две кривые безразличия не могут иметь общую точку, так как один набор благ не может характеризоваться двумя различными уровнями полезности.

Свойство 3. Кривая безразличия может быть проведена через каждую точку в пространстве благ (по предположению I о сравнимости). Таким образом, мы получаем множество кривых безразличия - карту безразличия (рис. 4), содержащую полную информацию о системе предпочтений потребителя.

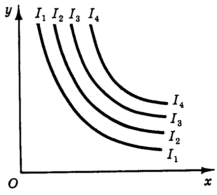Рис. 4. Карта безразличия

Обращаем внимание читателя, что мы до сих пор изображали кривые безразличия выпуклыми к началу координат, ничем не аргументируя принятие такой формы кривых безразличия. Заметим также, что выпуклость не может быть обоснована предположениями I-III ординалистской теории полезности, т. е. требует от нас некоторых дополнительных предположений.

Попробуем теперь объяснить, почему мы изображаем кривые безразличия выпуклыми к началу координат.

Пусть x₁x₂ = x₃x₄ (рис. 5). Тогда при переходе из точки А в точку В потребитель сохранил общую полезность набора благ при увеличении потребления блага Х на x₁x₂ единиц и уменьшении потребления блага Y на y₁y₂ единиц. При переходе из точки С в точку D потребитель сохранил общую полезность при увеличении потребления блага Х на x₃x₄ = x₁x₂ единиц и уменьшении потребления блага Y на y₃y₄ единиц; при этом y₁y₂ > y₃y₄.

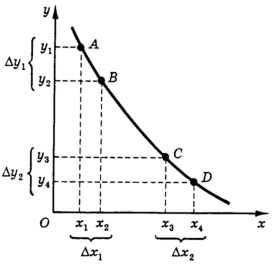Рис. 5. Уменьшение нормы замены при движении по кривой безразличия

Введем теперь понятие нормы замены. Нормой замены блага Yблагом Х называется то количество блага Y, которое потребитель согласен уступить "в обмен" на увеличение количества блага Х на единицу с тем, чтобы общий уровень удовлетворения остался неизменным:

RS = - y/x.

(7)

Из рис. 5 видно, что норма замены уменьшается при движении вдоль кривой безразличия, что, впрочем, вполне объяснимо логически: с увеличением количества блага Х и, соответственно, уменьшением количества блага Y потребитель все больше ценит ставшее относительно более дефицитным благо Y и, следовательно, готов отдать все меньшее количество единиц этого блага в обмен на каждую следующую единицу блага X.

При приближении точки В к точке А мы получаем предельную норму замены:

RS = - y/x.

(8)

Очевидно, что предельная норма замены в этом случае равна угловому коэффициенту наклона касательной к кривой безразличия в точке А.

Таким образом, предположение о падении предельной нормы замены при движении вдоль кривой безразличия приводит нас к утверждению о выпуклости кривой безразличия: если верно первое, то верно и второе.

Итак, сформулируем еще одно свойство кривых безразличия.

Свойство 4. Предельная норма замены уменьшается при движении вдоль кривой безразличия. Кривые безразличия выпуклы к началу координат.

Строго говоря, это условие может иногда не соблюдаться. Рассмотрим два следующих случая: жесткая взаимодополняемость благ (правый и левый ботинок) и совершенная взаимозаменяемость (например, два сорта аспирина для потребителя, не видящего разницы между этими сортами).

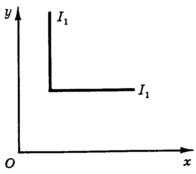  Рис. 6. Жесткая взаимодополняемость MRS = 0

На рис. 6 изображена кривая безразличия в случае жесткой взаимодополняемости, когда благ связаны в потреблении жестким соотношением и MRS = 0. На рис. 7 представлен случай совершенной взаимозаменяемости, когда оба блага воспринимаются потребителем как один, и MRS - постоянная величина.

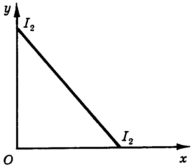  Рис. 7. Совершенная взаимозаменяемость MRS = const.

Все же мы считаем, что большинство реальных кривых безразличия лежит между этими двумя крайними случаями (при этом чем более взаимозаменяемы блага, тем менее выпуклы кривые безразличия), и четвертое свойство кривых безразличия справедливо.

Итак, карта безразличия - множество кривых безразличия (отвечающих свойствам 1-4) - дает нам полную информацию о системе предпочтений потребителя (не требуя даже присвоения полезностям наборов благ каких-либо численных значений).

Бюджетное ограничение

БЮДЖЕТНОЕ ОГРАНИЧЕНИЕ

Кривые безразличия отражают предпочтения потребителя, то есть его потребности. Помимо этого при анализе потребительского выбора следует принимать во внимание его возможности, т.е. бюджетное ограничение. Бюджетное ограничение характеризует реальную покупательную способность потребителя (I) с учетом величины и соотношения цен покупаемых товаров. Графически бюджетное ограничение выражается в виде бюджетной линии – отрезка прямой, все точки на которой показывают комбинации благ, которые потребитель в состоянии приобрести при данных ценах при полном расходовании его дохода. Угол наклона бюджетной линии (tg ) определяется обратным отношением цен товаров (PF/PC).

Изменение дохода вызывает сдвиг бюджетной линии вправо–вверх при росте дохода I и влево–вниз при его снижении. Изменение цены одного из благ потребительской корзины меняет соотношение цен товаров, а, следовательно, и угол наклона бюджетной линии.

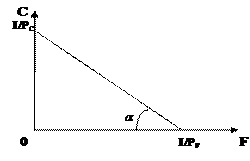
PF*F – затраты на питание;

PC*C – затраты на одежду.

Максимальные комбинации продуктов, которые потребитель может купить, лежит на прямой:

PF*F + PC*C = I

Каким количеством одежды надо пожертвовать, чтобы получить какое-то количество продуктов питания?

Для ответа на этот вопрос решим уравнение относительно С:   , где  – начальная точка ординат,   – угловой коэффициент (tg ).

Выбор между покупкой продукта и расходами на все другие блага характеризуется формулой расширенного бюджетного ограничения:

I = PXQX + å PYi*QYi , где I – располагаемый доход;

PXQX – расходы на товар Х

å PYi*QYi – сумма расходов на все остальные товары.