2. Повнота і замкненість систем булевих функцій. Теорема (критерій) Поста.

Означення 1. Булевою називається функція, яка, як і її аргументи, набувають значень лише 0 або 1.

Від однієї змінної можна побудувати чотири булеві функції: тавтологію, фальш, тотожну функцію f(x)=x та заперечення 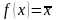. Встановлено, що від п змінних можна побудувати 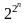різних булевих функцій. Так, наприклад, таблицею істинності можна задати 16 різних булевих функцій від двох змінних:

x1	х2	F1	F2	F3	F4	F5	F6	F7	F8	F9	F10	F11	F12	F13	F14	F15	F16
0	0	0	0	0	0	1	0	0	1	0	1	1	0	1	1	1	1
0	1	0	0	0	1	0	0	1	0	1	0	1	1	0	1	1	1
1	0	0	0	1	0	0	1	0	0	1	1	0	1	1	0	1	1
1	1	0	1	0	0	0	1	1	1	0	0	0	1	1	1	0	1

Булеві функції від двох змінних добре досліджені і мають важливе практичне значення, наприклад, для суперпозицій функцій.

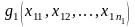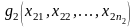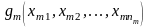Означення 2. Суперпозицією булевих функцій , ,…, в булеву функцію f(x₁, x₂,…, x_m) називається нова булева функція, яка одержується з функції f(x₁, x₂,…, x_m) в результаті підстановки замість змінних x₁, x₂,…, x_m відповідно функцій , ,…, .

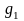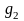В булевій логіці діє принцип суперпозиції, який стверджує, що будь‑яку складну функцію можна подати у вигляді сукупності елементар­них функцій від двох аргументів.

Наприклад: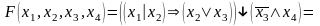

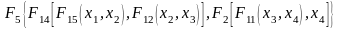
Означення 3. Система булевих функцій називається функціонально повною, якщо будь-яка булева функція може бути записана у вигляді формули че­рез функції цієї системи.

Наприклад, функціонально повною для булевих функцій від двох змінних є система, що складається з трьох функцій: кон’юнкції, суми Жегалкіна та тотожної одиниці.

З’ясувати питання функціональної повноти можна за допомогою тео­реми Поста.

Означення 4. Говорять, що функція f зберігає 0, якщо f(0,0,…,0) = 0. Позначають клас всіх булевих функцій, які зберігають нуль, через Р₀.

Оскільки 00=0 і 00=0, то кон’юнкція та диз’юнкція зберігають нуль, а еквівалентність та імплікація не зберігають, бо 00=1 і 00=1.

Означення 5. Говорять, що функція f зберігає 1, якщо f(1,1,…,1) = 1. Позначають клас всіх булевих функцій, які зберігають одиницю, через Р₁.

Очевидно, що кон’юнкція, диз’юнкція, еквівалентність та імплікація зберігають одиницю. Заперечення не зберігає одиниці так само, як не зберігає і нуль.

Означення 6. Булева функція називається лінійною, якщо її можна подати у вигляді поліному Жегалкіна першого степеня. Позначають клас всіх булевих лінійних функцій через L.

Встановити лінійність дещо складніше. Тут за звичай виконують перетворення функції в поліном Жегалкіна, причому це представлення єдине. Наприклад, =1х; xy= xy; xy = y = 1xy. Отже, з наведених функцій лише кон’юнкція не лінійна.

Означення 7. Булева функція f ^* називається двоїстою (спряженою) для функції f, якщо f ^*(x₁,x₂,…,x_n) = для будь-яких x₁,  x₂,…,  x_n. Булева функція називається самодвоїстою (самоспряженою), якщо f ^*= f . Позначають клас всіх булевих самодвоїстих функцій через S.

Якщо , то 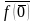= = = 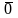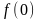і =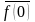 = = 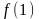. Отже заперечення є самоспряженою функцією. Оскільки 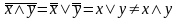, кон’юнкція не є самоспряженою функцією.

Означення 8. Говорять, що функція f монотонна, якщо з нерівностей x₁  y₁, x₂  y₂,…, x_n  y_n випливає, що f(x₁,x₂,…,x_n)  f(y₁,y₂,…,y_n). Познача­ють клас всіх булевих монотонних функцій через М.

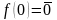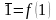Очевидно, що заперечення не є монотонною функцією, бо 0<1, але =1>0= . Оскільки 00=01=10=0<1=11, то кон’юнкція є монотонною функцією.

Означення 9. Клас булевих функцій називається власним, якщо він не порожній і не співпадає з множиною всіх булевих функцій.

Розглядаючи приклади функцій після означення кожного з класів Р₀, Р₁, L, S, М, ми наводили для кожного з них приклади функцій, які належать і які не належать кожному з цих класів. Отже ми довели теорему:

Теорема. Класи Р₀, Р₁, L, S, М є власними класами булевих функцій.

Означення 9. Клас булевих функцій називається замкнутим або класом Поста, якщо він разом зі всіма своїми функціями містить будь-яку їх суперпозицію.

Розглядаючи для кожного класу все можливі суперпозиції, встановлено, що класи Р₀, Р₁, L, S, М є класами Поста, тобто замкнутими класами.

Виходячи з цих фактів, доведено таку теорему, яка має практичне значення (хоч користуватися нею не так вже й зручно):

Теорема Поста. Система булевих функцій функціонально повна тоді і тільки тоді, коли в цій системі є функція, яка не належить класу Р₀, є функція, яка не належить класу Р₁, є функція, яка не належить класу L, є функція, яка не належить класу S, є функція, яка не належить класу M.

Користуючись теоре­мою Поста, можна стверджувати, що, наприклад, система із двох функцій кон’юнкції та заперечення є функціонально повною.

Білет 29