Действие ударной силы на мт

П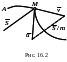 усть на МТ массой действует ударная сила и конечная сила . Время действия ударной силы назовем , скорость точки в начале удара – , а в конце (рис. 16.2).

Применим теорему об изменении количества движения МТ в интегральной форме

, (16.5)

где - ударный импульс, - импульс конечной силы.

На основе теоремы о среднем значении можно положить

, (16.6)

где - конечная величина, а - очень малая величина. Поэтому можно считать .

Тогда выражение (16.5) выглядит

, (16.7)

то есть изменение количества движения МТ за время удара равно ударному импульсу, приложенному к ней.

Выражение (16.7) называется основным уравнением динамики МТ при ударе.

Скорость МТ в конце удара

, (16.8)

здесь - конечная величина, так как , – величины конечные.

Путь МТ при ударе имеет пренебрежимо малую величину , где - переменная скорость в промежутке времени (0, ). По теореме о среднем значении

где - конечная величина, а - очень мало, поэтому

Выводы

1. При ударе действием конечных сил можно пренебречь.

2. Перемещение МТ при ударе пренебрежимо мало.

3. Действия ударных сил на МТ выражается в быстром изменении величины и направления скорости точки – формула (16.8).

Теорема об изменении количества движения системы

Пусть имеется система МТ, на которую действуют внешние и внутренние ударные силы. Действием конечных сил пренебрегаем. Время действия ударных нагрузок обозначим через . Назовем скорость -той точки в начале удара , в конце удара , равнодействующие ударных сил , внутренних сил .

По теореме об изменении количества движения при ударе для к-той точки имеем

.

Тогда для системы

,

или

(16.9)

где - количество движения системы, - внешний ударный импульс.

Теорема: изменение количества движения системы за время удара равно векторной сумме внешних ударных импульсов, приложенных к системе.

В проекциях

,

, (16.10)

.

На основании (16.4) можно получить теорему о движении центра масс системы при ударе. Известно, что в начале удара , а в его конце . Тогда

. (16.11)

В проекциях

,

, (16.12)

.

Если , то , то есть . Таким образом, если векторная сумма внешних ударных, приложенных к системе, равна нулю, то количество движения системы и скорость ее центра масс при ударе не изменяется.

Удар шара о неподвижную поверхность. Коэффициент восстановления

Пусть МТ (шарик) ударяется о гладкую неподвижную поверхность со скоростью (рис. 16.3). Найдем скорость в конце удара, если упругие свойства поверхности характеризуются коэффициентом восс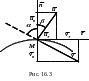 тановления .

На рисунке: Мn – нормаль к поверхности - касательная к поверхности; - угол между скоростью и нормалью (угол падения); - угол между вектором и нормалью (угол отражения).

По теореме об изменении количества движений МТ при ударе

, (16.13)

где - ударный импульс реакции, направленный по нормали в случае гладкой поверхности.

В проекциях эта теорема выглядит

,

(16.14)

.

При наличии ударного трения поверхности . Если поверхность гладкая и трение отсутствует, то (касательная составляющая скорости при ударе не изменяется) и .

Система уравнений (16.14) содержит две неизвестные и .

Для их определения используем дополнительные условия. Нормальная составляющая скорости за фазу деформации изменяется в пределах от до 0, а за фазу восстановления от 0 до .

Тогда теорема об изменении количества движения в проекции на нормаль имеет вид

откуда коэффициент восстановления

. (16.15)

Это кинематическое выражение коэффициента восстановления в случае удара. Значение положительно, так как проекции и имеют разные знаки.

Для определения и напишем систему уравнений

(16.16)

откуда находим

. (16.17)

Величина скорости МТ после удара

. (16.18)

При (абсолютно упругий удар) .

Заметим, что

, (16.19)

то есть отношение тангенса угла падения к тангенсу угла отражения равно коэффициенту восстановления.

Для опытного определения коэффициента восстановления существует много способов. Исключая влияние формы соударяющихся тел и их скорости при ударе на коэффициент восстановления, рассмотрим случай падения шарика без начальной скорости с высоты h на гладкую горизонтальную плиту (рис. 16.4). Материал шарика и плиты одинаковы.

П осле удара шарик поднимется на высоту .

По формуле Галилея

, ,

тогда

. (16.20)

Коэффициента восстановления справочная величина, зависит от материалов соударяемых тел. Например, для удара стали о сталь