Вращательное движение тела вокруг неподвижной оси

Пусть тело вращается вокруг неподвижной оси z с угловой скоростью ω (рис. 10.1).

Н апишем теорему об изменении кинетического момента системы

. (10.2)

Реакции опор А и В являются внешними силами, но они пересекают ось вращения и момента относительно нее не дают. Поэтому в выражении ∑M_z^(е) входят только моменты внешних сил.

Подставив в выражение (10.2) значение кинетического момента в виде

,

получим

.

Так как , то

,

или

. (10.3)

Получено дифференциальное уравнение вращательного движения твердого тела вокруг неподвижной оси.

При сравнении этого уравнения с дифференциальными уравнениями (10.1) поступательного прямолинейного движения твердого тела видно, что момент инерции при вращении твердого тела играет ту же роль, что и его масса при поступательном движении.

С помощью дифференциального уравнения вращательного движения твердого тела можно решать такие задачи.

1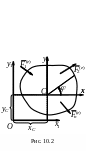 . По заданному закону вращения и моменту инерции тела можно определить главный момент внешних сил, действующих на тело,

.

2. По заданным внешним силам и моменту инерции тела можно найти уравнение вращательного движения .

3. По величинам и можно определить момент инерции тела .

Плоское движение

Пусть твердое тело совершает плоское движение так, что центр масс С движется в плоскости чертежа (рис. 10.2). В динамике за полюс принимается центр масс тела, а не произвольная точка (как в кинематике).

Уравнение движения плоской фигуры

, , . (10.4)

При известных силах дифференциальные уравнения плоского движения твердого тела выглядят

,

, (10.5)

,

где - проекции главного вектора внешних сил на координатные оси, - главный момент внешних сил относительно оси , перпендикулярной к плоскости чертежа.

Третье из этих уравнений выводится аналогично дифференциальному уравнению вращательного движения твердого тела относительно неподвижной оси.

Решением системы (10.5) с использованием начальных условий находятся уравнения плоского движения твердого тела.

Если траектория центра масс задана, то удобно использовать дифференциальные уравнения движения точки С в проекциях на естественные координатные оси

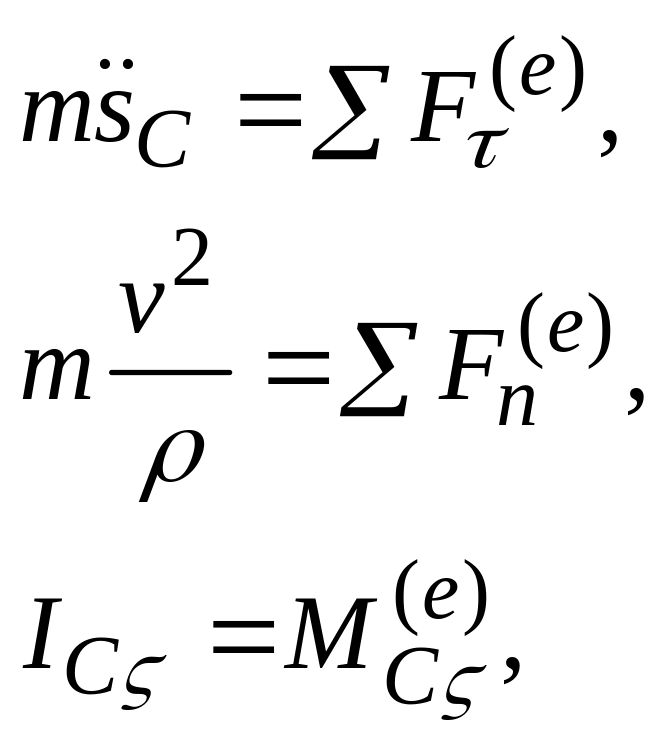(10.6)

где s_c - путь центра масс, v_c - его скорость, - радиус кривизны его траектории.

Физический маятник

Это твердое тело, имеющее горизонтальную ось вращения, не проходящую через его центр тяжести и находящееся под действием только силы тяжести (рис. 10.3). Ось вращения физического маятника называется осью привеса маятника.

Пусть ось привеса проходит через точку О, то есть является осью x (плоскость движения центра тяжести С совпадает с координатной плоскостью yOz). Тогда дифференциальное уравнение вращательного движения маятника имеет вид

(реакции Z₀, Y₀ момента не дают, а моментом силы трения в шарнире О пренебрегаем).

Здесь J_х - момент инерции маятника относительно оси привеса, G=Мg – вес маятника, d - расстояние от центра тяжести маятника до оси привеса.

Перепишем уравнение иначе

. 10.7)

Это дифференциальное уравнение качаний физического маятника.

Для математического маятника (рис. 10.4) уравнение имеет вид

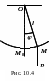
. (10.8)

Сравнивая (10.4) и (10.5), заметим, что они отличаются друг от друга коэффициентами при . Приравняв эти коэффициенты между собой, определим длину соответствующего математического маятника. Период качаний которого равен периоду качаний данного физического маятника

,

откуда

. (10.9)

Таким образом, приведенная длина физического маятника есть длина такого математического маятника, период качаний которого равен периоду качения данного физического маятника.

По формуле Штейнера-Гюйгенса имеем

,

где i _Cx - радиус инерции маятника относительно оси Cx. Тогда

.

Очевидно, что l > d.

Отложим отрезок ОО₁=l. Получим точку О₁, которая называется центром качаний маятника. Ось, проходящая через нее, называется осью качаний маятника.

Обозначим , тогда .

Приведенная длина при оси привеса, проходящей через точку О,

.

Теперь сделаем осью привеса ось О₁ x, тогда приведенная длина маятника

.

Учитывая, что , имеем l₂=d+b.

Следовательно,

. (10.10)

Таким образом, если ось качаний физического маятника сделать осью привеса, то прежняя ось привеса станет его осью качаний (суть теоремы Гюйгенса о взаимности оси привеса и оси качаний физического маятника).

При малых углах (до 15⁰) , тогда (10.7) выглядит

, или , (10.11)

где - частота колебаний маятника.

Решение этого уравнения

=C₁ cos kt+ C₂ sin kt, или =a sin (kt+β), (10.12)

где а – амплитуда колебаний в радианах, β – начальная фаза колебаний. Они, как и произвольные постоянные интегрирования C₁ , C₂ , находятся из начальных условий.

Период малых колебаний физического маятника

.(10.13)

Учитывая (10.9), имеем .