
- •Содержание
- •Глава 1. Постановка транспортных задач 6
- •Глава 2. Определение оптимального плана транспортных задач 28
- •Введение
- •Глава 1.Постановка транспортных задач
- •1.1.Однопродуктовая транспортная модель
- •1.2.Многопродуктовая транспортная модель
- •1.3.Модель производства с запасами
- •1.4. Методы построения опорного плана
- •1.4.1. Метод северо-западного угла
- •1.4.2.Метод минимальной стоимости
- •1.4.3.Метод двойного предпочтения
- •1.4.4.Приближенный метод Фогеля
- •Глава 2.Определение оптимального плана транспортных задач
- •2.1.Решение транспортной задачи методом моди
- •2.2.Дельта-метод решения транспортной задачи
- •2.3.Решение задач закрепления потребителей за поставщиками и клиентуры за автотранспортными предприятиями с учетом дополнительных требований
- •2.3.1.Ограничения в поставках
- •2.3.2.Несбалансированное наличие и потребности
- •2.3.3.Задача закрепления при учете взаимозаменяемости автомобилей
- •2.3.4.Задача на минимизацию времени доставки груза
- •Глава 3.Задача о назначениях
- •3.1.Постановка задачи о назначениях
- •3.2.Венгерский метод решения задачи о назначениях
- •3.3.Применение задачи о назначениях к решению экономических проблем
- •Глава 4.Оптимальное планирование грузооборота
- •4.1.Транспортная сеть и характеристика перевозимых грузов
- •Объёмы потребления грузов
- •Объёмы производства песка
- •4.2.Оптимальное планирование грузоперевозок
- •4.3.Маршрутизация перевозок грузов при помашинных отправках
- •4.4.Составление кольцевых и маятниковых маршрутов
- •Глава 5.Оптимальное планирование работы автобусного парка
- •5.1.Постановка задачи
- •5.2.Двойственная задача линейного программирования
- •5.3. Примеры формулировок двойственных задач
- •5.4. Симметричная и несимметричная двойственные пары. Основы теории двойственности
- •Основная теорема теории двойственности
- •5.5. Условия равновесия в симметричной паре. Экономическая интерпретация
- •5.6.Решение задачи оптимального планирования работы автопарка
- •Глава 6.Область применения сетевых транспортных задач
- •6.1.Примеры применения модели о кратчайшем пути
- •6.2.Алгоритмы нахождения кратчайшего пути
- •6.2.1.Алгоритм для сетей без циклов
- •6.2.2.Алгоритм для сетей с циклами
- •6.2.3.Алгоритм Флойда
- •6.3.Алгоритм нахождения максимального потока в сети
- •6.4.Представление сетевых задач как задач линейного программирования
- •Глава 7.Применение сетевых моделей в транспортировке грузов
- •7.1. Определение кратчайших расстояний между пунктами транспортной сети
- •7.2. Решение задачи коммивояжера методом "ветвей и границ"
- •7.3. Определение развозочных маршрутов для перевозки мелких партий грузов
- •7.3.1. Нахождение кратчайшей связывающей все пункты сети и набор пунктов в маршруты
- •7.3.2. Определение очередности объезда пунктов маршрута
- •Матрица кратчайших расстояний 2-го маршрута
- •7.4. Определение развозочных маршрутов для мелких партий грузов методом Кларка Райта
- •Список литературы
3.3.Применение задачи о назначениях к решению экономических проблем
Пример 3.5: Оптимальное исследование рынка
Группе,
исследующей рынок, требуется получить
данные из n рабочих
мест. В ее распоряжении имеется n
дней, и она предполагает провести по
одному дню в каждом месте, проведя по
aj опросов,
j=![]() .
Вероятность успешного опроса в каждом
месте задается матрицей Р.
Элемент матрицы pij
характеризует вероятность успешного
опроса в течении i-го
дня в j-м
месте,i =
;
j =
.Определить
время проведения опросов, при котором
общее число опросов максимально.
.
Вероятность успешного опроса в каждом
месте задается матрицей Р.
Элемент матрицы pij
характеризует вероятность успешного
опроса в течении i-го
дня в j-м
месте,i =
;
j =
.Определить
время проведения опросов, при котором
общее число опросов максимально.
Сведем данную задачу к задаче о назначениях. Введем величину ri j=pi j aj, показывающую число успешных опросов в j-м месте в течении i-го дня.
![]()
Математическая модель задачи имеет следующий вид :
![]() max.
max.
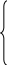
![]() ,
i =
;
,
i =
;
![]() ,
j =
;
xi j
{
0;1 }.
,
j =
;
xi j
{
0;1 }.
Функция R характеризует суммарное число опросов. Его нужно максимизировать. Первое и второе ограничения соответствуют тому, что в течении одного дня можно находиться только в одном месте. Для расчета модели венгерским методом надо перейти к противоположной функции:
![]() ,и
в соответствующей таблице записывать
значения rij
с противоположным
знаком.
,и
в соответствующей таблице записывать
значения rij
с противоположным
знаком.
Пример 3.6: Оптимальное использование торговых агентов
Торговая фирма продает товары
в n
различных городах, покупательная
способность жителей которых оценивается
в bj усл.
ед., j =
![]() .
Для реализации товаров фирма располагает
n
торговыми агентами, каждого из которых
она направляет в один городов.
Профессиональный уровень агентов
различен: доля реализуемых i-м
торговым агентом покупательных
способностей составляет ai,
i =
.
Как следует распределить торговых
агентов по городам, чтобы фирма получила
максимальную выручку от продажи товаров?
.
Для реализации товаров фирма располагает
n
торговыми агентами, каждого из которых
она направляет в один городов.
Профессиональный уровень агентов
различен: доля реализуемых i-м
торговым агентом покупательных
способностей составляет ai,
i =
.
Как следует распределить торговых
агентов по городам, чтобы фирма получила
максимальную выручку от продажи товаров?
Оптимальное решение этой проблемы может быть найдено с помощью задачи о назначениях. В качестве кандидатов выступают торговые агенты, в качестве работ – города. Введем параметр cij=ai∙bj, характеризующий величину покупательных способностей, реализуемых i-м торговым агентом в j-м городе. Управляющие переменные определяют по формуле
![]()
Математическая модель запишется в следующей форме:
![]() max.
max.
 ,
i =
;
,
i =
;
![]() ,
j =
;
,
j =
;
xi j { 0;1 }.
Первое и второе ограничения формализуют соответственно условия о том, что в каждый город направляется один торговый агент, и один торговый агент не может работать в двух городах. Целевая функция С – это сумма реализованных покупательных способностей всеми торговыми агентами во всех городах. Она должна быть максимальна. Для решения задачи венгерским методом надо, как и в предыдущем примере, перейти к противоположной функции.
Глава 4.Оптимальное планирование грузооборота
4.1.Транспортная сеть и характеристика перевозимых грузов
Таблица 64
Объёмы производства грузов
Поставщик (щебень) |
Объёмы производства, т |
А |
140 |
Б |
210 |
Г |
180 |
Н |
210 |
Таблица 65
Объёмы потребления грузов
Потребитель (щебень) |
Объёмы потребления, т |
В |
170 |
И |
180 |
Л |
150 |
Ж |
130 |
3 |
10 |
Таблица 66
