- •664074, Иркутск, ул. Лермонтова, 83
- •1.Основные определения вариационного исчисления
- •2.Необходимые условия экстремума функционала
- •3.Вариационные задачи с подвижными концами
- •4.Ломаные экстремали
- •5.Функционалы, зависящие от нескольких функций
- •6.Задачи с функционалом, содержащим производные высших порядков
- •7.Условный экстремум
- •8.Каноническая форма уравнений эйлера
- •9.Оптимальное управление
- •10.Дифференциальные игры
- •11.Методы решения. Прямые методы
- •12.Методы решения. Метод множителей лагранжа
- •13.Методы решения. Принцип максимума
- •14.Методы решения. Динамическое программирование
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ИРКУТСКИЙ ГОСУДАPСТВЕHHЫЙ
ТЕХНИЧЕСКИЙ УHИВЕPСИТЕТ
 ТЕОРИЯ
ТЕОРИЯ
ОПТИМАЛЬНОГО
УПРАВЛЕНИЯ
Иркутск – 2006 г.
Куцый Н.Н. Теория оптимального управления. - Иркутск, изд-во Иркутск. гос. технич. ун-та, 2006. – 166 с.
Библиогр. 9 назв.
ЛР № 020263 от 30.12.96
Иркутский государственный технический университет
664074, Иркутск, ул. Лермонтова, 83
1.Основные определения вариационного исчисления
Вариационное
исчисление определяет условия, при
которых функционалы достигают своего
экстремума. Функционал определяется
следующим образом. На множестве
![]() функций задан функционал, если каждой
функции
функций задан функционал, если каждой
функции
![]() ,
принадлежащей
,
,
принадлежащей
,
![]() ,
соответствует определенное число.
Функционал можно рассматривать как
функцию, в которой роль независимых
переменных играют другие функции )одна
или несколько). Приведём несколько
примеров функционала.
,
соответствует определенное число.
Функционал можно рассматривать как
функцию, в которой роль независимых
переменных играют другие функции )одна
или несколько). Приведём несколько
примеров функционала.
Длина
линии
![]() ,
,
![]() ,
,
![]() ,
где
,
где
![]() множество
функций
множество
функций
![]() ,
определенных на отрезке
,
определенных на отрезке
![]() и обладающих на нём непрерывной
производной есть функционал
и обладающих на нём непрерывной
производной есть функционал
![]() .
.
Пусть
![]() ,
пройденный транспортным средством за
время
,
пройденный транспортным средством за
время
![]() ,
является функционалом скорости
,
является функционалом скорости
![]() транспортного средства
транспортного средства
![]() .
.
Время
перемещения из одного положения
![]() в другое
в другое
![]() точки в плоскости
точки в плоскости
![]() ,
где для каждой пары значений координат
скорость точки
,
где для каждой пары значений координат
скорость точки
![]() задана и не зависит от направления
движения, определяется функционалом
вида
задана и не зависит от направления
движения, определяется функционалом
вида
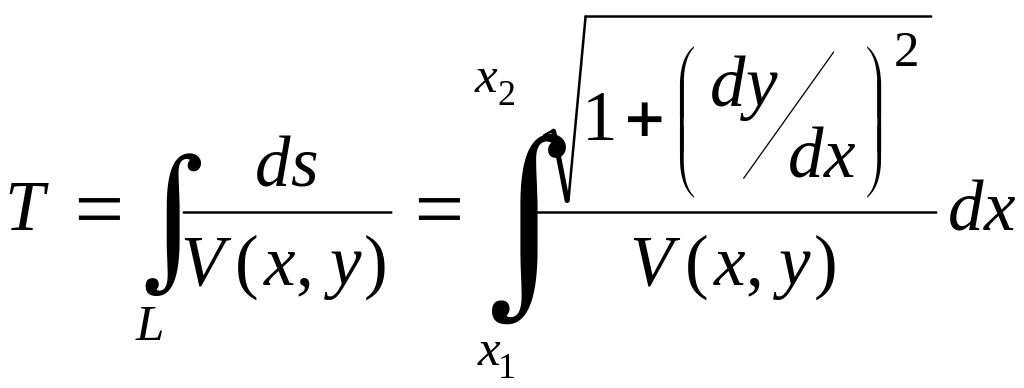 ,
,
где
![]() .
.
Примером функционала более общего вида может служить выражение
![]() .
.
Здесь
![]() независимая
переменная;
независимая
переменная;
![]() искомая
функция
искомая
функция
![]() ;
;
![]() производная
производная
![]() .
.
В задачах вариационного исчисления
необходимо указывать, в каком классе
функций ищется экстремум функционала.
Рассмотрим следующие классы функций.
задачах вариационного исчисления
необходимо указывать, в каком классе
функций ищется экстремум функционала.
Рассмотрим следующие классы функций.
Н
 епрерывные
функции не имеют разрывов. Например,
функция, изображенная на рис. 1.1, непрерывна
на отрезке
,
а функция на рис. 1.2 имеет разрывы. Гладкие
функции являются не только непрерывными,
но имеют и непрерывную первую производную.
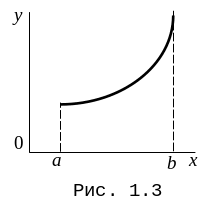
Гладкая функция приведена на рис. 1.3.
Решение технических задач методами
вариационного исчисления часто приводит
к необходимости поиска экстремума
функционала в классах кусочно-непрерывных
или кусочно-гладких функций.
Кусочно-непрерывная функция, которая
имеет разрывы в виде скачков представлена
на рис. 1.4. Кусочно-гладкая функция (рис.
1.1) имеет изломы в отдельных точках.
епрерывные
функции не имеют разрывов. Например,
функция, изображенная на рис. 1.1, непрерывна
на отрезке
,
а функция на рис. 1.2 имеет разрывы. Гладкие
функции являются не только непрерывными,
но имеют и непрерывную первую производную.
Гладкая функция приведена на рис. 1.3.
Решение технических задач методами
вариационного исчисления часто приводит
к необходимости поиска экстремума
функционала в классах кусочно-непрерывных
или кусочно-гладких функций.
Кусочно-непрерывная функция, которая
имеет разрывы в виде скачков представлена
на рис. 1.4. Кусочно-гладкая функция (рис.
1.1) имеет изломы в отдельных точках.
Р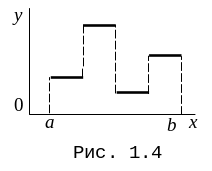 ассмотрим
классификацию экстремумов функционала.
С этой целью введём понятие функций
сравнений. если функционал
ассмотрим
классификацию экстремумов функционала.
С этой целью введём понятие функций
сравнений. если функционал
![]() исследуется на экстремум и имеется
некоторая функция
исследуется на экстремум и имеется
некоторая функция
![]() ,
которая подозревается в качестве
функции, доставляющей экстремум
функционалу, то значение функционала
,
которая подозревается в качестве
функции, доставляющей экстремум
функционалу, то значение функционала
![]() сопоставляется с его значениями на
некотором множестве функций
,
которые называются функциями сравнения.
Множеству функций сравнения принадлежит
также и исследуемая функция
.
На множестве функций сравнения существует
положительная (отрицательная) разность
сопоставляется с его значениями на
некотором множестве функций
,
которые называются функциями сравнения.
Множеству функций сравнения принадлежит
также и исследуемая функция
.
На множестве функций сравнения существует
положительная (отрицательная) разность
![]() ,
,
если имеет место минимум (максимум_ функционала при .
Окрестностью
нулевого порядка или сильной окрестностью
называется множество непрерывных
функций сравнения
таких, что при некотором положительном
числе
![]() имеет место неравенство
имеет место неравенство
![]() ,
,
![]() .
.
Окрестностью первого порядка или слабой окрестностью называется множество кусочно-гладких функций сравнения таких, что при некотором положительном числе имеет место
![]() ,
.
,
.
Минимум функционала , который достигается на в её сильной (слабой) окрестности, называется сильным (слабым) минимумом функционала . Аналогично максимум функционала , который достигается на в её сильной (слабой) окрестности, называется сильным (слабым) максимумом функционала . Сильный и слабый экстремумы являются относительными экстремумами. Абсолютным экстремумом функционала называется экстремум функционала, который найден по всей совокупности функций, на которых значение функционала определено. Абсолютный экстремум функционала является в то же время относительным.
П онятия
абсолютного и относительно экстремума
функционала можно проиллюстрировать
следующим примером. Требуется найти
кратчайший путь между пунктами
онятия
абсолютного и относительно экстремума
функционала можно проиллюстрировать
следующим примером. Требуется найти
кратчайший путь между пунктами
![]() и
и
![]() (рис. 1.5), разделенным непроходимым
препятствием (озеро, гора, лесной массив
и т. п.). Имеется множество путей, огибающих
препятствие слева (справа), есть кратчайший
путь. Допустим, что путь справа короче
пути слева. В этом случае абсолютный
минимум функционала, в качестве которого
выбрано расстояние между пунктами,
достигается на кратчайшем пути, огибающем
препятствие справа. Относительный
минимум достигается на кратчайшем пути,
огибающем препятствие слева, так как
этот путь короче других путей, огибающих
препятствие слева.
(рис. 1.5), разделенным непроходимым
препятствием (озеро, гора, лесной массив
и т. п.). Имеется множество путей, огибающих
препятствие слева (справа), есть кратчайший
путь. Допустим, что путь справа короче
пути слева. В этом случае абсолютный
минимум функционала, в качестве которого
выбрано расстояние между пунктами,
достигается на кратчайшем пути, огибающем
препятствие справа. Относительный
минимум достигается на кратчайшем пути,
огибающем препятствие слева, так как
этот путь короче других путей, огибающих
препятствие слева.
Понятие
сильного и слабого экстремума удобно
пояснить следующим примером. Рассмотрим
ситуацию, в которой парусно-весельная
лодка движется по озеру навстречу ветру
из пункта
в пункт
.
Предполагается, что скорость движения
под парусами выше скорости движения на
вёслах, но прямо против ветра двигаться
под парусами невозможно. В этом примере
на прямой
![]() достигается сильный минимум функционала,
в качестве которого выбрано время
перемещения лодки из пункта
в
.
Любая траектория движения лодки на
вёслах лежит в окрестности первого
порядка (например, штриховая линия на
рис. 1. 6) увеличивает время пути, хотя
расстояние первог
достигается сильный минимум функционала,
в качестве которого выбрано время
перемещения лодки из пункта
в
.
Любая траектория движения лодки на
вёслах лежит в окрестности первого
порядка (например, штриховая линия на
рис. 1. 6) увеличивает время пути, хотя
расстояние первог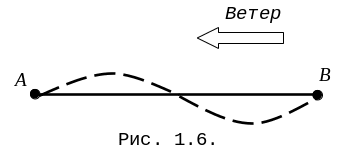 о
порядка от прямой
мало. Время движения между пунктами
и
можно сократить по сравнению с движением
лодки по прямой
,
если двигаться под парусами, короткими
галсами (рис. 1.7) в окрестности нулевого
порядка от прямой
.
таким образом, на прямой
в рассматриваемом примере сильный
минимум функционала не достигается.
Отметим, что всякий сильный экстремум
функционала является в то время и слабым
функционалом, так как для сильного
экстремума сравнение выполняется с
кривыми, которые находятся в близости
нулевого порядка, а для слабого сравнение
производится с ещё более узким классом
кривых, которые находятся в окрестности
первого порядка от исследуемой функции.
о
порядка от прямой
мало. Время движения между пунктами
и
можно сократить по сравнению с движением
лодки по прямой
,
если двигаться под парусами, короткими
галсами (рис. 1.7) в окрестности нулевого
порядка от прямой
.
таким образом, на прямой
в рассматриваемом примере сильный
минимум функционала не достигается.
Отметим, что всякий сильный экстремум
функционала является в то время и слабым
функционалом, так как для сильного
экстремума сравнение выполняется с
кривыми, которые находятся в близости
нулевого порядка, а для слабого сравнение
производится с ещё более узким классом
кривых, которые находятся в окрестности
первого порядка от исследуемой функции.