
- •664074, Иркутск, ул. Лермонтова, 83
- •1.Основные определения вариационного исчисления
- •2.Необходимые условия экстремума функционала
- •3.Вариационные задачи с подвижными концами
- •4.Ломаные экстремали
- •5.Функционалы, зависящие от нескольких функций
- •6.Задачи с функционалом, содержащим производные высших порядков
- •7.Условный экстремум
- •8.Каноническая форма уравнений эйлера
- •9.Оптимальное управление
- •10.Дифференциальные игры
- •11.Методы решения. Прямые методы
- •12.Методы решения. Метод множителей лагранжа
- •13.Методы решения. Принцип максимума
- •14.Методы решения. Динамическое программирование
5.Функционалы, зависящие от нескольких функций
В
отличие от простейших задач вариационного
исчисления рассмотрим общее выражение
для функционала, зависящего от
![]() функций
функций
![]()

![]() ,
,
где
![]() и
и
![]() граничные
условия, заданные в виде чисел;
граничные
условия, заданные в виде чисел;
![]() непрерывная
подынтегральная функция, обладающая
непрерывными частными производными до
третьего порядка включительно по всем
аргументам.
непрерывная
подынтегральная функция, обладающая
непрерывными частными производными до
третьего порядка включительно по всем
аргументам.
Вариационная
задача состоит в определении условий,
которым удовлетворяет вектор-функция
![]() ,
доставляющая функционалу (5.1) экстремум
при граничных условиях (5.2).
,
доставляющая функционалу (5.1) экстремум
при граничных условиях (5.2).
Необходимые
условия экстремума для функционала
(5.1) можно получить следующим образом.
Предположим, что экстремум существует
и достигается на функциях
![]() .
Если зафиксировать все функции, кроме
одной
.
Если зафиксировать все функции, кроме
одной
![]() ,
которой будем придавать приращение, то
вариация функционала (5.1) будет зависеть
только от одной функции и из условия
,
которой будем придавать приращение, то
вариация функционала (5.1) будет зависеть
только от одной функции и из условия
![]() следует уравнение Эйлера для функции
следует уравнение Эйлера для функции
![]()
![]() .
.
Аналогичные рассуждения относительно любой неизвестной функции позволяют получить необходимые условия экстремума функционала (5.1) в виде системы уравнения Эйлера
![]()
Второе необходимое условие экстремума – условие Лежандра – устанавливается, как в простейшей вариационной задаче, на основе неотрицательности (в случае минимума функционала) или неположительности (в случае максимума функционала) второй вариации функционала, зависящего от нескольких функций. Из этого условия вытекает необходимое условие Лежандра - неотрицательность (неположительность) квадратичной формы
![]()
в каждой точке экстремали в случае минимума (максимума) функционала (5.1).
Условия Лежандра в том случае, когда на экстремали достигается минимум функционала, можно записать в виде неравенств, выполнение которых обеспечивает неотрицательность формы (5.4)

Необходимые условия минимума функционала (5.1) в форме (5.5) называются условиями Лежандра-Клебша. В случае поиска максимума функционала знаки неравенств (5.5) меняются на обратные.
Условия
трансверсальности для вариационных
задач с подвижными концами и функционалом,
зависящим от нескольких функций,
выводятся из рассмотрения дифференциала
функционала (5.1), который для случая,
когда
![]() экстремаль,
имеет вид
экстремаль,
имеет вид
![]() .
.
На концах экстремали должны выполняться условия трансверсальности
![]() .
.
В
том случае, когда конец
![]() фиксирован, а второй конец расположен
на гиперповерхности
фиксирован, а второй конец расположен
на гиперповерхности
![]() ,
условия трансверсальности (5.6) означают,
что вектор
,
условия трансверсальности (5.6) означают,
что вектор
![]()
ортогонален
вектору
![]() и, следовательно, коллинеарен градиенту
функции
и, следовательно, коллинеарен градиенту
функции
![]() .
В этом случае условия трансверсальности
можно записать в виде
.
В этом случае условия трансверсальности
можно записать в виде
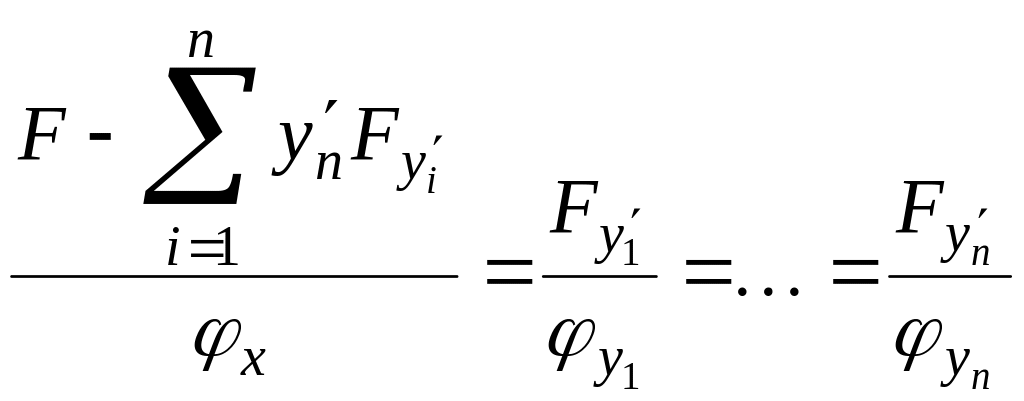 .
.
В качестве примера на экстремум рассмотрим вариационную задачу с функционалом

с граничными условиями
![]() ,
,
![]() .
.
Система дифференциальных уравнений Эйлера (5.3), т.е.
![]()
в данном примере имеет вид
![]() ,
,
![]() .
.
Исключая
одну из неизвестных функций, например
![]() ,
получаем
,
получаем
![]() .
.
Интегрируя линейное дифференциальное уравнение (5.8) с постоянными коэффициентами, имеем
![]() ,
,
![]() .
.
Используя
граничные условия, находим
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
следовательно, экстремалями функционала
(5.7) является
,
следовательно, экстремалями функционала
(5.7) является
![]() ,
,
![]() .
.
