8.Каноническая форма уравнений эйлера
Уравнения Эйлера
для функционала вида
можно записать в канонической или гамильтоновой форме.
Если
матрица
неособенная, то из уравнений
можно
выразить
через
:
.
Гамильтонианом
для функционала (8.2) называется функция
от
:
,
где определяется выражением (8.4).
Дифференцированием гамильтониана получаем следующие соотношения:
С
учётом соотношения (8.1), (8.2) и (8.3) выражение
(8.6) принимает вид канонической или
гамильтоновой системы уравнений Эйлера,
в которой переменные
называются каноническими:
Пользуясь определением гамильтониана согласно (8.5), выражение для дифференциала функционала (8.2) можно записать в виде
.
Условия трансверсальности (5.6), т.е.
,
на концах экстремали с учётом определения гамильтониана имеют вид
.
Каноническую систему (8.7) можно рассматривать как систему уравнений Эйлера для функционала
.
Выражение (8.8) для дифференциала можно записать в виде системы уравнений
Исключая
в системе (8.9), получаем уравнение в
частных производных первого порядка,
которое называется уравнение
Гамильтона-Якоби:
.
Полным интегралом уравнения (8.10) в частных производных первого порядка называется его решение, содержащее столько произвольных постоянных, каково число независимых переменных.
Учитывая,
что уравнение (8.10) не содержит неизвестной
функции, а содержит только её частные
производные, полный интеграл можно
взять в виде
,
где
произвольные
постоянные.
Предполагается,
что
непрерывно дифференцируема по параметрам
и каждая частная производная
непрерывно дифференцируема по всем
аргументам.
При
дополнительном предположении о том,
что определитель
,
имеет место теорема Якоби.
Если известен полный интеграл уравнения Гамильтона-Якоби, то равенства
,
,
где
произвольные
постоянные, дают решение канонической
системы (8.7), т.е.
которое
зависит от
произвольных постоянных.
В качестве примера найдём экстремали функционала
.
Гамильтониан
,
следовательно
или
Решение можно искать в виде
.
Подстановка решения (8.12) в уравнение Гамильтона-Якоби (8.11) данного примера даёт
,
,
.
Полагая
,
,
получаем решение в виде
.
Общий интеграл уравнения Эйлера-Лагранжа в силу теоремы Якоби
или
.
9.Оптимальное управление
Задачи оптимизации связанные с оптимальным управлением процессами или объектами различной физической природы (например, электрической, механической, химической и т.п.), являются весьма важными для приложения в различных областях техники и промышленности.
Состояние
физического процесса или объекта
характеризуется переменными состояния
(фазовыми координатами)
.
Физический процесс или динамика объекта
описывается системой дифференциальных
уравнений (уравнениями состояния),
например:
где
переменные
управления;
время.
Переменными
состояния в электротехнике обычно
являются электрические токи и напряжения,
в механике – координаты, скорости и
ускорения, в химии – концентрации
веществ. Свободные переменные
позволяют ставить задачу оптимального
управления, т.е. наилучшем (оптимальном)
в смысле заданного критерия выборе
переменных управления.
Задача
оптимального управления заключается
в определении переменных управления
в интервале
,
которые обеспечивают экстремум (максимум
или минимум) критерия качества, заданного
в виде функционала
,
и удовлетворяют ограничениям, например
,
определяющим
замкнутую область допустимых управлений
.
Примерами критериев качества являются
энергетические затраты, время достижения
цели, ошибка управления, стоимость и
т.п.
Оптимальное
управление
определяет оптимальную траекторию
в
мерном
фазовом пространстве, движение по
которой из начального состояния в
конечное обеспечивает достижение
оптимального значения функционала
(критерия качества.
Решение
задачи оптимального управления требует
задания начальных
и конечных
состояний. Во многих задачах управления
начальное состояние
задаётся в виде
мерного
многообразия начальных состояний
(гиперповерхность, линия или точка в
пространстве состояний)
.
Таким
же образом может быть задано конечное
значение
в виде
мерного
многообразия конечных состояний
.
Ряд задач оптимального управления может быть сведён к рассмотренной задаче. Например, задача оптимального управления с функционалом вида
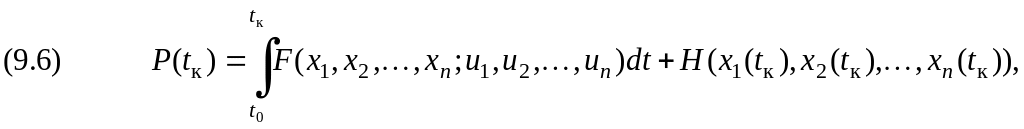
где
функция
конечного состояния, приводится к
задачам с функционалом (9.2.), т.е.
,
следующим образом:
,
где
.
Нестационарные
(неавтономные) задачи (системы), когда
одна или несколько заданных функций
и
явно зависят от времени
(независимой переменной), сводится к
рассмотренной задаче путём введения
новой переменной состояния
,
где
,
,
.
В задачах оптимального управления, в которых ограничения (9.3), т.е.
,
на
переменные управления
явно зависят от переменных состояния
(с учётом и зависимости от
),
методом введения новых переменных
управления эту зависимость можно
исключить. Например, ограничение вида
путём
введения новой переменной управления
таким образом, что
,
приводится к
.
Задачу
оптимального управления можно
рассматривать как вариационную задачу
на условный экстремум, например как
задачу Лагранжа, Майера или Больца.
Однако применение вариационных методов
к задачам оптимального управления
встречает определенные трудности, так
как задачи оптимального управления
встречает определенные трудности, так
как задачи оптимального управления
содержат ряд особенностей, не учитываемых
в вариационных задачах. Задачи оптимального
управления по сравнению с вариационными
задачами на условный экстремум имеют
следующие особенности. Во-первых,
значения управления
,
которое рассматривается как одна из
неизвестных функций, принадлежат
замкнутому множеству
,
например, вектор управления может быть
ограничен условием
.
Во-вторых, подынтегральное выражение
функционала и уравнения движения,
которые рассматриваются как уравнения
связи, не зависят от производной
управления
,
что приводит к вырожденному виду одного
из уравнений Эйлера, которое в этом
случае не будет дифференциальным.
В-третьих, в вариационных задачах
необходимые условия минимума функционала
выведены в предположении, что неизвестные
функции принадлежат классу дважды
дифференцируемых функций, а в задаче
оптимального управления рассматривается
более широкий класс кусочно-непрерывных
функций. В задачах оптимального управления
экстремум функционала часто достигается
на управлении
,
которое имеет точки разрыва первого
рода, что в силу уравнений движения
приводит к наличию точек разрыва
производной оптимальной траектории, а
положение и число точек разрыва заранее
неизвестны.
Оптимальное управление может рассматриваться как обобщенное вариационное исчисление. Все задачи вариационного исчисления, связанные с максимизацией или минимизацией интегралов
при соответствующих ограничениях и граничных условиях, могут быть сформулированы как задачи оптимального управления, если произвести замену
Подстановка соотношений (9.13) в функционал (9.12) сводит задачу вариационного исчисления к задаче оптимального управления с функционалом
где
.
Следует отметить, что в задачах оптимального управления обычно на переменные управления наложены ограничения (9.3), т.е.
,
которые вызывают определенные затруднения в случае применения методов классического вариационного исчисления. Это стимулировало разработку специальных методов для решения задач оптимального управления, таких, как принцип максимума Понтрягина и динамическое программирование Беллмана.
Рассмотрим
пример постановки задачи оптимального
управления. Кораблю предстоит проплыть
через область сильных течений. Величина
и направления скорости течения задаются,
как функции фазовых переменных
,
,
где
прямоугольные
координаты,
компоненты
вектора скорости течения в направлении
осей
и
соответственно (рис. 9.1). Величина скорости
корабля относительна постоянна и равна
.
Уравнения движения корабля имеют вид
где
угол
курса, т.е. угол между осью корабля и
фиксированной координатной осью
;
координаты
корабля.
На
рис. 9.1
масштабная
постоянная, стрелками указаны направления
оси корабля, т.е. угол курса
который в данной задаче является
управляющей функцией.
Задача оптимального управления заключается в выборе такого угла курса, при котором корабль за минимальное время пройдет путь от точки до точки .
Если
составляющие скорости течения
и
постоянны, то оптимальной траекторией
движения с минимальным временем будет
прямая линия.