2.Необходимые условия экстремума функционала

Рассмотрим простейшую задачу вариационного исчисления. Требуется найти минимум функционала

среди кусочно-гладких линий, которые соединяют точки и , т.е. .

Обычно предполагается непрерывность подынтегральной функции по совокупности её аргументов, а также существование и непрерывность всех её частных производных до третьего порядка включительно.

Определим условия, которым должна удовлетворять функция , которая доставляет слабый относительный минимум функционалу (2.10). Необходимые условия слабого минимума будут тем более необходимыми условиями сильного и абсолютного минимумов.

И зменим вид функции путём прибавки к ней произвольной кусочно-гладкой функции, помноженной на малый параметр , т.е. получим уравнение варьируемой кривой (рис. 2.1) в виде

.

Если произвольная кусочно-гладкая функция удовлетворяет условиям , то однопараметрическое семейство функций (2.2) при достаточно малых значениях параметра принадлежит некоторой окрестности первого порядка функции .

Функционал на семействе функций является функцией параметра :

.

Дифференцируя дважды функционал (3.3) по параметру , имеем

,

,

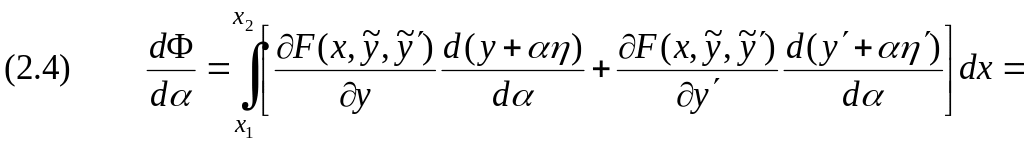
где введены обозначения частных производных:

Первой вариацией функционала называется производная от

по параметру в точке , т.е.

.

Второй вариацией функционала называется вторая производная (2.5) от

по параметру в точке , т.е.

.

Необходимым условием экстремума функционала является равенство нулю его первой вариации (2.6). В случае минимума функционала его вторая производная (2.7) должна быть неотрицательной: , а в случае максимума – неположительной: .

С целью получения необходимого условия экстремума функционала в форме уравнения Эйлера первую вариацию функционала приравняем нулю при . Тогда выражение (2.4) примет вид

Интегрируем по частям второй член выражения (2.8):

Учитывая, что произвольная функция в точках и обращается в нуль, т.е. , выражение (2.9) запишем в виде

Необходимое условие экстремума функционала (2.8) с учётом соотношения (2.10) получим в форме

К этому выражению применим лемму Лагранжа, согласно которой, если непрерывная функция обладает тем свойством, что

для любой гладкой функции , то обязательно имеет место для всех .

На основании леммы Лагранжа необходимое условие экстремума функционала (2.11) можно записать в форме уравнения Эйлера

Гладкое решение уравнения Эйлера называется экстремалью.

Уравнение (2.12) можно представить в другой форме. Выполним полное дифференцирование по второго члена уравнения Эйлера

.

Подстановка (2.13) в (2.12) даёт уравнение Эйлера в виде нелинейного дифференциального уравнения второго порядка

.

В общем случае решение уравнения Эйлера вызывает определенные трудности. Кроме того, экстремали в некоторых случаях могут не доставлять ни максимума, ни минимума функционалу, так как уравнение Эйлера является только необходимым условием экстремума. Если уравнение не выполняется ни для одной функции, то это значит, что для данного функционала не существует экстремума в классе кусочно-гладких функций.

Кроме уравнения Эйлера имеется второе необходимое условие экстремума функционала – условие Лежандра, которое позволяет различать максимум и минимум функционала. Условие Лежандра выводится из рассмотрения второй вариации функционала (2.5).

Интегрируя по частям второй член в выражении (2.5), получаем

,

так как . С учётом соотношения (2.15) выражение (2.5) принимает вид

.

Выберем произвольную функцию , достаточно малую по абсолютной величине, но быстро изменяющуюся по . В этом случае знак второй вариации совпадает со знаком , так как мало, а довольно велико.

Ранее указывалось, что в случае минимума функционала вторая вариация (2.16) должна быть неотрицательной: , а в случае максимума – неположительной: .

Итак, второе необходимое условие экстремума – условие Лежандра – формулируется следующим образом. Для того чтобы функция доставляла минимум функционалу

,

должно выполняться неравенство , а в случае максимума функционала – неравенство . В точках экстремали, в которых , возможны изломы. Случай вырожденного функционала имеет место, если равно нулю тождественно.

В качестве примера применения необходимых условий исследуем функционал

при граничных условиях , .

Для функционала (2.17) определяем производные , . В заданном интервале , следовательно, на экстремалях может достигаться минимум функционала.

Уравнение Эйлера в данном примере имеет вид

.

Общее решение уравнения (2.18) можно записать в форме

.

Из граничных условий получим два уравнения для определения и :

Решение системы (2.19) даёт , . Тогда уравнение экстремали имеет вид

.

Рассмотрим третье необходимое условие экстремума функционала – условие Вейерштрасса. Если линия доставляет сильный минимум (максимум) функционалу (2.1), т.е.

,

то функция Вейерштрасса

при произвольных конечных значениях во всех точках экстремали неотрицательна (неположительна).

Отметим, что необходимое условие слабого минимума является в то же время необходимым условием сильного минимума, но не обратно.

В качестве четвертого необходимого условия экстремума функционала рассмотрим условие Якоби. Если линия доставляет сильный минимум (максимум) функционалу (2.1), т.е.

,

вторая вариация (2.5), т.е.

,

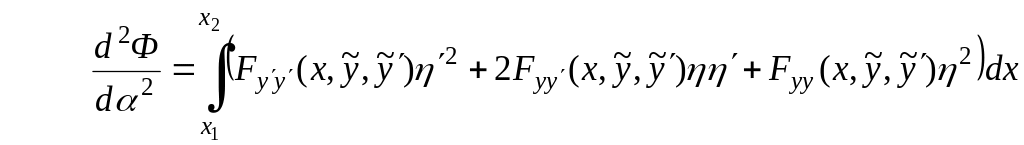в точке должна быть неотрицательной:

,

.

Функции , для которых и выполняются условия (2.21), доставляют минимум функционалу (2.20). Уравнение Эйлера для функционала

называется уравнением Якоби.

При выполнении условия Лежандра

,

из условий

следует, что . Точки и на экстремали называются сопряженными, если

,

причём , .

Условие Якоби заключается в следующем. Если экстремаль , доставляет минимум функционалу (2.1), т.е.

,

то она не содержит точек, сопряженных точке .