7.Условный экстремум

Ранее рассматривались вариационные задачи, в которых на функцию , которая даёт экстремум функционалу, не наложены какие-либо дополнительные условия. Экстремум в этом случае называют безусловным.

Существует также ряд вариационных задач на условный экстремум. В этих вариационных задачах функции, которые доставляют экстремум функционалу, подчинены добавочным условиям.

Простейшим примером вариационной задачи на условный экстремум может служить задача о нахождении кратчайшего расстояния между двумя точками, в которой требуется найти минимум функционала

при условии, что кривая, которая соединяет эти точки, лежит на некоторой поверхности, например на сфере

.

Другим примером является задача, в которой среди всех линий заданной длины требуется найти такую, которая ограничивала бы наибольшую площадь. Вариационные задачи этого типа называют изопериметрическими.

В общем случае изопериметрическая задача формулируется следующим образом. Среди всех кусочно-гладких вектор-функций , которые принимают заданные значения на концах интервала , найти функцию, доставляющую экстремум функционалу

,

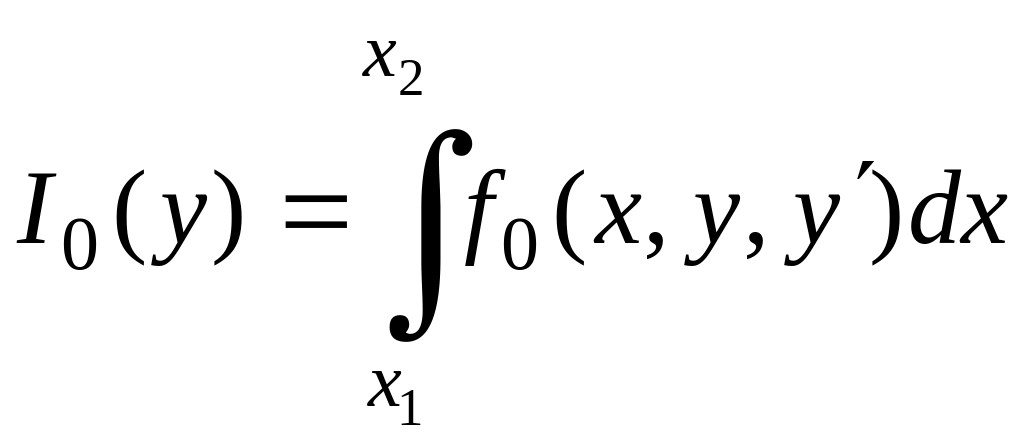при связях

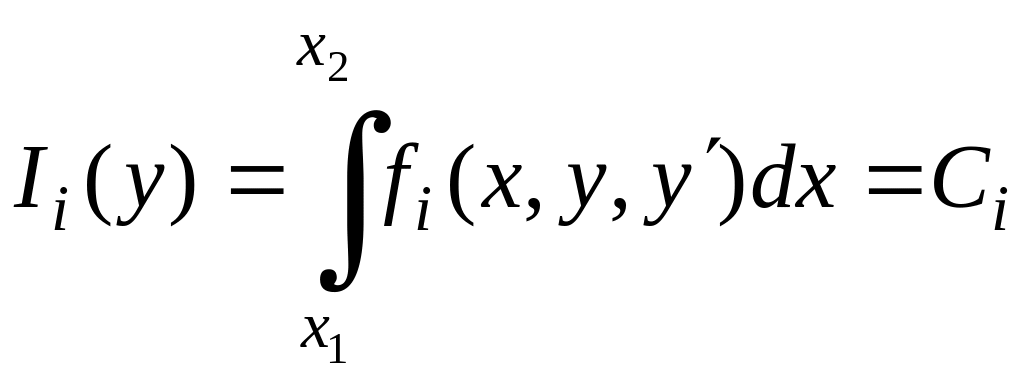
где константы.

Функции , определены и имеют непрерывные по совокупности всех своих аргументов производные второго порядка, когда точка , принадлежит некоторой области пространства , а вектор пробегает любые конечные значений. Вариации функционалов , взятые на минимизирующем векторе, линейно независимы.

Кроме изопериметрической задачи, к вариационным задачам на условный экстремум относятся задачи Лагранжа, Майера и Больца. Общая задача Лагранжа формулируется следующим образом. Среди всех кусочно-гладких вектор-функций , доставляющую экстремум функционалу

при связях

и условиях на концах

,

где функции определены и имеют непрерывные по совокупности всех своих аргументов частные производные третьего порядка. Матрица имеет ранг во всех точках , принадлежащих некоторой области пространства , когда вектор пробегает любые значений на концах. Матрица имеет ранг . Функции обладают непрерывными частными производными третьего порядка. Связь называется голономной, если она не содержит производных или может быть приведена к виду, не содержащему производных. Неголономные связи содержат как сами неизвестные функции , так и их производные .

Примером задачи Лагранжа может служить задача Чаплыгина, в которой требуется найти, по какой замкнутой кривой в горизонтальной плоскости должен двигаться центр тяжести самолёта, имеющего собственную скорость , чтобы за время облететь наибольшую площадь, если дано постоянное направление и постоянная величина скорости ветра . Если ось совместить с направлением скорости ветра, обозначить через угол между направлением оси самолёта и осью , и принять за координаты цента тяжести самолёта, то задача Чаплыгина водится к задаче Лагранжа по нахождению функционала

при неголономных связях

,

.

Вариационная задача на условный экстремум в форме задачи Майера ставится следующим образом. Среди систем гладких функций , удовлетворяющих связям

и условиях на концах

,

,

найти такую систему функций, в которой имеет при экстремум.

Задача Майера в форме задачи с подвижными концами может ставиться так. Среди систем гладких функций , которые удовлетворяют связям и условиям на концах

,

,

найти систему функций, в которой имеет максимум на правом конце.

В качестве примера задачи Майера рассмотрим движение ракеты в вертикальной плоскости. Если пренебречь силой сопротивления воздуха и рассматривать ракету как материальную точку с единичной массой, на которую действует сила тяжести и реактивная сила , постоянная по величине, но с переменным углом наклона , то уравнения движения ракеты имеют вид

,

,

где земное ускорение.

Задача о нахождении пути, вдоль которого на полёт затрачивается наименьшее время при соответствующих начальных и конечных условиях, состоит в отыскании среди всех функций , , , функции, которая минимизирует время полёта и которая удовлетворяет дифференциальным связям (7.1).

Заменив на , дифференциальные связи (7.1) можно записать в виде

Задача Майера в этом случае формулируется в нормальной форме. Требуется найти такую систему функций , при которой время полёта было наименьшим, выполнялись дифференциальные связи (7.2) и условия на концах , , .

Задача Больца заключается в нахождении среди всех кусочно-гладких вектор-функций функции, которая доставляет экстремум функционалу

при связях

и условиях на концах

.

Предполагается, что функции и имеют непрерывные частные производные третьего порядка по совокупности всех своих аргументов в некоторой открытой области мерного пространства. Матрица имеет ранг во всех точках указанной выше области. Функции и обладают непрерывными частными производными по совокупности всех своих аргументов в мерной области пространства точек Ю а матрица имеет ранг во всех точках указанной области.

Как и в задачах Лагранжа и Майера, в задаче Больца должно выполняться так называемое условие некасания, т.е. рассматриваются такие вектор-функции сравнения , для которых ранг матрицы

равным двум.

Задача Больца эквивалентна задаче Лагранжа, в которой среди всех кусочно-гладких вектор-функций отыскивается вектор-функция, которая доставляет экстремум функционалу

при связях , и условиях на концах , .

К задаче Лагранжа могут быть сведены задача Майера и изопериметрическая задача. Если в изопериметрической задаче ввести функции

,

то изопериметрическая задача превращается в задачу Лагранжа поиска экстремума функционала

при дифференциальных связях , условиях на концах , и условиях на исходной изопериметрической задачи. Следует отметить, что изопериметрическая задача является частным случаем задачи Больца.

Задача Майера приводится к задаче Лагранжа, в которой среди всех кусочно-гладких вектор-функций отыскивается вектор-функция, доставляющая экстремум функционалу

при связях , , , , , , , .

Необходимо отметить, что изопериметрическая задача, задача Лагранжа и задача Майера могут рассматриваться как частные случаи задачи Больца, хотя задачи Лагранжа, Майера и Больца обладают степенью общности.