3.Вариационные задачи с подвижными концами
В
вариационных задачах с подвижными
концами рассматривается функционал,
который зависит от линий
:
,
г
де
линия
перемещается так, что её концы движутся
вдоль двух заданных линий
и
(рис. 3.1). Требуется найти среди линий
такую линию, которая доставляет экстремум
функционалу (3.1). В отношении подынтегральной
функции предполагается её непрерывность
по совокупности аргументов, а также
существование и непрерывность её частных
производных до третьего порядка
включительно.
В такой постановке задачи общее уравнение Эйлера, которое является нелинейным дифференциальным уравнением второго порядка, зависит от двух произвольных постоянных, определяемых из условий трансверсальности.
Определим
условия трансверсальности. С этой целью
зададим перемещение линии
с помощью параметра
так, что однопараметрическое семейство
линий
относит каждому значению параметра
одно из возможных положений линии
.
Если параметр
будет определять положение точки на
линии
,
то абсцисса этой точки и параметр
являются функциями
.
В этом случае линии
и
заданы соответственно параметрическими
уравнениями
,
,
,
,
.
На семействе линий функционал превращается в функцию
.
Дифференцируя по соотношение (3.2), имеем
.
Подынтегральное выражение в соотношении (3.3) с учётом уравнения Эйлера (2.12), т.е.
можно представить в виде
.
Подстановка (3.4) в выражение (3.3) даёт соотношение
.
Выражение (3.5) преобразуем с учётом соотношения
или
.
Тогда подстановка (3.6) в выражение (3.5) даёт
Если линия доставляет экстремум функционалу (3.1), т.е.
,
то
при
любых
и
.
Выбрав
при
или
при
и учтя соотношение (3.7), т.е.
,
из условия экстремума функционала (3.8) , т.е.
,
получим следующие условия трансверсальности:
Эти условия позволяют определить положение концов экстремали путём вычисления двух произвольных постоянных, от которых зависит общее решение уравнения Эйлера, так как оно является дифференциальным уравнением второго порядка.
Если
заданы уравнения
линии
и
линии
,
то с учётом соотношений
и
условия трансверсальности (3.9) примут
вид
Если
линия
задана уравнением
,
а линия
- уравнением
,
то (3.9) получим в форме
,
.
В
случае, когда на перемещение концов
экстремали не наложены ограничения, на
обоих концах экстремали выполняются
условия
,
.
Рассмотрим теперь в задаче с подвижными концами вариации функционала, происходящие как от вариации искомой функции, так и от вариации концов.
На
рис. 3.2 изображены исходная функция
и функция
,
к которой добавлена вариация
.
Приращение функционала при переходе
от
к
имеет вид
.
В
ыделим
главную, линейную, часть приращения
функционала, его первую вариацию
.
После того как второй член подынтегрального выражения проинтегрируем по частям, первая вариация функционала примет вид
.
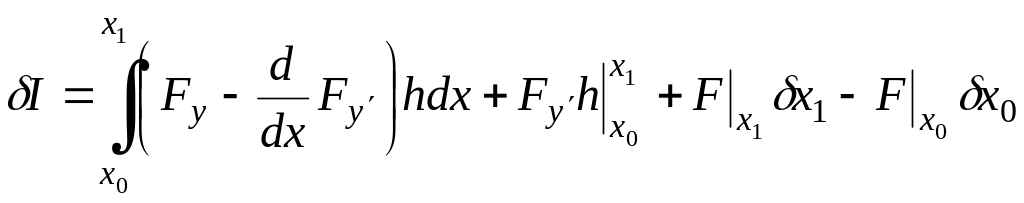Так
как с точностью до бесконечно малых
высшего порядка
и
,
то вариацию функционала можно записать
в виде
.
Выражение (3.10) для вариации функционала состоит из интегрального члена, происходящего от вариации внутри исходного промежутка интегрирования, и членов от вариации его концов.
Из
рассмотрения (3.10) также могут быть
получены условия трансверсальности в
задаче с подвижными концами. Пусть
необходимо найти экстремум функционала
среди кривых
концы которых перемещаются по линиям
и
.
Примером такой задачи может служить
задача о нахождении кратчайшего
расстояния, например, между двумя
окружностями (рис. 3.3).
Решением задачи является экстремаль, которая проходит через точки и . Согласно уравнению Эйлера, на экстремали интегральной член выражения (3.10) обращается в нуль, и вариация функционала примет вид
.
У
читывая,
что с точностью до бесконечно малых
высшего порядка
,
,
вариацию функционала можно записать в виде
.
Так
как
и
независимые
друг от друга вариации, то из условия
экстремума
получим условие трансверсальности
,
.
В качестве примера запишем условия трансверсальности для функционалов вида
.
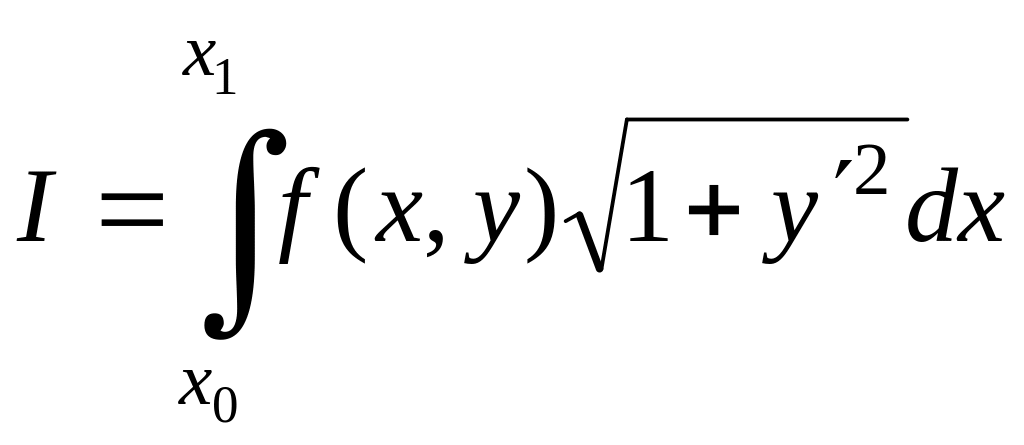В этом случае
,
и условия трансверсальности имеют вид
,
.
Отсюда
следует, что на левом конце
,
на правом -
.
Это означает, что экстремаль ортогональна
к кривым
и
,
т.е. пересекает их под прямым углом.