6.2.Алгоритмы нахождения кратчайшего пути

Здесь описаны три алгоритма нахождения кратчайшего пути – в сетях без циклов и с циклами. Первый алгоритм очень простой, но в нём представлена конструктивная идея рекурсивных вычислений. Второй алгоритм обобщает первый, однако он разработан в первую очередь для сетей, содержащих циклы. Третий алгоритм, который называется алгоритм Флойда, более общий, поскольку он позволяет одновременно найти минимальные пути между любыми двумя узлами сети.

6.2.1.Алгоритм для сетей без циклов

Сначала рассмотрим алгоритм на численном примере. Затем описанную процедуру объясним с точки зрения рекурсивных вычислений.

Пример 6.0:

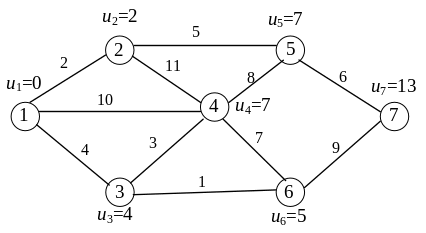
Рис. 6.11. Пример сети с циклами

Рассмотрим сеть, изображённую на рис. 6.3. Узел 1 представляет начальную точку (исходный пункт), а узел 7 – конечную точку (пункт назначения). Заметим, что сеть не имеет циклов, поскольку нет ни одной цепи, связывающей узел с самим собой.

Прежде чем описать процедуру решения, введём следующие обозначения: d_ij – расстояние на сети между смежными узлами i и j,

u_j – кратчайшее расстояние между узлами i и j, u₁ = 0.

Процедура завершается, когда получено значение u₇. Общая формула для вычисления u_j имеет вид (6.1).

(6.29)

Из этой формулы следует, что кратчайшее расстояние u_j до узла j можно вычислить лишь после того, как определено кратчайшее расстояние до каждого предыдущего узла i, соединенного дугой с узлом j.

Для узла 1 можно вычислить лишь u₂ и u₃. (Заметим, что, хотя узел 4 соединён с узлом 1 дугой, соответствующее значение u₄ вычислить нельзя, пока не будут определены u₂ и u₃.) Вычислительная схема состоит из следующих этапов.

Этап 1: u₁ = 0.

Этап 2: u₂ = u₁ + d₁₂ =0+2=2 (из 1);

u₃ = u₁ + d₁₃=0+4=4 (из 1).

Этап 3: u₄ =min{u₁+d₁₄, u₂+d₂₄ , u₃+d₃₄}= min{0+10, 2+11, 4+3}=7 (из 3).

Этап 4: u₅=min{u₂+d₂₅ , u₄+d₄₅} =min{2+5, 7+8}=7 (из 2);

u₆=min{u₃+d₃₆ , u₄+d₄₆} =min{4+1, 7+7}=5 (из 3).

Этап 5: u₇=min{u₅+d₅₇ , u₆+d₆₇} =min{7+6, 5+9}=13 (из 5).

Минимальное расстояние между узлами 1 и 7 равно 13, а соответствующий маршрут 1257. Заметим также, что решение даёт кратчайшее расстояние между узлом 1 и любым из других узлов сети.

Все вычисления можно провести непосредственно на сети (рис.6.3). Величина u_j для j узла вычисляется лишь после того, как получены u_i для всех узлов i, предшествующих j. Таким образом, начиная с u₁=0, получаем u₂ =2 и u₃ = 4. Далее можно вычислить u₄ =7. После этого определяются u₅ =7 и u₆ =5. На последнем этапе получается u₇ =13

Представленный выше тип вычислений интересен тем, что он имеет рекурсивный характер. Эти вычисления выполняются с использованием информации о всех кратчайших расстояниях до непосредственного предшествующего узла. Например, в узле 5 величина u₅ вычисляется по кратчайшим расстояниям между узлом 1 и узлами 2 и 4, т. е. u₂ и u₄ .

Заметим, что не обязательно знать конкретный маршрут, дающий кратчайшее расстояние между узлами 1 и 4. Величина u₄ включает всю информацию, необходимую для узла 4. Именно такая информация позволяет использовать рекурсивные вычисления. Рекурсивные вычисления представляют собой основу вычислительной схемы динамического программирования.