3.2.Венгерский метод решения задачи о назначениях

Специфическая структура задачи о назначениях позволяет разработать эффективный метод ее решения. Покажем, как реализуется этот метод на примере приведенной выше задачи.

Оптимальное решение задачи о назначениях не изменится, если к любой строке или столбцу матрицы стоимостей прибавить (или вычесть) постоянную величину. Этот факт можно доказать следующим образом. Если p_i и q_j вычитаются из i-й строки и j-го столбца, то новые стоимости имеют вид с_ij = с_ij – p_i – q_j. Отсюда получается новая целевая функция

.

Отсюда следует, что минимизация исходной целевой функции f приводит к такому же решению, как минимизация f .

Приведенное соображение показывает, что если можно построить новую с_ij - матрицу с нулевыми элементами, найти допустимое базисное решение, соответствующее нулевым стоимостям с_ij = 0, то такое решение будет оптимальным, поскольку стоимость не может быть отрицательной.

В табл. 48 нулевые элементы получены вычитанием наименьшего элемента в каждой строке (столбце) из соответствующей строки (столбца). Если сначала рассмотреть строки, то получим матрицу с_ij.

Таблица 48

		1	2	3
	1	0	0	4	p1=5
сij=	2	2	0	2	p2=10
	3	4	0	3	p3=13

Вычитая q₃=2 из третьего столбца, последнюю матрицу можно преобразовать так, чтобы она имела больше нулей. Таким образом, получим табл. 49.

Таблица 49

		1	2	3
сij=	1	0	2	2
	2	4	0	0
	3	2	0	1

Допустимый план:

	1	0	0
х=	0	0	1
	0	1	0

будет оптимальным: min f = p₁+p₂+p₃+q₃ = 5+10+13+12=30.

Квадратами в табл. 49 помечены элементы, соответствующие допустимому (и следовательно, оптимальному) назначению (1,1), (2,3) и (3,2) со стоимость 5+12+13=30. Заметим, что эта стоимость равна p₁+ p₂+ p₃+ q₃.

К сожалению, не всегда удается определить допустимое назначение столь просто, как в приведенном примере. Поэтому требуются другие правила для нахождения оптимального решения. Эти правила иллюстрируются на примере, приведенном в табл. 50.

Таблица 50

	1	2	3	4
1	1	4	6	3
2	9	7	10	9
3	4	5	11	7
4	8	7	8	5

Выполняя те же начальные шаги, что и в предыдущем примере, получим табл. 51.

Таблица 51

	1	2	3	4
1	0	3	2	2
2	2	0	0	2
3	0	1	4	3
4	3	2	0	0

В этом случае невозможно найти допустимое решение, состоящее из нулей. Дальнейшая процедура состоит в проведении минимального числа прямых через некоторые строки и столбцы, с тем чтобы все нули оказались вычеркнутыми. В табл. 52 показано, как используется это правило.

Таблица 52

	1	2	3	4
1	0	3	2	2
2	2	0	0	2
3	0	1	4	3
4	3	2	0	0

На следующем шаге выбирается наименьший невычеркнутый элемент (равный 1 в табл.52). Этот элемент вычитается из каждого не вычеркнутого элемента и прибавляется к каждому элементу, стоящему на пересечении проведенных прямых. В результате получается табл. 53, которая соответствует оптимальному назначению (1,1), (2,3), (3,2) и (4,4). Соответствующие суммарные затраты равны 1 + 10 + 5 + 5 = 21.

Таблица 53

	1	2	3	4
1	0	2	1	1
2	3	0	0	2
3	0	0	3	2
4	4	2	0	0

Следует заметить, что если на последнем шаге оптимальное решение не достигнуто, то процедуру проведения прямых следует повторять до тех пор, пока не будет получено допустимое решение.

В венгерском методе используется следующий принцип: оптимальность решения задачи о назначениях не нарушается при уменьшении (увеличении) элементов строки (столбца) на одну и ту же величину. Решение считается оптимальным, если все изменённые таким образом затраты с_{i j} ≥ 0, (i = ; j = ) и можно отыскать такой набор x_{i j}, что

= 0.

Алгоритм метода: Получение нулей в каждой строке. Для этого в каждой строке определяют наименьший элемент, и его значение отнимают от всех элементов строки. Переход к пункту 2. Получение нулей в каждом столбце. В преобразованной таблице в каждом столбце определяют минимальный элемент, и его значение вычитают из всех элементов этого столбца. Переход к пункту 3. Поиск оптимального решения. Находят максимальную связку, для этого просматривают строку, содержащую наименьшее число нулей. Отмечают один из нулей этой строки и зачеркивают все остальные нули этой строки и того столбца, в котором находится отмеченный нуль. Аналогичные операции последовательно проводят для всех строк. Если назначение, которое получено при всех отмеченных нулях, является полным (т.е. число отмеченных нулей равно n, что равно индексу квадратичности), то решение является оптимальным, в противном случае следует переходить к пункту 4. Поиск минимального набора строк и столбцов, содержащих все нули (минимального опорного множества). Для этого необходимо отметить: 1) все строки, в которых не имеется ни одного отмеченного нуля; 2)все столбцы, содержащие перечеркнутый нуль хотя бы в одной из отмеченных строк; 3)все строки, содержащие отмеченные нули хотя бы в одном из отмеченных столбцов. Действия 2) и 3) повторяются поочередно до тех пор, пока есть что отмечать. После этого необходимо зачеркнуть каждую непомеченную строку и каждый помеченный столбец. Цель этого шага – провести минимальное число горизонтальных и вертикальных прямых, пересекающих по крайней мере один раз все нули. Перестановка некоторых нулей. Взять наименьшее число из тех клеток, через которые проведены прямые. Вычесть его из каждого числа, стоящего в невычеркнутых столбцах и прибавить к каждому числу, стоящему в вычеркнутых строках. Эта операция не изменяет оптимального решения, после чего весь цикл расчета повторить, начиная с пункта 3.

Пример 3. 3:

Институт получил гранты на выполнение четырех исследовательских проектов. Выходные результаты первого проекта являются входными данными для второго проекта, выходные результаты второго проекта – это входные данные для третьего проекта, результаты третьего проекта используются для работы над четвертым проектом. В качестве научных руководителей проектов рассматриваются кандидатуры четырех ученых, обладающих различным опытом и способностями. Каждый ученый оценил время, необходимое ему для реализации проекта.

Матрица времен приведена ниже

Т =

В i-й строке j-м столбце матрицы Т стоит время на выполнение i-м ученым j-го проекта.

Продолжительность времени задана в месяцах. Требуется выбрать научного руководителя для выполнения каждого проекта так, чтобы суммарное время выполнения всех проектов было минимальным.

Данная задача, очевидно, является задачей о назначениях. В качестве работ рассматриваются исследовательские проекты, в качестве кандидатов – ученые, претендующие на роль научных руководителей.

Введем переменные x _{i j.}

Целевая функция задачи имеет вид

С = 3х₁₁ + 7х₁₂ + 5х₁₃ + 8х₁₄ + 2х₂₁ + 4х₂₂ + 4х₂₃ + 5х₂₄ + 4х₃₁ + 7х₃₂ + 2х₃₃ +

+ 8х₃₄ + 9х₄₁ + 7х₄₂ + 3х₄₃ + 8х₄₄ → min

Решим задачу венгерским методом, используя приведенную ниже таблицу. В i-й строке j-м столбце этой таблицы стоит время t_ij на выполнение j-го проекта i-м ученым, i= ; j= . Выберем в каждой строке минимальный элемент и запишем его в правом столбце табл. 54.

Таблица 54

№	1	2	3	4	min
1	3	7	5	8	3
2	2	4	4	5	2
3	4	7	2	8	2
4	9	7	3	8	3

Вычтем минимальные элементы из соответствующих строк, перейдем к новой таблице, в которой найдем минимальные значения в каждом столбце и запишем их в нижней строке табл. 55.

Таблица 55

№	1	2	3	4
1	0	4	2	5
2	0	2	2	3
3	2	5	0	6
4	6	4	0	5
min	0	2	0	3

Отнимем минимальные элементы из соответствующих столбцов. Перейдем к таблице 56.

Таблица 56

№	1	2	3	4
1	0	2	2	2
2	0	0	2	0
3	2	3	0	3
4	6	2	0	2

В табл. 56. сделаем назначения. Строками, содержащими наименьшее число нулей (один нуль), являются первая, третья и четвертая строки. Отметим точкой 0 первой строки. Вычеркнем 0 из первого столбца. Это вычеркивание означает, что, так как первый ученый назначен научным руководителем первого проекта, второй ученый уже не может быть назначен. Отмечаем 0 в третьей строке и вычеркиваем 0, стоящий в четвертой строке в третьем столбце, что соответствует тому, что четвертый ученый уже не может быть назначен научным руководителем тре6тьего проекта.

Отмечаем любой из нулей второй строки (действуя по порядку, отмечаем нуль, стоящий во втором столбце) и вычеркиваем нуль, стоящий в четвертом столбце. Это вычеркивание означает, что, так как второй ученый назначен научным руководителем второго проекта, то он не может быть выбран для выполнения четвертого проекта.

Число отмеченных нулей равно 3, т.е. назначение не является полным. Перейдем к пункту 4 алгоритма.

Найдем минимальный набор строк и столбцов, содержащий все нули (табл.57.).

Таблица 57

№	1	2	3	4
1	0	2	2	2
2	0	0	2	0
3	2	3	0	3
4	6	2	0	2

Отмечаем точкой четвертую строку, не содержащую ни одного отмеченного нуля. Отметим третий столбец, содержащий перечеркнутый нуль в четвертой строке. Отметим третью строку, содержащую отмеченный нуль в третьем столбце. Кроме третьего столбца, больше нет столбцов, содержащих перечеркнутые нули в отмеченных строках. Вычеркиваем отмеченный столбец и неотмеченные строки. В оставшихся клетках минимальный элемент равен 2. Вычтем его из каждого числа невычеркнутых (1, 2, 4) столбцов. Получим табл. 58.

Таблица 58

№	1	2	3	4
1	-2	0	2	0
2	-2	-2	2	-2
3	0	1	0	1
4	4	0	0	0

Теперь прибавим 2 к каждому числу вычеркнутых строк в преобразованной таблице. Получим табл. 59.

Таблица 59

№	1	2	3	4
1	0	2	4	2
2	0	0	4	0
3	0	1	0	1
4	4	0	0	0

Вновь сделаем назначение, отметив по порядку нули в табл. 59. Это назначение является полным, так как число отмеченных нулей равно 4. Получено следующее назначение:

x11 = 1	первый ученый назначается научным руководителем первого проекта;
x22=1	второй ученый – научный руководитель второго проекта;
x33=1	третий ученый – научный руководитель третьего проекта;
x44 =1	четвертый ученый – научный руководитель четвертого проекта.

Время выполнения четырех проектов: C = 3 + 4 + 2 + 8 = 17.

Данное назначение не единственное. Если во второй строке сначала отметить не второй, а четвертый нуль, получим следующее назначение (табл.60).

Таблица 60

№	1	2	3	4
1	0	2	4	2
2	0	0	4	0
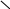
3	0	1	0	1
4	4	0	0	0

x11 = 1	первый ученый назначается научным руководителем первого проекта;
x24=1	второй ученый руководит четвертым проектом;
x33=1	третий ученый руководит третьим проектом;
x42 =1	четвертый ученый руководит вторым проектом.

Время на выполнение проектов не изменилось:

С = 3·1 + 5·1 + 2·1 + 7·1 = 17.

Таким образом, получены два оптимальных назначения, которым соответствует минимальное время выполнения.

Заметим, что результат, полученный по венгерскому методу, не изменится, если в алгоритме заменить строки на столбцы, и наоборот.

Пример 3. 4:

Для выполнения 4-х видов землеройных работ могут быть использованы экскаваторы 4-х типов. Производительность i-го типа экскаватора при выполнении j-ой работы задается матрицей.

	0 ,9	0,6	0,7	0 ,9
	0,7	0,8	0,9	0,8
С=	0,8	0,6	0,8	0,9
	0,8	0,7	0,9	0,7

Учитывая, что на каждой из работ может быть занят только лишь один экскаватор, и что все экскаваторы должны быть задействованы. Найти такое распределение экскаваторов между работами, которое обеспечивает максимальную производительность.

Обозначим

f=

; j=1, 2,..,4 (j-я работа выполняется только одним экскаватором);

; i=1, 2,..,4 (i-й экскаватор выполняет только одну работу);

x_ij={0;1}

Чтобы использовать венгерский метод перейдем от задачи максимизации к задаче минимизации противоположной целевой функции:

махf=min(-f)=min , т. е. умножим себестоимости на (-1) (табл. 61).

Таблица 61

	-0,9	-0,6	-0,7	-0,9	р1=-0,9
С=	-0,7	-0,8	-0,9	-0,8	р2=-0,9
	-0,8	-0,6	-0,8	-0,9	р3=-0,9
	-0,8	-0,7	-0,9	-0,7	р4=-0,9

Вычтем р_i (р_i = ) из i-й строки (i=1, 2, . . . ,4), получим табл. 62.

Таблица 62

	0	0,3	0,2	0
С'=	0,2	0,1	0	0,1
	0,1	0,3	0,1	0
	0,1	0,2	0	0,2

Вычтем из второго столбца: q₂= , тогда получим табл. 63.

Таблица 63

					ai
	0	0,2	0,2	0		1
С=	0,2	0	0	0,1		1
	0,1	0,2	0,1	0		1
	0,1	0,1	0	0,2		1
bj	1	1	1	1

В табл. 63. сделаем назначения. Строками, содержащими наименьшее число нулей (один нуль), являются третья и четвертая строки. Отметим точкой 0 третей строки и положим х₃₄=1, вычеркнем 0 из четвертого столбца.

Отмечаем 0 в четвертой строке, полагая х₄₃=1 и вычеркиваем 0, стоящий во второй строке и в третьем столбце. Остается положить х₁₁=1 и х₂₂=1.

maxf=0,9·1+0,8·1+0,9·1+0,9·1=3,5.