Поверхности b-spline: Построение

Дана следующая информация:

1. набор из m+1 рядов из n+1 контр. точек p_i,j, где 0 <= i <= m и 0 <= j <= n;

2. узловой вектор из h + 1 узлов в направлении u, U = { u₀, u₁, ...., u_h };

3. узловой вектор из k + 1 узлов в направлении v, V = { v₀, v₁, ...., v_k };

4. степень p в направлении u; и

5. степень q в направлении v;

поверхность B-spline, описываемая этой информацией, имеет следующий вид:

где N_i,p(u) и N_j,q(v) - это базисные функции B-spline степеней p и q, соответственно. Заметьте, что должны выполняться фундаментальные тождества, по одному на каждое направление: h = m + p + 1 и k = n + q + 1. Таким образом, поверхность B-spline - это еще один пример поверхностей [tensor] произведения.

Следующий рисунок показывает поверхность B-spline, определяемую 6 рядами и 6 столбцами контр. точек.

Узловой вектор и степень в направлении u равны U = { 0, 0, 0, 0.25, 0.5, 0.75, 1, 1, 1 } и 2. В направлении v это V = { 0, 0, 0, 0, 0.33, 0.66, 1, 1, 1, 1 } и 3.

Базисные Функции

Коэффициент контр. точки p_i,j - это произведение двух одномерных базисных функций B-spline, одна в направлении u, N_i,p(u), а другая - в направлении v, N_j,q(v). Все эти произведения - это двумерные функции B-spline. Следующие рисунки показывают базисные функции контр. точек p_2,0, p_2,1, p_2,2, p_2,3, p_2,4 и p_2,5.

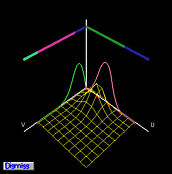
Двумерные базисные функции показаны в виде сеточных поверхностей. Так как контр. точки лежат на одном ряду, базисная функция в направлении u фиксирована, тогда как базисные функции в направлении v изменяются. Так как базисные функции B-spline в общем случае не равны нулю на нескольких последовательных узловых интервалах (схема локального изменения), двумерные базисные функции B-spline не равны нулю на пересечении[произведении?] двух узловых интервалов, на которых хотя бы одна одномерная базисная функция не равна нулю. Этот факт ясно виден на рисунках выше.

Фиксированные, Закрытые и Открытые Поверхности b-spline

Так как кривая B-spline может быть фиксированной, закрытой или открытой, то и поверхность B-spline также может быть трех типов в каждом направлении. То есть, можно узнать, является ли поверхность B-spline фиксированной в направлении u и закрытой в направлении v. Если B-spline фиксирована в обоих направлениях, то такая поверхность проходит через контр. точки p_0,0, p_m,0, p_0,n и p_m,n и касательна восьми сегментам контрольной сетки в этих четырех точках. Если поверхность B-spline закрыта в каком-то направлении, то все изопараметрические кривые в этом направлении являются закрытыми кривыми и поверхность становится трубой. Если поверхность B-spline открыта в обоих направлениях, то поверхность не проходит через контр. точки p_0,0, p_m,0, p_0,n и p_m,n. Эти замечания заостряют внимание только на поверхностях, фиксированных в обоих направлениях. Следующие рисунки показывают три поверхности B-spline: фиксированную, закрытую и открытую в обоих направлениях. Все три поверхности определяются одним и тем же набором контр. точек; но, как в случае с кривыми B-spline, их узловые векторы отличаются.