Неявные Поверхности
Вернемся к неявным поверхностям. Неявные поверхности очень удобны для моделирования. Например, пусть даны две поверхности и нам нужно найти третью, являющуюся плавным переходом между ними. Этот процесс называется стыковкой, а третья поверхность - стыковочной поверхностью для данных поверхностей. Эта стыковочная поверхность, конечно, не единственная, и обычно имеет неявный вид. Следующий рисунок показывает стыковочную поверхность (желтая), соединяющую поверхности, показанные синим и зеленым.
Фактически, во многих случаях алгебраические поверхности очень полезны. Хороший пример - классификация точек. Классификация точек определяет, какие из точек находятся внутри, снаружи или на поверхности. Непросто разработать алгоритм для параметрической поверхности; тогда как для неявных поверхностей это несложная задача. Пусть дана точка (a,b,c) и неявная поверхность p(x,y,z)=0. Тогда, если p(a,b,c) больше, равно или меньше нуля, то точка (a,b,c) лежит соответственно снаружи поверхности, на ней или внутри нее.
Можно легко найти нормальный вектор для алгебр. пов-ти. Фактически, нормальный вектор для поверхности p(x,y,z) = 0 - это просто ее градиент:
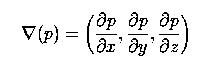
Когда будет найден нормальный вектор в точке, касательную плоскость будет найти просто.
К сожалению, отображение алгебраической поверхности - не легкая задача. Самый простой и самый неэкономный по времени способ - это отслеживание лучей. Многие программы, предназначенные для этого, предлагают юзеру ввести неявное уравнение. Хорошими примерами являются POVRAY и Radiance. Тем не менее, отслеживание лучей очень медленно. Другой путь - разделение поверхности на треугольники ("триангуляция") наподобие того, что было в параметрических поверхностях. Для неявных поверхностей, тем не менее, дело обстоит по-другому, так как нет определенной области, которую можно было бы делить на треугольники. Говоря точнее, триангуляция должна проводиться прямо на поверхности. Программы, которые могут разбивать неявные поверхности на полигоны (не обязательно треугольники) обычно называют полигонизаторами [polygonizers]. Разработка таких программ - работа для настоящих извращенцев :)
Следующие поверхности получены с помощью известного полигонизатора от [Jules Bloomenthal] , который включен в нашу поверхностную систему. Поверхность слева - это гиперболический параболоид, а справа - циклоид кольца [Dupin] с рациональной поверхностью 4 степени. Две эти поверхности разкладываются на большое количество маленьких треугольников, каждый из которых раскрашивается случайным цветом. Тем не менее, необязательно использовать такое большое количество треугольников.
Особенности
Основной проблемой этих полигонизаторов является то, что большинство из них не очень хорошо работают с особыми точками. Точка на параметрической или неявной поверхности называется особой, если в ней все частные производные [partials] равны нулю. Особые точки - это часть самопересечения поверхности или ее острые края. Следующие рисунки показывают разные типы особых точек.
Первая поверхность - третьей степени, ее уравнение
x2 + y3 - y2 + z2 = 0
Градиент этой поверхности равен
( 2x, 3y2 - 2y, 2z )
Таким образом, (0,0,0) - это особая точка, так как в этой точке все составляющие градиента равны нулю. Она показана на рисунке. Заметьте, есть еще одна особая точка - (0,2/3,0).
На среднем рисунке поверхность имеет уравнение
-x3 + 2xz - yz2 = 0
Ее градиент равен
( -2x2 + 2z, -2yz, 2x - y2 )
Из второй составляющей, имеем либо y = 0, либо z = 0. Если y = 0, то третья составляющая дает x, равное нулю, и, следовательно, первая составляющая дает z, равное нулю. Если z = 0, то первая составляющая дает x, равное нулю, а третья составляющая дает y, равное нулю. В обоих случаях получаем особую точку (0,0,0).
Хотя в двух первых случаях были отдельные особые точки, они могут лежать на прямой или даже кривой. Вот, например, на правом рисунке поверхность имеет уравнение
-x2y + x2 - yz2 - z2 = 0
У нее вектор градиента равен
( -2xy+2x, -(x2+z2), -2z )
Если z = 0, то из второй составляющей получаем, что x также должен быть равен нулю. Если и x, и z - нули, то первая составляющая также будет равна нулю не зависимо от значения y. Это значит, что из-за того, что x = z = 0, а y имеет произвольное значение, получаем особую точку. Таким образом, ось y содержит все особые точки. Рисунок показывает три прямых. Все они лежат на поверхности; тем не менее, вертикальная прямая - это ось y, которая также является линией самопересечения, на которой лежат все особые точки.