Nurbs: Изменение Весов

Так как кривые NURBS определяются набором контр. точек, узловым вектором, значением степени и набором весов, то имеем еще один важный параметр для изменения формы кривой - это значения весов. Вспомним, что базисные функции кривых NURBS - это

Таким образом, увеличение и уменьшение значения w_i соответственно увеличит и уменьшит значение R_i,p(u). Говоря точнее, увеличение значения w_i приблизит кривую к контр. точке p_i. Фактически, все зависимые от этого точки на кривой также приблизятся в направлении к p_i. Когда w_i станет равно бесконечности, кривая пройдет через контр. точку p_i. С другой стороны, уменьшение значения w_i отодвинет кривую от контр. точки p_i. Нажмите сюды для более глубокого обсуждения.

Следующие рисунки показывают кривую NURBS 6 степени и ее базисные функции. Выбранная контр. точка - p₉. На первом рисунке все весы равны 1 и поэтому кривая является кривой B-spline. На втором рисунке w₉ увеличено до 2 и, как видите, часть кривой двигается ближе к p₉. Так как w₉ увеличилось, то же самое и с R_9,6(u), как показано на рисунке справа.

Далее w₉ увеличивается до 5, 10 и 20, соответствующее R_9,6(u) становится больше, и несет больший вес. Это пододвигает кривую ближе к контр. точке p₉. Когда w₉ = 20, кривая очень близка p₉.

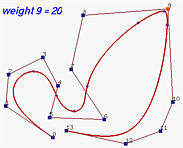
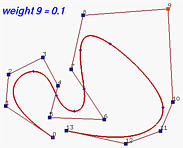
Взглянем на противоположный эффект.Вот начальный случай, когда все весы равны 1. Далее, w₉ уменьшается до 0.5 и это отодвигает кривую от контр. точки p₉. Заметьте, что соответствующее R_9,6(u) уменьшается, как и влияние контр. точки p₉ на кривую p(u). Когда w₉ изменяется до 0.1, кривая отодвигается и значение R_9,6(u) становится меньше. Последний рисунок показывает кривую при w₉ равном нулю. Так как R_9,6(u) равно нулю, то оно не влияет на кривую и в результате отрезок кривой напротив контр. точки p₉ плоский.

В итоге, имеем следующее:

Увеличение (соотв., уменьшение) значения веса w_i пододвигает (соотв. отталкивает) кривую к (соотв., от) контр. точке p_i. Когда значение w_i уходит в бесконечность, кривая проходит через контр. точку p_i, а когда значение w_i равно нулю, контр. точка p_i не влияет на кривую.

Углубленное Рассуждение

Раасмотрим пристальнее влияние изменения веса выбранной контр. точки. Давайте вернемся к определению кривой NURBS:

Выберем контр. точку p_k и исследуем влияние изменения w_k. Так как p_k может влиять на кривую p(u) только на ненулевой области ее коэффициента N_k,p(u) (т.e. [u_k, u_k+p+1)), то далее примем, что u лежит на [u_k, u_k+p+1).

Вынесем члены с w_k из суммирования, получим:

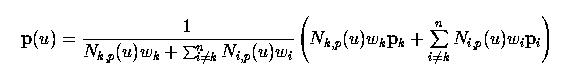
Так как это уравнение довольно сложное, упростим его следующим способом:

Теперь уравнение стало таким легкочитаемым:

Сначала возьмем случай w_k = 0. Имеем A = 0, и точка на кривой, обозначается как p⁰(u), равна

Теперь давайте вычислим вектор из этой "базисной" точки p⁰(u) в соответствующую ей точку p(u) для произвольного w_k. После простых преобразований имеем следующее:

Что это значит? Это значит, что вектор p(u)-p⁰(u) и вектор p_k-p⁰(u) имеют одно направление, а длина первого в A/(A+B) больше, чем длина последнего для каждого u на [u_k, u_k+p+1)! Так как точки p_k и p⁰(u) фиксированы, то можно сказать, что p(u) лежит на прямой от p_k до p⁰(u). Более того, если все весы неотрицательны, то и A, и B неотрицательны и значение A/(A+B) лежит между 0 и 1! То есть, точка p(u) лежит на отрезке между p_k и p⁰(u).

Что, если w_k достигает бесконечности? Давайте поделим числитель и знаменателm кривой p(u) на w_k, как показано ниже.

Если w_k уходит в бесконечность, 1/w_k становится нулем. Отсюда, если w_k достигает бесконечности, то p(u) достигает p_k, выбранной контр. точки. Вот итог сказанного:

Если wk неотрицательно, то p(u) всегда лежит на отрезке между p0(u) и pk, где p0(u) - это точка, соответствующая wk = 0, а u лежит на [uk, uk+p+1). Более того, когда wk изменяется от 0 до бесконечности, p(u) двигается от p0(u) к pk, а если wk - бесконечность, то p(u) становится pk.

Следующий рисунок иллюстрирует этот результат. Имеем кривую NURBS 6 степени, определенную по 9 контр. точкам (n = 8) и 16 узлам (m = 15), как показано ниже.

u0 = u1 = u2 = u3 = u4 = u5 = u6	u7	u8	u9 = u10 = u11 = u12 = u13 = u14 = u15
0	1/3	2/3	1

Выбранная контр. точка - это p₄. Так как коэффициент при p₄, N_4,6(u), не рваен нулю на [u₄, u₄₊₆₊₁) = [0,1), то изменение w₄ влияет на кривую целиком!

Точки, соответствующие u = 1/3 и u = 2/3 обозначены на кривой разными цветами. Кривая, соответствующая w₄ = 0 - самая нижняя, обозначена 0. Риснуок показывает кривые для w₄, равного 2, 3, 4, 5, 10, 20 и 50. При увеличении значения w₄ кривая пододвигается ближе к контр. точке p₄. Когда w₄ увеличивается до 50, кривая становится очень близко к p₄. Пожалуйста, заметьте, что все точки, соовтетствующие p(1/3) находятся на отрезке прямой между точками p⁰(1/3) и p₄, а все точки, соответствующие p(2/3) - на отрезке прямой между p⁰(2/3) и p₄. Также заметьте, что отрезок кривой между точками p(1/3) и p(2/3) становится короче при увеличении значения w₄. В конце концов длина этого криволинейного отрезка становится равной нулю (т.e. p(1/3) и p(2/3) становится равно p₄), когда w₄ равно бесконечности. Можете ли вы обобщить это наблюдение?