Кривые b-spline: Определение

Дано n + 1 контрольных точек p₀, p₁, ..., p_n и узловой вектор U = { u₀, u₁, ..., u_m }, кривая B-spline степени p, определяемая этими точками и узловым вектором U, это

,

где N_i,p(u) - это базисные функции кривой B-spline степени p. Вид кривой B-spline очень похож на кривые Безье. В отличие от кривых Безье, кривые B-spline требуют больше информации, а именно: набор контр. точек, узловой вектор, и степень. Заметьте, что n, m и p должны удовлетворять условию m = n + p + 1. Точнее, если мы хотим описать кривую B-spline степени p с n + 1 контр. точками, нам нужно обеспечить [supply] n + p + 2 узлов u₀, u₁, ..., u_n+p+1. С другой стороны, если узловой вектор состоит из m + 1 узлов и дано n + 1 контр. точек, то степень кривой B-spline равна p = m - n - 1.

Хотя N_i,p(u) похоже на B_n,i(u), степень кривых B-spline - это входные данные, тогда как степень кривой Безье зависит от количества контр. точек. Поэтому, чтобы изменить форму кривой B-spline, можно изменить один или несколько управляющих параметров: положения контрольных точек, положения узлов, степень кривой.

Если узловой вектор не имеет конкретной структуры, полученная кривая не будет касаться первого и последнего сегмента контрольной ломаной, как показано на рисунке ниже. Этот тип кривых B-spline называется открытыми кривыми B-spline. Мы, возможно, захотим закрепить кривую, то есть сделать так, чтобы она была касательна первому и последнему сегментам, как в случае с кривыми Безье. Чтобы это сделать, первый и последний узлы должны повторяться p+1 раз (т.e., быть множественности p+1). Таким образом, получим так называемую фиксированную кривую B-spline. Посмотрите на средний рисунок ниже. Дублируя некоторые узлы и контрольные точки, можно сделать полученную кривую замкнутой. В этом случае начало и конец полученой кривой соединяются, образуя замкнутую петлю, как показано на правом рисунке ниже. Таким образом получаем фиксированную кривую. [In this note, we shall use clamped curve.]

На этих рисунках по n+1 контр. точек, где n=9 и p = 3. То есть, m должно быть равно 13, чтобы узловой вектор содержал 14 узлов. Чтобы получить эффект фиксированности, првые p+1 = 4 и последние 4 узла должны быть одинаковыми. Остальные 14 - (4 + 4) = 6 узлов могут мыть распределены где угодно в области определения. Фактически, кривая образуется узловым вектором U = { 0, 0, 0, 0, 0.14, 0.28, 0.42, 0.57, 0.71, 0.85, 1, 1, 1, 1 }. Заметьте, что, кроме первых и последних четырех узлов, средние узлы почти равномерно распределены. Рисунки также показывают соответствующие отрезки кривой для каждого узлового интервала. Фактически, маленькие треугольники - это точки на кривой, соответствующие узлам. Так как у нас только шесть узлов не на концах, то есть шесть маленьких треугольников, указывающих положения соответствующих узлов.

Как упоминалось ранее, если на концах нет повторяющихся узлов, то полученная кривая не будет касательна к первому и последнему сегментам. В этом случае нужно позаботиться об одном дополнительном ограничении. На предыдущей странице мы рассмотрели пример вычисления базисной функции с узловым вектором U = { 0, 0.25, 0.5, 0.75, 1 }, где m = 4. Если базисные функции степени 1 (т.e., p = 1), то имеется три базисные функции N_0,1(u), N_1,1(u) и N_2,1(u), как показано ниже.

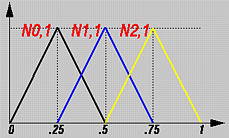
Так как это узловой вектор не фиксирован, то первый и последний узловые интервалы (т.e., [0, 0.25) и [0.75, 1) ) имеют только одну ненулевую базисную функцию, тогда как второй и третий интервалы (i.e., [0.25, 0.5) и [0.5, 0.75) ) имеют две ненулевые базисные функции. Вспомним из важных свойств B-spline, что на узловом интервале [u_i, u_i+1) есть максимум p+1 ненулевых базисных функций степени. Таким образом, в этом примере, узловые интервалы [0,0.25) и [0.75,1) не имеют "полной поддержки" ["full support"] базисных функций. В общем случае, для степени p, интервалы [u₀, u_p) и [u_n-p, u_n) не будут иметь "полной поддержки" базисных функций и будут отбрасываться в случае открытой кривой B-spline. Таким образом, получаем следующее важное замечание:

Для открытых кривых B-spline, область определения - это интервал [u_p, u_n-p].