VI. Статика

50. Графічне зображення сил.

Сили, що діють на тіло, можуть відрізнятися одна від одної і величиною, і напрямом. Штовхаючи з більшою чи меншою силою футболь ний м'яч, ми надаємо йому більшої або меншої швидкості. Залежно від на­пряму діючої сили футбольний м'яч летить у тому чи іншому напрямі. Має також значення точка прикладання сили — точка тіла, на яку діє сила. Справді, якщо ми прив'яжемо мотузку в точці маховика (рис. 47) і натягатимемо її в напрямі , то маховик повернеться. Навпаки, якщо ми прив'яжемо мотузку в точці і з такою силою тягтимемо її в тому самому напрямі, то такого руху маховика не буде.

Щоб визначити силу, ми повинні знати: 1) величину сили, 2) її напрям, 3) точку її прикладання.

Точку прикладання сили можна перенести в будь-яку точку тіла в напрямі сили. Ми можемо надати руху маховикові, якщо прив'яжемо в точці довшу мотузку і тягтимемо її за кінець у попередньому напрямі, або прикріпимо до точки шток і штовхатимемо цей шток у тому таки напрямі . Паровоз, що тягне поїзд, можна причепити і на початку поїзда, і в його хвості, і всередині, при цьому дія сили не зміниться.

Сили, як векторні величини, зображуються різної величини відрізками прямої з стрілкою на кінці. Починається відрізок у точці прикладання сили (рис. 47).

51. Додавання сил, що діють в напрямі однієї прямої.

Коли на тіло діє яка-небудь одна сила, то воно рухається в напрямі прикладеної сили. Якщо на тіло діє не одна, а дві або кілька сил у різних напрямах, то тіло або залишається в спокої, або набуває руху, який може спричинити одна сила в якомусь цілком певному напрямі.

Сила, що діє на тіло так само, як дві або кілька сил, взятих разом, називається рівнодійною даних сил.

Ті сили, що ми замінюємо рівнодійною силою, називаються складовими.

Відшукання рівнодійної за даними складовими називають додаванням сил.

Розглянемо на прикладі, як додавати сили, що діють на тіло в напрямі однієї прямої.

Приклад 1. Поїзд рухається подвійною тягою. Сила тяги одного з паровозів дорівнює кг, другого кг. Знайти рівно дійну сил і

Розв'язання. Рівнодійна тобто сумі сил скла­дових.

Приклад 2. Камінь, що важить кг, падає у повітрі. Опір повітря — кг. Знайти рівнодійну сил ваги й опору.

Розв'язання. Очевидно, у даному разі — тобто рівнодійна дорівнює різниці сил складових і йде в напрямі більшої сили.

Рівнодійна двох або кількох сил, що діють на напрямі тієї самої прямої лінії, дорівнює алгебричній сумі сил складових.

52. Додавання двох сил, прикладених до однієї точки під кутам одна до одної.

Рівнодійна двох сил, прикладених до однієї точки тіла під кутом одна до одної, величиною і напрямом дорівнює діагоналі паралелограма, побудованого на цих силах.

На рис. 48 подано приклад додавання двох сил і що діють на точку тіла під кутом одна до одної. Будуючи на даних силах паралелограм , знайдемо діагональ цього паралелограма , що й величиною й напрямом відповідає рівнодійній сил і

У тому випадку, коли дані сили лежать в одній площині, але прикладені не до однієї точки, а до двох різних точок тіла — і (рис. 49), ми визначимо рівнодійну сил таким способом. Продовжуючи напрями даних сил, знайдемо точку , де вони перетинаються. Переносячи в цю точку точки прикладання сил і (рис. 51), визначаємо за правилом паралелограма рівнодійну

Діагональ паралелограма визначається або графічно за масштабом, або обчисленням за допомогою тригонометрії.

Для найпростішого випадку, коли дві сили і , діють під прямим кутом одна до одної (рис. 50) їхню рівнодійну можна обчислити за теоремою Піфагора.

Щоб обчислити величину сили в загальному виді, треба застосувати теорему з тригонометрії: квадрат сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін на косинус кута між ними.

Позначивши кут між силами і (рис. 51) буквою , з трикутника дістанемо: , але . Через це

.

В окремому випадку, коли сили напрямлені в один бік, то

тобто:

Якщо сили і розміщені під кутом 90°, то

Якщо сили напрямлені протилежно, то ,

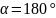звідси:

Щоб визначити напрям рівнодійної сили, застосуємо до трикутника теорему: сторони трикутника пропорційні синусам протилежних кутів. Позначивши кут між силами і буквою дістанемо:

але ; через це:

. .

Отже, рівнодійна визначена і величиною, і напрямом.

Приклад 1. Дано дві сили: кг і 4 кг, що діють під прямим кутом. Знайти рівнодійну.

Розв'язання. Будуємо паралелограм сил, що на цей раз є прямокутник, і обчислюємо за теоремою Піфагора:

кг.

Вправа.

1. Нарисувати такий випадок додавання двох сил під кутом, коли рівнодійна де менша за кожну із складових.

2. Між якими границями змінюється рівнодійна двох сил і , прикладених до точки під кутом, залежно від величини кута.