39.Кутова швидкість.

Колесо обертається навколо нерухомої осі (рис. 40). Розглянемо рух окремих точок 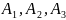і т. д. цього колеса. За той самий проміжок часу, наприклад за одну секунду, вони описуватимуть дуги різних радіусів, а, значить, шлях їх за одну секунду і лінійні швидкості будуть різні. Максимальну лінійну швидкість буде мати точка , що є на самім колі колеса, мінімальну — точка, що є на осі, де . Отже, лінійною швидкістю окремих точок не можна схарактеризувати швидкості обертання колеса в цілому.

Для характеристики руху обертального тіла запроваджується особливу величину — кутову швидкість.

Кутова швидкість вимірюється кутом, на який обертається тіло за одну секунду.

У техніці швидкість обертання маховика та шківів прийнято виміряти кількістю оборотів за хвилину. Наприклад, кажуть: швидкість шківа молотарки —1070 оборотів за хвилину. Швидкість якора електромотора —1500 оборотів за хвилину, Швидкість маховика нафтового двигуна — 300 оборотів за хвилину,

В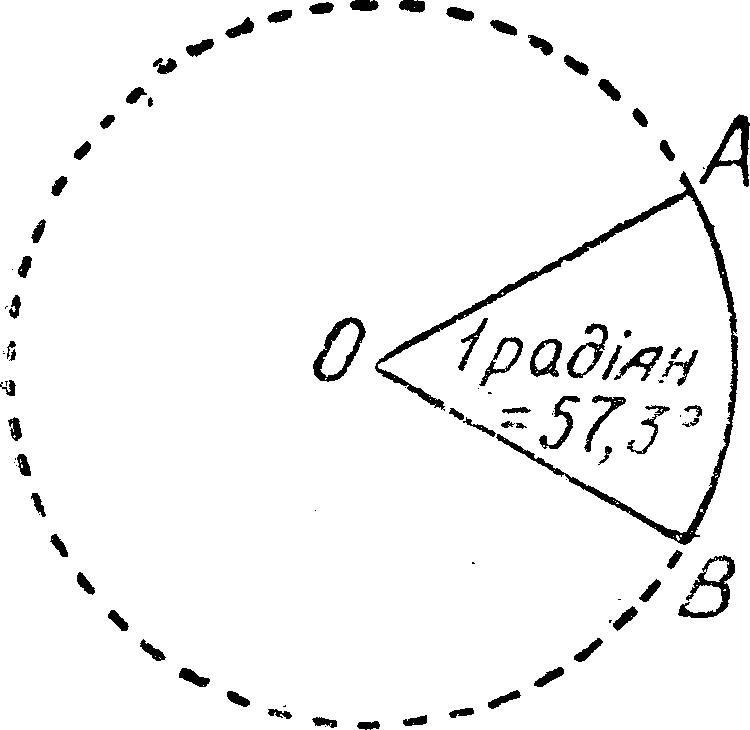 елементарній геометрії кути виміряються градусами. Крім виміру кута градусами, є інша одиниця, для вимірювання кутів — радіан, тобто центральний кут, довжина дуга якого дорівнює радіусові (рис. 31).

У градусній мірі радіан 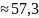градуса.

З

Рис. 31

а одиницю кутової швидкості у фізиці прийнято 1 радіан за секунду (позначається .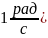

Ціле коло має в собі 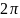радіанів, а тому число обертів за хвилину неважко пере­вести на число радіанів за секунду.

Приклад. Швидкість маховика — 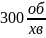. Обчислити кутову швидкість у .

Число обертів за секунду 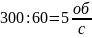. Кутова швидкість дорівнює .

Кутова швидкість позначається грецькою буквою 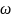(омега).

Отже, в загальному вигляді 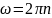: де — число оборотів тіла за одну секунду. Якщо позначити буквою час, протягом якого відбувається один оборот, то кутова швидкість може бути виражена формулою:

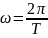
40.Залежність між лінійною й кутовою швидкістю.

Нехай ми маємо кутову швидкість ю точки, що рухається по колу. Визначимо, чому дорівнює лінійна швидкість цієї самої точки. В § 39 ми вивели формулу лінійної швидкості:

Підставивши в неї значення , дістанемо:

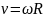
де — радіус круга, а число , тобто лінійна швид­кість дорівнює радіусові, помноженому на кутову швидкість. З цієї формули дістанемо:

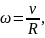
тобто кутова швидкість в радіанах дорівнює лінійній швидкості, поділеній на радіус.

Запитання.

1. Що таке кутова швидкість?

2. Якими одиницями виміряється лінійна і кутова швидкість?

3. Яке співвідношення між лінійною і кутовою швидкістю?

4. Виразити радіанами кутову швидкість добового обертання Землі.

5. Обчислити лінійну швидкість точки екватора. (Вважати, що земної кулі дорівнює 6400 км).

6. Обчислити лінійну швидкість точки земної кулі на широті .

41.Напрям швидкості тіла, що рухається по колу.

Ми знаємо, що швидкість є вектор, тобто величина, яка має напрям. При прямо­лінійному русі швидкість зображується стрілкою, напрямленою по лінії руху.

Рис. 32

Рис. 34

Рис. 33

Подивимося, як зобразити вектором швидкість у будь-якій точці шляху при криволінійному, зокрема коловому, русі. Візьмемо камінь, прив'язаний до шнура, і почнемо його обертати (рис. 32). Камінь рухатиметься по колу. Якщо в певний момент ми випустимо з рук шнур або він увірветься, то камінь летить по дотичній лінії з тією швидкістю, яку він мав на колі (рис. 33).

Так само по дотичній до кола колеса летять грудки грязюки, відірвавшись від автомобільного або велосипедного колеса, іскри від гострильного каменя (рис. 34). Швидкість тіла, що рухається по колу, напрямлена по дотичній у даній точці кола.

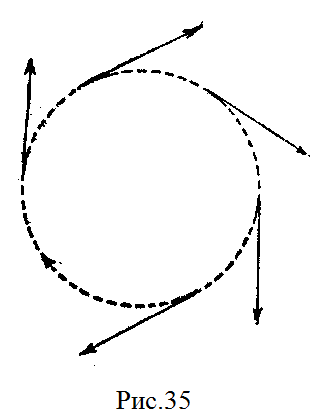Швидкість тіла, що рухається по колу, зображується вектором, дотичним до кола в даній точці (рис. 35).

При рівномірному русі по колу всі вектори швидкості рівні між собою величиною, але відмінні напрямом.

Доцентрове прискорення.

Повернемося до досліду з каменем, що обертається на шнурі. Увімкнувши між рукою і к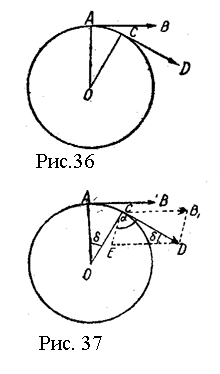 аменем пружинний динамометр, ми можемо вимірити величину сили взаємодії між каменем і рукою.

Сила, що удержує обертальне тіло на колі називається доцентровою силою. Через те, що швидкість тіла, яке рухається по колу, у різних точках кола має різні напрями, ми повинні зробити висновок, то швидкість тіла змінюється напрямом.

При переході точки з положення в положення (рис. 36) швидкість точки змінилася. У точці швидкість зображується вектором , у точці — вектором 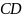. Віднімаючи від вектора вектор (за правилом паралелограма), ми знайдемо зміну швидкості за час 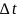протягом якого точка перейшла з положення в положення . Поділивши добуту різницю на час, знайдемо прискорення під впливом доцентрової сили, або доцентрове прискорення.

Нехай точка, рухаючись рівномірно, перейшла з в пройшовши дуже малий шлях 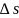по дузі протягом часу (рис. 37). Швидкість у точці зобразиться вектором , у точці - вектором .

Величиною дорівнює тому, що рух по колу рівномірний, але і відмінні напрямом. Віднімаємо від вектора вектор за правилом паралелограма швидкостей.

Для цього переносимо у точку , дістаємо лінію 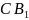і будуючи на , як на діагоналі, паралелограм, одна з сторін якого дорівнює знаходимо вектор 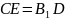що є різниця векторів і

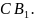
Через те, що час і ми взяли надзвичайно малий, то дуга буде близька до хорди .

Вважаючи сектор 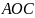за трикутник (через малу величину дуги ), бачимо, що трикутники 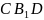і подібні, тому, що і рівні між собою, як кути з взаємно перпендикулярними сторонами.

З подібності трикутників виходить:

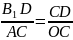
Позначимо приріст швидкості через шлях — через , величину вектора — буквою , — буквою ; підставивши ці позначення в пропорцію, маємо:

Через те що обертовий рух відбувається рівномірно, за час точка пройде шлях

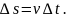
Підставляючи значення у попередню формулу, отримаємо:

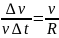
Звідки:

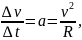оскільки .

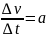тобто прискорення при рівномірному русі по колу дорівнює квадратові швидкості точки, що рухається по колу, поділеному на радіус круга.

Щоб знайти напрям прискорення, розглянемо трикутник . Кут 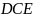між напрямом швидкості і напрямом при­скорення , .

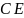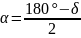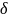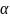Що менший проміжок часу, за який змінюється швидкість, то менша дуга і кут . В міру зменшення кута кут на наближається до . В кожний даний момент прискорення перпендикулярне до швидкості, значить, доцентрове прискорення спрямоване по радіусу до центра круга.