37.Рух тіла, кинутого під кутом до горизонту.

З точки під кутом до горизонту кинуто з певною початковою швидкістю тіло (рис. 28).

Розглянемо, як рухатиметься це тіло. Припустимо,що початкова швидкість тіла напрямлена по прямій . Якби на тіло не діяла сила тяжіння,то воно стало б за інерцією рухатися рівномірно прямою , проходячи за послідовні секунди рівні шляхи: 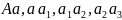і т. д. Насправді ж на тіло діє сила він з руху за інерцією та падіння. За першу секунду після початку руху тіло за інерцією пройшло б шлях , але за той самий час, падаючи, воно переміститься в напрямі вниз на відстань 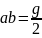. Дійсне положення тіла наприкінці першої секунди буде в точці . Міркуючи аналогічно, знайдемо, що наприкінці другої секунди тіло буде в точці пройшовши за інерцією шлях, рівний і від дії сили тяжіння шлях . Через три секунди тіло буде в точці пройшовши по шлях і одночасно впавши на 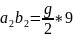і т. д., поки тіло впаде на землю. З’єднуючи добуті точки, відшукаємо криву, якою рухається тіло. Це також парабола.

Дана парабола відмінна від знайденої нами при розгляді руху тіла, кинутого горизонтально, лише своєю формою.

Відстань , тобто відстань від точки початку льоту до точки падіння, відлічувана в горизонтальному напрямі, називається далекістю льоту.

Відстань від горизонту до вищої точки польоту її називається висотою льоту.

Далекість польоту залежить від кута між напрямом, у якому кидають тіло, та горизонтом і від швидкості вильоту. Теоретично найбільша далекість польоту буває при куті .

Запитання та вправа.

1. Яким шляхом рухається тіло, кинуте під кутом до горизонту?

2. Що називається далекістю льоту?

3. Що називається висотою льоту ?

4. При якому куті буває максимальна далекість льоту?

5. Побудувати траєкторію руху тіла, кинутого з певною початковою швидкістю під кутом до горизонту

6. Як змінюватиметься горизонтальна складова швидкості підчас льоту тіла?

7. Як змінюватиметься вертикальна складова швидкості? Написати рівняння для вертикальної складової.

8. Чому дорівнює вертикальна складова швидкості в найвищій точці льоту тіла?

IV. Обертальний рух

38.Поняття про обертальний рух.

З а приклади обертального руху можуть бути: обертання Землі навколо осі, обертання різних частин машин — маховиків, шківів та багатьох інших деталей машин.

Обертальним рухом називається такий рух, при якому всі точки тіла рухаються по колах, центри яких містяться на одній прямій лінії, що її називають віссю.

Розглянемо рух окремої точки на ободі маховика (рис. 29).

Швидкість, з якою рухається точка по дузі кола, називається лінійною швидкістю цієї точки.

В она вимірюється довжиною дуги (рис. 30), пройденої за одиницю часу.

Лінійну швидкість точки можна обчислити, знаючи число обертів маховика за одну секунду і радіус.

Приклад. Маховик робить обертів за секунду, радіус його дорівнює 1,5 м. Обчислити лінійну швидкість точки , що лежить на ободі маховика.

Розв'язання. Обчислимо довжину кола, тобто той шлях, який зробить точка за один оберт маховика. Дов­жина кола дорівнює , а в нашому прикладі: . За одну секунду маховик робить обертів, значить, шукана лінійна швидкість дорівнює:

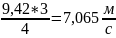
Розв'яжемо задачу в загальному вигляді. Для цього позначимо радіус маховика, як і раніше, буквою 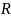, число оборотів за секунду буквою лінійну швидкість точки , що рухається рівномірно по колі, буквою . Тоді маємо: тобто лінійна швидкість точки обертального тіла прямо пропорційна до радіуса і числа обертів за одну секунду.

Запитання та вправи

1. Який рух називається обертальним ?

2. Що таке лінійна швидкість ?

3. Визначити лінійну швидкість точки, що знаходиться на ободі маховика з діаметром на 2 м, який робить 40 обертів на хвилину.