Р Дано: , ешение:

Обозначим узлы А и В. Произвольно укажем направление токов на каждом из участков цепи. Для узла А запишем первое правило Кирхгофа: .

В ыделим в разветвленной цепи простые контуры I и II . Зададим направление их обхода. Запишем для контуров второе правило Кирхгофа: Подставим числовые значения сопротивлений и ЭДС и получим систему уравнений:

Составим определители:

Следовательно,

Ответ:

Примечание: если при решении системы уравнений ток получился отрицательным, это означает, что в цепи он течет в противоположном направлении.

17.7. Работа и мощность постоянного тока. Закон Джоуля – Ленца

Рассмотрим произвольный участок цепи постоянного тока, к концам которого приложено напряжение U. За время t через каждое сечение проводника проходит заряд . При этом силы электростатического поля и сторонние силы совершают работу

В случае, когда проводник неподвижен и химических превращений в нём не происходит, работа тока затрачивается на увеличение внутренней энергии проводника, в результате чего проводник нагревается. Таким образом, при протекании тока в проводнике выделяется количество теплоты

(17.7.1)

Это соотношение было установлено экспериментально и носит название закона Джоуля – Ленца.

Если сила тока меняется со временем, то количество теплоты вычисляется по формуле:

(17.7.2)

Разделив работу A на время, за которое она совершается, найдём мощность, развиваемую током на рассматриваемом участке цепи:

(17.7.3)

В системе СИ единицей электрической мощности является

Пример 17.7.1. Сила тока в проводнике сопротивлением равномерно возрастает от до за время . Определить количество теплоты, выделившегося в проводнике за это время.

Р Дано: ешение.

Согласно закону Джоуля - Ленца для бесконечного малого промежутка времени, .

П о условию задачи сила тока равномерно растёт, то есть , где – коэффициент пропорциональности. Очевидно, что . Следовательно, , откуда .

Вычисляя, получим

О твет: 600 Дж.

17.8. Коэффициент полезного действия источника тока

Рассмотрим практически важный вопрос об использовании энергии источника тока.

Пусть источник тока с э.д.с. и внутренним сопротивлением r замкнут на внешнюю цепь (нагрузку) с сопротивлением R (рис. 17.8.1). Выясним, каким должно быть сопротивление нагрузки R для того, чтобы получить в цепи максимальную силу тока, максимальную полезную мощность и максимальный коэффициент полезного действия. Дадим определение перечисленным выше величинам.

Полезной мощностью называется мощность, выделяющаяся на нагрузке

(17.8.1)

Ток в цепи определяется законом Ома: ,

Поэтому

. (17.8.2)

Когда источник работает на внешнюю цепь, то ток протекает также и внутри источника, поэтому некоторая мощность тратится на выделение тепла внутри источника. Следовательно, полная мощность источника тока

(17.8.3)

Коэффициент полезного действия источника тока определяется как отношение полезной мощности к полной

(17.8.4)

и зависит от сопротивления нагрузки.

1. Чтобы найти максимальную полезную мощность, возможную при данном источнике, необходимо продифференцировать выражение 17.8.3 по сопротивлению и приравнять производную к нулю. Решив полученное уравнение, найдем, что .

Следовательно, полезная мощность достигает наибольшего значения, если

сопротивление внешней цепи (нагрузки) равно внутреннему сопротивлению источника тока. Ток в цепи при этом , то есть равен половине тока короткого

замыкания, а наибольшее возможное значение полезной мощности .

П ри (рис. 17.8.2).

2. Полная мощность Р и сила тока I отличаются лишь постоянным множителем , поэтому их зависимость от сопротивления одинакова (рис. 17.8.2).

При (короткое замыкание), Тогда

П ри , и .

3. Коэффициент полезного действия источника тока равен 0 при и 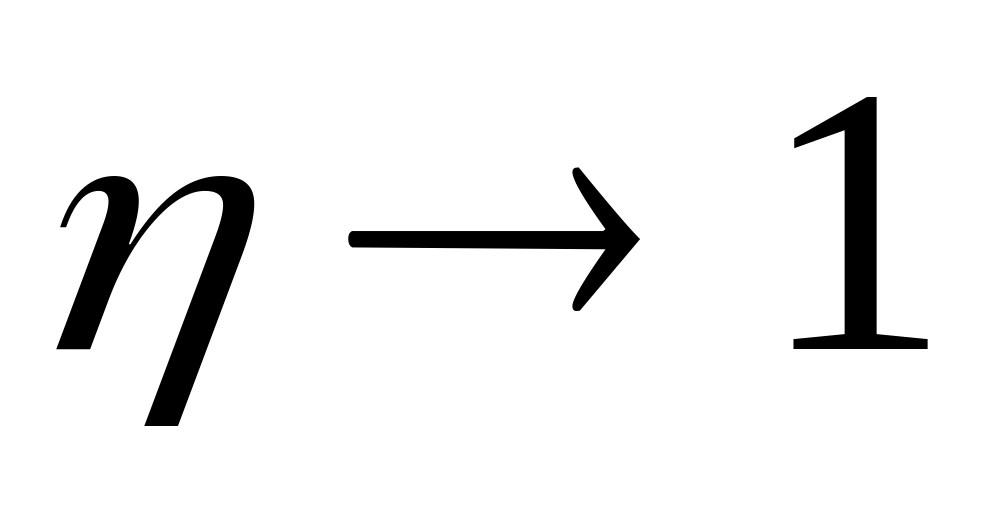при (рис. 17.8.3). При , .

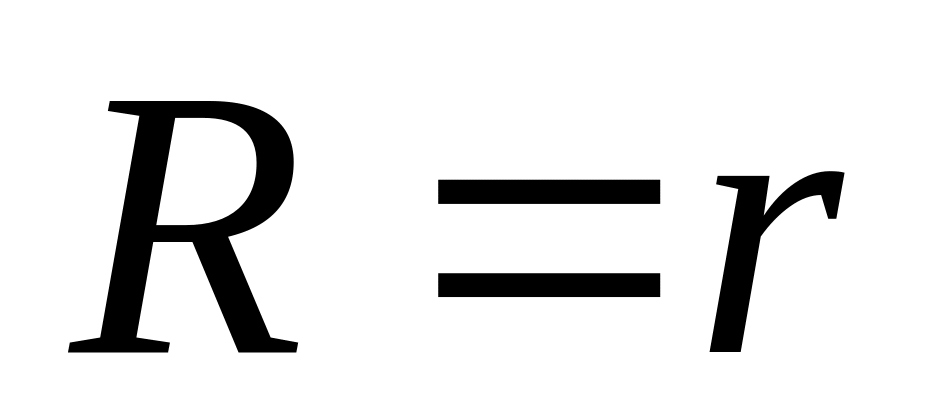Таким образом, требования получения максимального тока в цепи, максимальной полезной мощности и максимального к.п.д. противоречивы. Для получения возможно большего тока сопротивление нагрузки должно быть малым по сравнению с внутренним сопротивлением источника, но при этом близки к нулю полезная мощность и к.п.д.: почти вся совершаемая источником тока работа идёт на выделение тепла на внутреннем сопротивлении. Для того, чтобы получить для данного источника максимальную полезную мощность, следует взять нагрузку , но в этом случае . Любую полезную мощность Р₁ можно получить при двух значениях сопротивления нагрузки R₁ и R₂. На практике для получения заданной полезной мощности следует выбрать нагрузку с большим сопротивлением R₂, так как при этом выше.

Рассмотрим, как указанные величины зависят от силы тока в цепи.

1. Полезную мощность представим в виде:

(17.8.4)

Она обращается в нуль, если и (рис. 17.8.4).

Первое решение соответствует разомкнутой цепи , второе – короткому замыканию .

М аксимум полезной мощности найдём, продифференцировав выражение 17.8.4 по силе тока и приравняв производную к нулю:

2. Полная мощность линейно вырастает с ростом силы тока (рис. 17.8.4).

3. З ависимость к.п.д. от силы тока имеет вид: (рис. 17.8.5). Если , то (цепь разомкнута). Если , то (короткое замыкание - полезной мощности нет, а мощность развиваемая источником, полностью расходуется внутри него).

Пример 17.8.1. Определить внутреннее сопротивление источника тока, если во внешней цепи при силе тока , развивается мощность , а при силе тока , развивается мощность .