Р Дано: . Ешение:

Е мкость при последовательном соединении конденсаторов:

, , т.е., . Емкость при параллельном соединении конденсаторов ; . Отношение емкостей ,

Ответ: при параллельном соединении емкость больше в 25 раз.

16.5. Энергия уединенного проводника

Любой заряженный проводник можно рассматривать как систему точечных зарядов, распределенных по поверхности проводника. Потенциал всех точек заряженного проводника одинаков: . Поэтому

. (16.5.1)

16.6. Энергия заряженного конденсатора

Пусть потенциал обкладки, на которой находится заряд , равен , а потенциал обкладки, на которой находится заряд , равен . Тогда каждый из элементарных зарядов, на которые можно разделить , находятся в точке с потенциалом , а каждый из зарядов, на которые можно разделить заряд , находятся в точке с потенциалом . Энергия такой системы равна:

. (16.6.1)

С учетом того, что , энергия конденсатора равна:

. (16.6.2)

Пример 16.6.1. Плоский парафиновый (диэлектрическая проницаемость парафина ) конденсатор с площадью пластин подключен к батарее, э.д.с. которой . Определить работу внешних сил по раздвижению пластин от до , если 1) пластины от батареи отключали; 2) пластины от батареи не отключали.

Р Дано: , , , ешение:

1 . Система изолирована – справедлив закон сохранения энергии. Работа внешних сил равна изменению энергии системы , где энергия поля конденсатора в конечном состоянии (пластины находятся на расстоянии ), энергия поля конденсатора в начальном состоянии (пластины находятся на расстоянии ), .

Выразим энергию через заряд на пластинах, т.к. заряд пластин, отключенных от источника при их раздвижении, не изменяется:

и . Отсюда .

Так как , а , то

2. При включенной батарее (система не является изолированной) заряд с пластин будет перемещаться к клеммам батареи. При этом разность потенциалов остается неизменной . С увеличением d емкость будет убывать, следовательно, будет убывать заряд и напряженность поля . Так как величины напряженности поля и заряда, необходимые для определения работы, изменяются, то для вычисления работы необходимо провести интегрирование: , где элементарная работа. , где напряженность поля, создаваемого зарядом одной пластины.

Выразим напряженность и заряд через переменную величину x, выражающую расстояние между пластинами: , или .С учетом этого

и

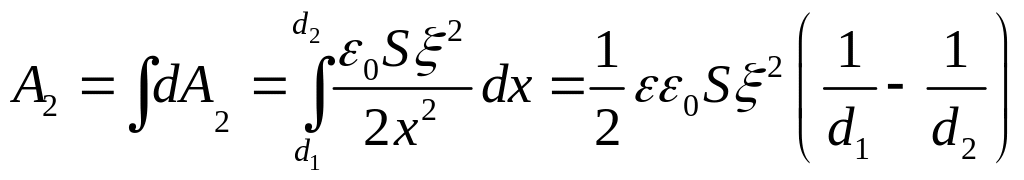
О твет:

16.7. Объемная плотность энергии электростатического поля

Рассмотрим плоский конденсатор, между обкладками которого поле однородно.

Энергию заряженного конденсатора представим через величины, характеризующие поле между его обкладками:

. (16.7.1)

Введем понятие объемной плотности энергии электростатического поля как отношения энергии поля к объему, в котором она локализована

, (16.7.2)

С учетом, что , получим

. (16.7.3)

Формула получена для однородного поля. Но ею можно воспользоваться для подсчета полной энергии электрического поля и в случае, когда поле неоднородно.

Например, в пространстве вокруг заряженного тела напряженность электрического поля уменьшается по мере удаления от тела. В любом месте пространства всегда возможно выбрать такой небольшой объем , что напряженность поля в нем практически не изменяется. Тогда в выбранном объеме заключена энергия

.

Если теперь весь объем, где имеется электрическое поле, разбить на элементарные объемы, подсчитать энергию каждого из них, а затем все просуммировать, то мы получим полную энергию электрического поля:

. (16.7.4)

П ример 16.7.1. Металлический шар радиусом несет заряд . Шар окружен слоем парафина толщиной . Определить энергию электрического поля, заключенного в слое диэлектрика.