Р Дано: , , , , , , ешение:

По принципу суперпозиции полей напряженность поля в любой точке . Внутри каждой сферы . Следовательно, в интервале , которому пренадлежит точка , поле отсутствует: . Графиком зависимости на участке (рис. 14.2.14) будет прямая, совпадающая с осью Ох.

В точке напряженность поля второй сферы и . Численное значение В интервале напряженность поля убывает обратно пропорционально . Началу кривой соответствует , концу кривой соответствует (рис. 14.2.14).

В точке напряженность , и ее численное значение В интервале напряженность убывает обратно пропорционально . Началу кривой соответствует , при (рис. 14.2.14).

О твет: , , .

VI. Поле объемно заряженного шара.

Поле шара обладает сферической симметрией. Окружим шар радиуса R сферической поверхностью S₁ радиуса . Тогда этот случай не будет отличаться от рассмотренного ранее случая заряженной сферической поверхности: снаружи шара поле такое же, как если бы весь заряд был сосредоточен в его центре

(14.2.18)

Д ля расчета поля внутри шара применим теорему Гаусса к сферической поверхности S₂ радиуса (рис. 14.2.15):

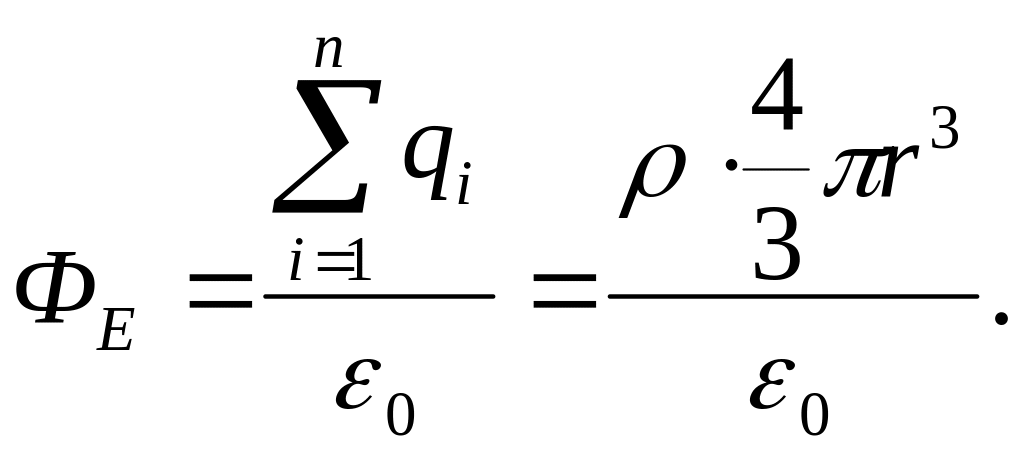
где объемная плотность заряда.

С другой стороны .

В силу симметрии напряженность электрического поля на сферической поверхности одинакова и имеет только нормальную составляющую, следовательно, . После интегрирования получим . Поскольку , то

…………(14.2.19)

Таким образом, напряженность поля заряженного шара

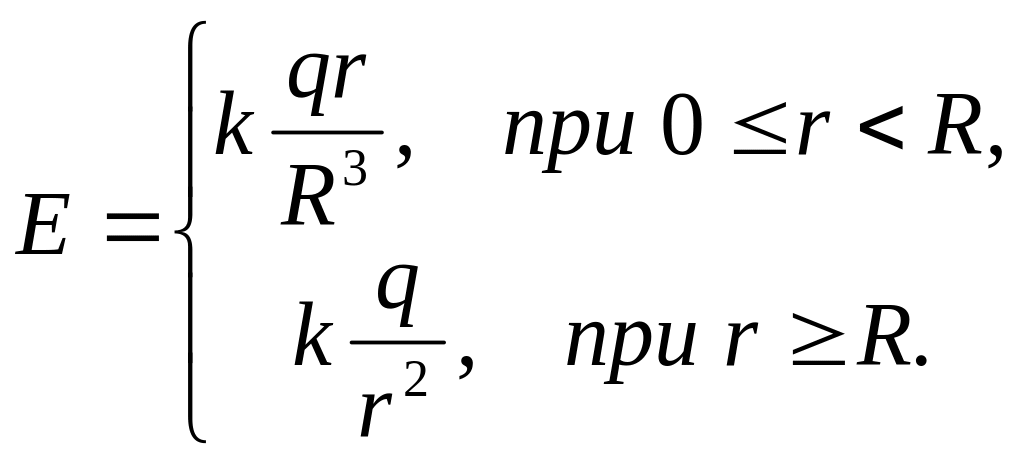(14.2.20)

Зависимость напряженности электрического поля объемно заряженного шара от расстояния до центра шара изображена на рис. 14.2.16.

Разность потенциалов между точками 1 и 2 внутри шара (рис. 14.2.17)

.

Разность потенциалов между точками 3 и 4 вне шара (рис. 14.7.6)

.

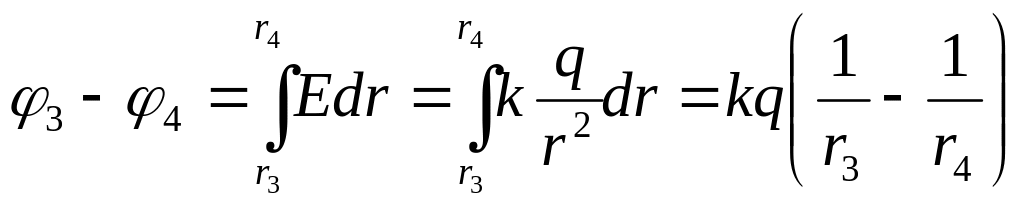
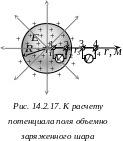Таким образом, если , то потенциал равномерно заряженного шара

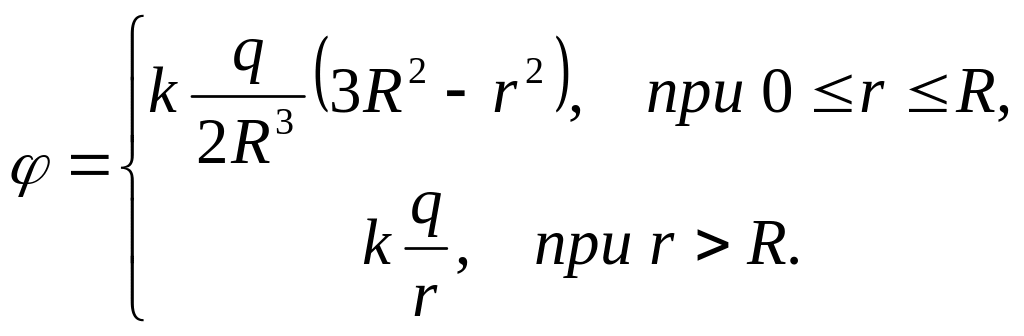(14.2.21)

На рис. 14.2.16 показан график зависимости потенциала от расстояния до центра шара.

П ример 14.2.6. Сплошной шар радиусом несет заряд, равномерно распределенный с объемной плотностью . Определить напряженность Е электрического поля в точках: 1) на расстоянии от центра сферы; 2) на поверхности сферы; 3) на расстоянии от центра сферы. Построить график зависимости .

Р Дано: , , , , ешение:

Поле внутри и на поверхности шара найдем по формуле 14.2.19:

График зависимости на отрезке носит линейный характер, так как прямо пропорциональна r (рис. 14.2.17).

Поле за пределами шара по формуле 14.2.20 равно:

График зависимости (рис. 14.2.17) на отрезке носит нелинейный характер, так как Е обратно пропорциональна

Потенциал внутри шара 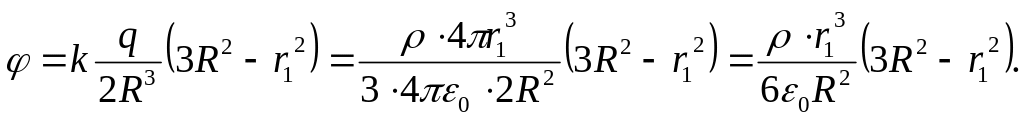Его численное значение

О твет: , , .

Глава 15. Электростатическое поле в диэлектриках

_{Электрическое поле вызывает изменения в веществе, внесенном в это поле. Чтобы понять, почему это происходит, рассмотрим действие электрического поля на простейшую систему зарядов – электрический диполь.}