Р Дано: , ешение:

П о формуле 14.1.1 .

Ответ: .

Пример 14.1.2. Дана система точечных зарядов в вакууме и замкнутые поверхности S_1, S₂ и S₃ (рис. 14.1.4). Определить, чему равен поток вектора напряженности электростатического поля через каждую из поверхностей.

Решение:

Так как внутри поверхности S₁ находится только заряд 2q, то поток вектора напряженности . Внутри поверхности S₂ находятся заряды 2q и -2q, следовательно, . Внутри поверхности S₃ находятся заряды 2q, -2q и q, следовательно, .

О твет: , , .

14.2. Применение теоремы Гаусса для расчета электрических полей

Теорема Гаусса значительно упрощает процесс вычисления напряженности электрических полей. А установленная в параграфе 13.8 связь между напряженностью поля и потенциалом позволяет по известной напряженности найти разность потенциалов между двумя произвольными точками этого поля.

1. Поле бесконечной однородно заряженной плоскости.

Для определенности считаем, что заряд плоскости положителен и распределен с поверхностной плотностью . Вследствие симметрии распределения заряда вектор напряженности направлен перпендикулярно плоскости (рис. 14.2.1).

В оспользуемся теоремой Гаусса, для чего выберем замкнутую поверхность в виде цилиндра, основания которого площадью S находятся на равном расстоянии от плоскости и параллельны ей. Суммарный заряд внутри

цилиндрической поверхности равен . Следовательно,

.

Р азобьем интеграл по замкнутой цилиндрической поверхности на сумму трех интегралов – по боковой поверхности цилиндра и по поверхности двух оснований (последние два интеграла в силу симметрии равны между собой). Тогда

.

П оток вектора напряженности через боковую поверхность цилиндра равен нулю, так как равна нулю нормальная составляющая напряженности поля на поверхность цилиндра. На поверхности оснований вектор напряженности поля не изменяется , следовательно, напря-женность Е можно вынести за знак интеграла. Поэтому

. Таким образом, , откуда

. (14.2.1)

Напряженность поля не зависит от расстояния до плоскости. Следовательно, поле по обе стороны от плоскости однородно (рис. 14.2.2).

Чтобы найти разность потенциалов между точками, лежащими на расстояниях r₁ и r₂ от плоскости (рис. 14.2.3), воспользуемся формулой (13.7.1) интегральной связи

между напряженностью и потенциалом

. (14.2.2)

Полагая потенциал плоскости равным нулю, получаем

(14.2.3)

Соответственно, график зависимости потенциала бесконечной плоскости от расстояния будет линейной функцией (рис 14.2.2).

П ример 14.2.1. Разность потенциалов точек, отстоящих от заряженной плоскости на расстоянии и , равна Чему равен заряд и напряженность плоскости в вакууме, если ее площадь ?

Р Дано: , , , ешение:

Р азность потенциалов точек электрического поля, созданного заряженной плоскостью, , где . Напряженность плоскости , или . Заряд плоскости

Ответ: , .

Поле двух параллельных бесконечных однородно заряженных плоскостей (поле плоского конденсатора).

По принципу суперпозиции полей в любой точке поля . Для плоского конденсатора

, следовательно, . Направление векторов и указано на рис. 14.2.4.

Напряженность поля нужно вычислять для трех областей:

, , .

Учитывая значения и , получим и . Таким образом, поле сосредоточе-

но между обкладками конденсатора. Зависимость напряженности поля плоского конденсатора от расстояния r до положительной обкладки равна

(14.2.4)

и представлена на рис. 14.2.5.

Разность потенциалов между точками, лежащими на расстояниях r₁ и r₂ от положительно заряженной плоскости (рис. 14.2.6), равна

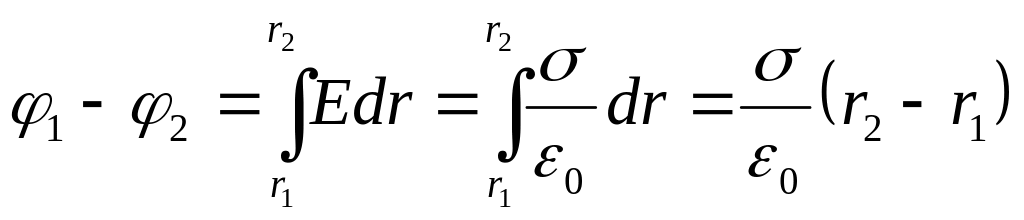. (14.2.5)

Соответственно, зависимость потенциала электрического поля конденсатора от расстояния от положительно заряженной пластины, полагая равна

(14.2.6)

и представлена на рис. 14.2.5.

Напряжение между плоскостями, образующими конденсатор (обкладками)

, (14.2.7)

где расстояние между обкладками .

П ример 14.2.2. Электростатическое поле создается двумя бесконечными плоскостями, заряженными равномерно разноименными зарядами с поверхностной плотностью и . Расстояние между плоскостями . Определить напряженность электростатического поля: 1) между плоскостями; 2) за пределами плоскостей. Построить графики зависимости и .