2.2. Основные величины динамики

Инертность - свойство, которое проявляется в И.С.О. и состоит в изменении скорости тела под действием внешних сил, т.е. в появлении ускорений.

Чем больше масса, тем большую силу нужно приложить, чтобы сдвинуть тело или остановить его движение.

Инерция - свойство тела в инерциальных системах сохранять скорость своего движения неизменной при отсутствии внешних воздействий.

Например, пассажиры при резком торможении автобуса движутся по инерции в прежнем направлении.

Основные величины динамики:

1. Масса m - является мерой инертности тела. Размерность массы: [m] = кг.

2. Момент инерции тела J – скалярная величина, равная сумме произведений масс материальных точек на квадраты расстояний от них до некоторой оси:

(2.7)

Размерность момента инерции:

3. Импульс – векторная величина, равная произведению массы тела на вектор скорости:

(2.8)

В классической механике скорость тела считается малой по сравнению со скоростью света.

Размерность импульса: [p] = м/с.

Если рассматривать совокупность материальных точек движущихся со скоростями , то полный импульс системы

(2.9)

4. Момент импульса L ‑ векторная величина, равная векторному произведению радиус-вектора r на импульс p:

(2.10)

Размерность момента импульса:

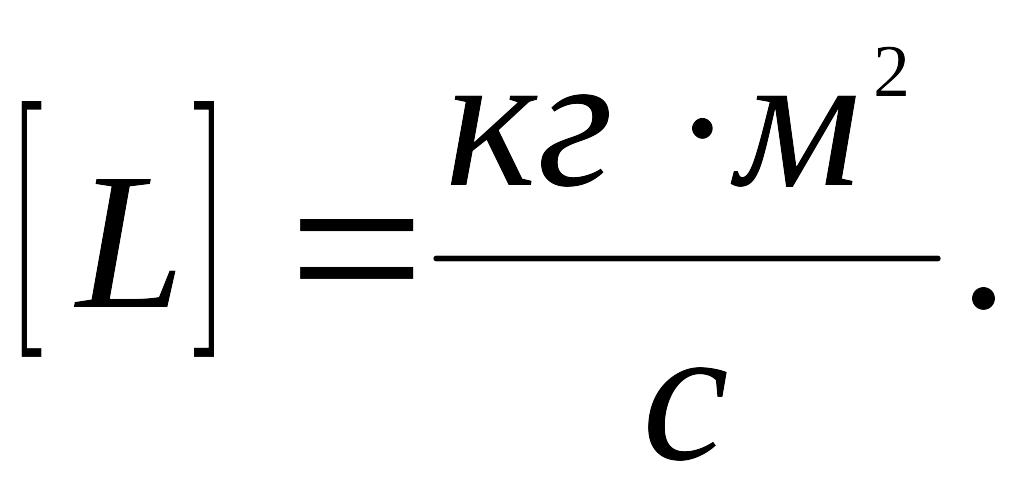
5. Сила F - величина, характеризующая степень воздействия внешних тел на данное тело, приводящего к изменению скорости или направления движения.

Размерность силы: (Ньютон).

6. Момент силы – векторная величина, равная векторному произведению радиус-вектора r на силу F:

. (2.11)

Размерность момента силы:

Момент инерции, момент импульса и момент силы являются вращательными аналогами массы, импульса и силы, соответственно, и применяются для описания вращательного движения.

2.3. Законы Ньютона

И. Ньютон обобщил известные к тому времени достижения механики и создал систему законов движения материальной точки и абсолютно твердого тела.

И

18

саак Ньютон (1642 - 1727), выдающийся английский ученый, создатель классической физики. Окончил Кембриджский университет. Работы относятся к механике, оптике, астрономии, математике. Ньютон сформулировал основные законы классической механики, открыл закон всемирного тяготения. Он открыл дисперсию света и развил корпускулярную теорию света.

Л

18

юбое тело макроскопических размеров всегда можно рассматривать как совокупность материальных точек и, следовательно, достаточно точно описать его движение. В современной физике под классической механикой понимают механику материальной точки, системы материальных точек и механику абсолютно твердого тела.

В основе классической механики лежат три закона:

Закон 1. Всякое тело находится в состоянии покоя или прямолинейного равномерного движения, пока воздействие со стороны других тел не заставит его изменить это состояние.

Закон 2. Скорость изменения импульса тела равна действующей на тело силе F.

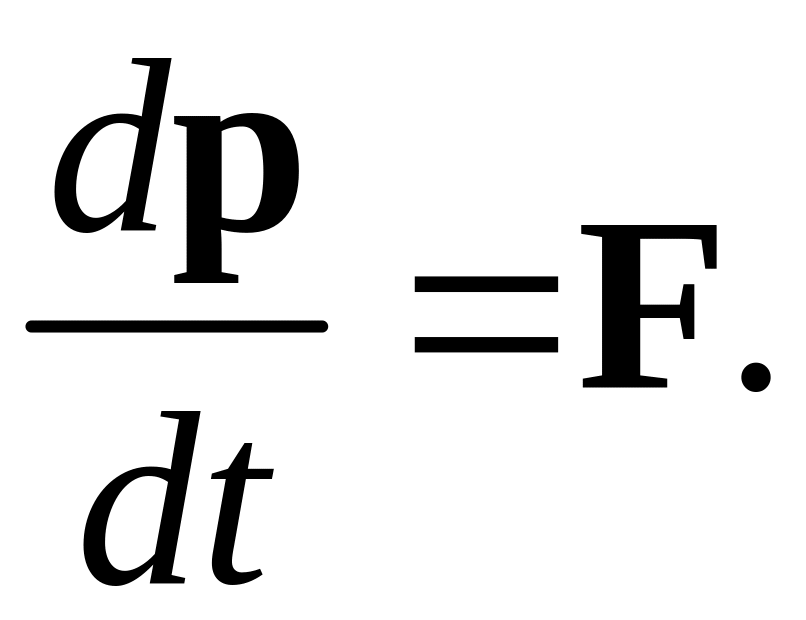(2.12)

Закон 3. Силы, с которыми действуют друг на друга взаимодействующие тела, равны по величине и противоположны по направлению:

(2.13)

Первый закон называется законом инерции и открыт Г. Галилеем. Галилей впервые показал, что «степень скорости, обнаруживаемая телом, нерушимо лежит в самой его природе, в то время как причины ускорения или замедления являются внешними». Движение тела может происходить без воздействия внешних сил - по инерции, но трение мешает это увидеть.

Формулировка второго закона, в которой используется понятие импульса, является наиболее общей, что позволяет учесть возможное изменение массы во время движения (например, при движении тележки с песком под дождем).

Если при движении масса тела не изменяется, то получим знакомое выражение для закона Ньютона:

(2.14)

У

20

скорения тел определяются вторым законом Ньютона. По заданным начальным значениям координат и скоростей всех частиц системы в начальный момент времени можно найти эти величины в любой последующий момент времени.

Третий закон выполняется при контактных взаимодействиях, а также при взаимодействии покоящихся тел, находящихся на некотором расстоянии друг от друга.

Законы Ньютона выполняются только в системах отсчета, движущихся без ускорения, т.е. в инерциальных системах отсчета.

Примером системы, в которой не выполняются законы Ньютона, является система отсчета, связанная с самолетом, быстро набирающим скорость при взлете. Сила инерции, возникающая при ускорении, не перемещает пассажиров, т.к. со стороны спинки действует сила, противоположная по направлению. В самолете, движущемся без ускорения, сила инерции не возникает, и авиапассажиры могут находиться в состоянии покоя или равномерного движения относительно И.С.О., не находясь в креслах.

Уравнения динамики не изменяются при переходе от одной И.С.О. к другой, поэтому нельзя утверждать, движется ли данная система прямолинейно и равномерно или покоится. Это следует из второго закона Ньютона и равенства ускорений при переходе из одной инерциальной системы в другую. Отсюда следует т.е. все законы имеют одинаковый вид в различных И.С.О.