
- •Предисловие
- •Введение
- •Глава 1. Кинематика материальной точки и твердого тела
- •1.1. Кинематика поступательного движения материальной точки и твердого тела
- •1.2. Кинематика вращательного движения материальной точки
- •Контрольные вопросы:
- •Глава 2. Динамика материальной точки и поступательного движения твёрдого тела
- •2.1. Принцип относительности Галилея
- •2.2. Основные величины динамики
- •2.3. Законы Ньютона
- •Глава 3. Законы сохранения энергии и импульса
- •3.1. Сохраняющиеся величины
- •3.2. Работа. Мощность. Коэффициент полезного действия
- •3.3. Понятие поля. Консервативные силы. Потенциальная энергия
- •Пример 1.
- •Пример 2.
- •3.4. Кинетическая энергия
- •3.5. Закон сохранения механической энергии системы невзаимодействующих частиц
- •3.6. Закон сохранения полной механической энергии
- •3.7. Закон сохранения импульса
- •3.8. Применение законов сохранения энергии и импульса
- •Неупругий удар
- •Упругий удар
- •Явление отдачи при вылете снаряда из орудия
- •Контрольные вопросы:
- •Глава 4. Силы в природе
- •4.1. Взаимодействие в природе. Закон всемирного тяготения
- •4.2. Сила тяжести. Вес тела. Невесомость
- •Движение тела под действием силы тяжести
- •1. Движение тела вверх:
- •2. Движение тела вниз:
- •Движение тела по горизонтали:
- •4.3. Упругие силы
- •4.4. Силы трения
- •Трение покоя
- •Контрольные вопросы:
- •Глава 5. Динамика твердого тела
- •5.1. Движение твердого тела
- •5.2. Степени свободы
- •5.3. Центр масс
- •5.4. Момент импульса
- •5.5. Главные моменты инерции
- •Теорема Гюйгенса – Штейнера
- •5.6. Момент силы
- •5.7. Кинетическая энергия вращающегося твердого тела
- •Глава 6. Закон сохранения момента импульса
- •6.1. Закон сохранения момента импульса
- •6.2. Условие сохранения момента импульса относительно оси для незамкнутой системы
- •6.3. Закон сохранения момента импульса для вращающейся системы тел
- •6.4. Применение закона сохранения момента импульса
- •Контрольные вопросы:
- •Глава 7. Колебательное движение
- •7.1. Классификация колебательного движения
- •7.2. Гармонические колебания
- •7.3. Математический маятник
- •7.4. Физический маятник
- •7.5. Сложение колебаний Сложение одинаково направленных колебаний
- •Сложение взаимно перпендикулярных колебаний
- •7.6. Затухающие колебания
- •7.7. Вынужденные колебания
- •Контрольные вопросы:
- •Глава 8. Молекулярная физика
- •8.1. Основные положения молекулярно-кинетической теории
- •Основные величины, характеризующие массу, размер и число молекул в веществе:
- •8.2. Уравнение состояния идеального газа
- •Уравнение состояния идеального газа
- •8.3. Основное уравнение молекулярно-кинетической теории
- •Основное уравнение мкт:
- •8.4. Взаимодействие молекул
- •8.5. Реальные газы. Уравнение Ван-дер-Ваальса Фазовые равновесия и переходы
- •8.6. Характеристики жидкого состояния
- •5. Жидкости с водородными связями (h2o);
- •Свойства жидкостей:
- •Контрольные вопросы:
- •Глава 9. Равновесная термодинамика
- •9.1. Внутренняя энергия
- •9.2. Работа. Количество теплоты
- •9.3. Термодинамические системы
- •9.4. Первое начало термодинамики
- •9.4. Первое начало термодинамики
- •9.5. Второе и третье начало термодинамики
- •Второе начало термодинамики
- •Третье начало термодинамики
- •9.6. Теплоёмкость идеального газа
- •9.7. Применение первого начала термодинамики для вывода уравнения адиабатного процесса
- •Уравнение адиабатного процесса в параметрах t,V:
- •9.8. Работа, совершаемая газом при различных процессах
- •9.9. Графическое изображение термодинамических процессов
- •9.10. Применение законов термодинамики для расчета круговых процессов
- •К. П. Д. Идеальной тепловой машины Карно
- •Теорема Карно:
- •Контрольные вопросы:
- •Глава 10. Элементы статистической физики
- •10.1. Статистический вес
- •10.2. Энтропия
- •10.3. Распределение Гиббса
- •10.4. Распределение молекул по скоростям Максвелла
- •10.5. Распределение Больцмана молекул в потенциальном поле. Барометрическая формула
- •Контрольные вопросы:
- •Глава 11. Электростатическое поле
- •11.1. Закон сохранения заряда
- •11.2. Взаимодействие зарядов. Закон Кулона
- •Закон Кулона
- •Принцип суперпозиции сил
- •11.3. Напряженность электрического поля
- •Принцип суперпозиции напряженностей
- •Контрольные вопросы:
- •Глава 12. Теорема остроградского-гаусса для электростатического поля
- •12.1. Теорема Остроградского-Гаусса для электростатического поля в вакууме
- •12.2. Применение теоремы Остроградского - Гаусса для расчета электростатического поля равномерно заряженного сферического проводника
- •12.3. Применение теоремы Остроградского - Гаусса для расчета электростатического поля бесконечной заряженной плоскости
- •12.4. Применение теоремы Остроградского - Гаусса для расчета электростатического поля бесконечного заряженного цилиндра
- •Г 153 лава 13. Работа электрического поля. Потенциал.
- •13.1. Работа электрического поля по перемещению заряда
- •13.2. Потенциальная энергия взаимодействия зарядов
- •13.3. Электрический потенциал
- •13.4. Потенциал заряженной сферы, плоскости, цилиндра
- •Потенциал электрического поля заряженной плоскости:
- •Потенциал электрического поля заряженного цилиндра:
- •Глава 14. Диэлектрики в электростатическом поле
- •14.1. Проводники и диэлектрики
- •14.2. Типы диэлектриков
- •14.3. Поляризация диэлектриков
- •14.4. Напряженность электрического поля и электрическое смещение
- •Контрольные вопросы:
- •Глава 15. Проводники в электростатическом поле
- •15.1. Распределение зарядов в проводниках
- •15.2. Электроемкость проводников
- •Электроемкость сферического проводника
- •15.3. Конденсаторы
- •Электроемкость плоского конденсатора
- •15.4. Энергия заряженных проводников и конденсаторов. Энергия электрического поля
- •Глава 16. Постоянный ток закон ома
- •16.1. Электрический ток
- •16.2. Разность потенциалов, напряжение и электродвижущая сила
- •16.3. Закон Ома. Сопротивление проводников
- •16.4. Закон Ома для участка цепи и замкнутой цепи. Закон Ома для плотности тока
- •Контрольные вопросы:
- •Глава 17. Работа электрического тока. Мощность. Закон джоуля – ленца
- •17.1. Работа электрического тока
- •17.2. Мощность электрического тока
- •17.3. Закон Джоуля - Ленца для участка цепи
- •17.4. Применение закона Джоуля – Ленца
- •Контрольные вопросы:
- •Глава 18. Релятивистская кинематика
- •18.1. Теория относительности Эйнштейна
- •Преобразования Лоренца для координат и времени
- •18.2. Следствия из преобразований Лоренца
- •18.3. Интервал между двумя событиями. Абсолютность интервала
- •18.4. Преобразование скоростей
- •Глава 19. Релятивисткая динамика
- •19.1. Принцип наименьшего действия Гамильтона
- •19.2. Импульс частицы
- •19.3. Сила
- •19.4. Энергия
- •19.5. Связь между энергией и импульсом
- •19.6. Четырехмерные векторы
- •19.7. Законы сохранения в релятивистской механике
- •Список литературы
- •Содержание предисловие 3 введение 4
- •Список литературы 215
13.2. Потенциальная энергия взаимодействия зарядов
Для потенциального поля справедливо соотношение между силой F и потенциальной энергией:
![]() (13.10)
(13.10)
Найдем потенциальную энергию точечного заряда q' в поле другого точечного заряда q:
 (13.11)
(13.11)
Эта энергия определяется с точностью до константы C, выбор которой может быть сделан произвольно. Энергию W можно рассматривать как потенциальную энергию взаимодействия точечных зарядов q и q'. Единица измерения энергии [W] = Дж.
Работа, совершаемая силами электростатического поля, равна разности потенциальной энергии взаимодействия зарядов q' и q в точках 1 и 2:
 (13.12)
(13.12)
Выберем
точку отсчета, в которой W
= 0. Так, если при r
![]() W
®
0, то отсюда следует, что C
= 0.
W
®
0, то отсюда следует, что C
= 0.
13.3. Электрический потенциал
Потенциал определяется как электрическая потенциальная энергия единичного положительного заряда, помещенного в данную точку поля:
![]() (13.13)
(13.13)
Потенциал поля, создаваемого зарядом q, не зависит от величины пробного заряда q', помещенного в это поле:
 (13.14)
(13.14)
Потенциал, также, как и энергия, определяется неоднозначно и зависит от выбора постоянной C.
Электрический потенциал численно равен работе, которую необходимо совершить, чтобы перенести единичный заряд q' из бесконечности на расстояние r от точечного заряда q.
Пусть
при
![]() ,
тогда положим С
= 0.
,
тогда положим С
= 0.
Потенциал точечного заряда будет иметь вид:
 (13.15)
(13.15)
На рис. 13.2 показана зависимость потенциала точечного заряда от расстояния r до заряда. Единица измерения потенциала
Вольт, [] = В, 1В = 1Дж/1Кл.

Рис. 13.2.
Напряжением U называется разность потенциалов между двумя точками, численно равная работе, которую необходимо затратить для перемещения единичного заряда из точки 1 в точку 2:
![]() (13.16)
(13.16)
Е
166
Вольта Алессандро (1745 – 1827), итальянский физик, химик и физиолог, родился в Комо. Учился в школе ордена иезуитов. Сконструировал первый источник электрического тока – вольтов столб. Открыл взаимную электризацию разнородных металлов при их контакте. Построил электроскоп, конденсатор.

Рис. 13.3.
Е
157![]() .
.

Рис. 13.4.
На
рис. 13.3 изображены силовые линии
положительного точечного заряда и
перпендикулярные к ним эквипотенциальные
сферические поверхности с потенциалами
![]() ,
,
![]() .
На рис. 13.4 изображены силовые линии и
эквипотенциальные поверхности
электрического поля, создаваемого двумя
разноименно заряженными плоскостями.
.
На рис. 13.4 изображены силовые линии и
эквипотенциальные поверхности
электрического поля, создаваемого двумя
разноименно заряженными плоскостями.
Поверхность заряженного проводника имеет одинаковый потенциал во всех его точках, поэтому эквипотенциальные поверхности повторяют форму проводника (рис. 13.5).

Рис. 13.5.
Потенциал изменяется от точки к точке пространства. Это изменение можно характеризовать с помощью векторной величины, называемой градиентом потенциала. В декартовой системе координат
![]()
где
![]() - частные производные от потенциала по
координатам x,
y, z;
- частные производные от потенциала по
координатам x,
y, z;
![]() - единичные векторы вдоль осей координат
х,
y,
z.
- единичные векторы вдоль осей координат
х,
y,
z.
Если
потенциал зависит только от одной
координаты, например, от радиуса r, тогда
![]()
Зная распределение потенциала в пространстве, можно определить напряженность электрического поля:
![]() (13.18)
(13.18)
В случае однородного поля напряженность связана с напряжением соотношением:
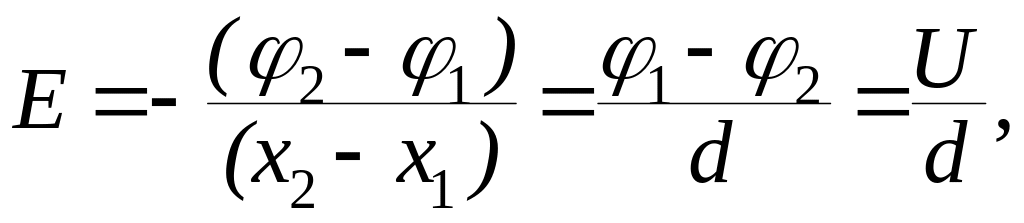 (13.19)
(13.19)
где U – напряжение;
d - расстояние между двумя точками в пространстве.
Электрическое поле между обкладками плоского конденсатора является однородным, также как и поле в проводниках. Если напряженность зависит только от одной координаты x , то связь между напряженностью и потенциалом имеет вид:
![]() (13.20)
(13.20)
Знак минус в формуле указывает, что электрическое поле направлено в сторону уменьшения потенциала.
