Принцип суперпозиции напряженностей

Если имеется несколько заряженных тел с зарядами q₁, q₂, ..., q_n, которые можно считать точечными, то вектор напряженности поля, создаваемого всеми зарядами в некоторой точке, равен сумме векторов напряженностей полей, создаваемых каждым зарядом:

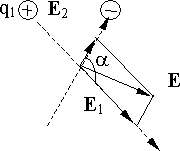
Рис. 11.10.

(11.12)

где 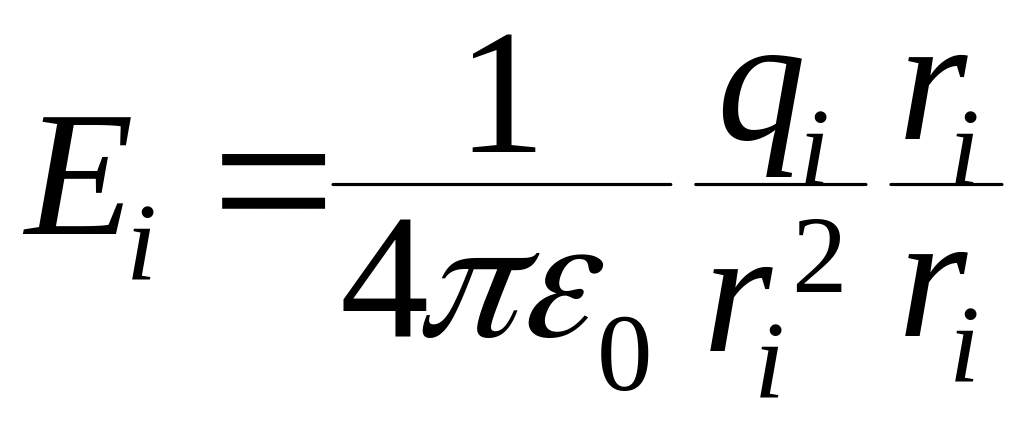- напряженность электрического поля, создаваемого отдельным зарядом.

Для случая двух зарядов:

модуль вектора:

, (11.13)

где  - угол между векторами E₁ и E₂ (рис. 11.10).

Контрольные вопросы:

1. Элементарный заряд. Точечный заряд. Закон сохранения заряда. Закон Кулона.

2. Диэлектрическая проницаемость среды.

3. Линейная, объемная и поверхностная плотность зарядов.

4. Принцип суперпозиции сил.

Глава 12. Теорема остроградского-гаусса для электростатического поля

12.1. Теорема Остроградского-Гаусса для электростатического поля в вакууме

Потоком вектора напряженности электрического поля Е через малый участок поверхности площадью dS называется скалярное произведение вектора напряженности на вектор dS:

(12.1)

где Е – вектор напряженности электрического поля;

dS = dS n – вектор, направленный по нормали n к площадке dS.

Поток вектора Е через поверхность S:

(12.2)

Найдем поток вектора напряженности электрического поля, создаваемого системой точечных зарядов , через замкнутую поверхность:

(12.3)

Полный поток равен алгебраической сумме потоков, создаваемых отдельными зарядами.

В случае непрерывного распределения заряда по поверхности тела принцип суперпозиции не позволяет определить напряженность электрического поля, создаваемого телом. Одним из методов решения задач электростатики является применение теоремы Остроградского - Гаусса.

Поток вектора напряженности электрического поля через любую замкнутую поверхность численно равен алгебраической сумме зарядов, находящихся внутри этой поверхности, умноженной на 4k.

(12.4)

где

Теорему Остроградского – Гаусса запишем в интегральной форме:

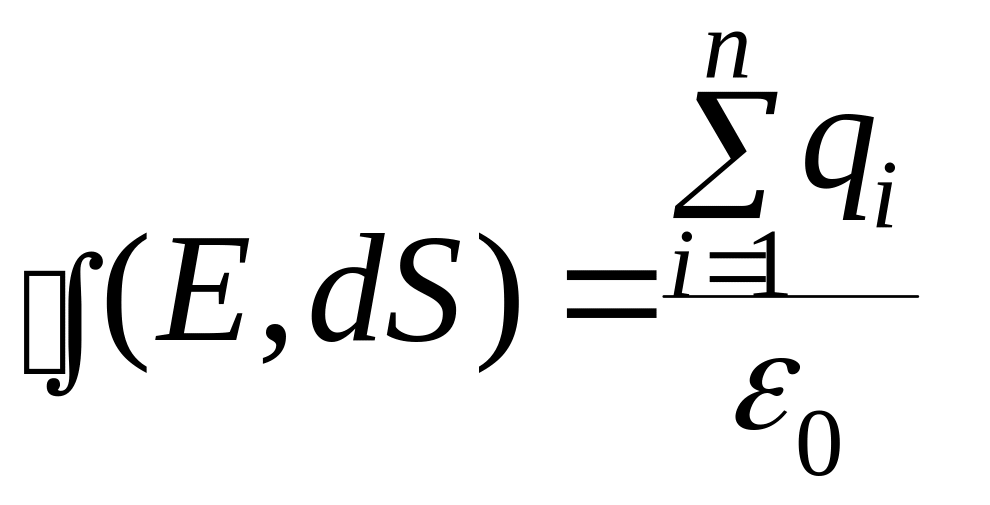(12.5)

Применяя теорему Остроградского – Гаусса, можно рассчитать поле, создаваемое заряженными телами произвольной формы. Если заряды непрерывно распределены по объему, то теорему Остроградского - Гаусса можно написать в виде

(12.6)

или в виде

(12.7)

где  - объемная плотность заряда.

В

157

дифференциальной форме теорема Остроградского – Гаусса:

(12.8)

Остроградский Михаил Васильевич (1801 – 1862), отечественный математик и механик, родился в Пашеновке Полтавской обл. Учился в Харьковском ун-те.

Известны его работы в области математического анализа, математической физики, теоретической механики. Решил ряд задач гидродинамики, теории теплоты, упругости, баллистики. В 1828 г. доказал теорему о преобразовании интегралов.

Гаусс Карл Фридрих (1777 – 1855), немецкий математик, астроном и физик, родился в Брауншвейге. Учился в Геттингенском ун-те. Работы посвящены теории поля, электростатике, магнетизму.

12.2. Применение теоремы Остроградского - Гаусса для расчета электростатического поля равномерно заряженного сферического проводника

Найдем поле сферического проводника радиуса R, на поверхности которого распределен заряд q > 0. Для того чтобы найти напряженность электрического поля E в любой точке на расстоянии r > R от центра, проведем вспомогательную сферическую поверхность радиуса r (рис. 12.1).

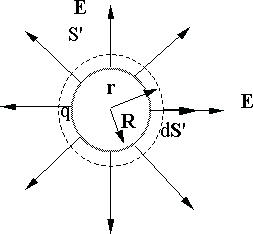
Рис. 12.1.

Найдем поток вектора E через сферу поверхностью . Вектор в любой точке сферической поверхности направлен по внешней нормали к этой поверхности, его направление совпадает с направлением вектора E в любой точке поверхности сферы.

(12.9)

Вследствие симметрии модуль вектора E имеет постоянное значение во всех точках вспомогательной поверхности, поэтому можно вынести E из-под знака интеграла:

(12.10)

Из теоремы Остроградского - Гаусса следует, что , таким образом находим Отсюда следует, что напряженность электрического поля вне сферического проводника:

(12.11)

Напряженность электрического поля в любой точке внутри сферы найдем, проведя вспомогательную сферическую поверхность S' радиусом r < R. Поскольку заряд q распределен по поверхности, то внутри проводника следовательно,

Отсюда следует, что внутри сферы E = 0

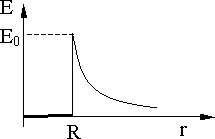
Рис. 12.2.

На рис. 12.2 представлен график зависимости напряженности электрического поля E сферического проводника от расстояния r до центра сферы. Напряженность электрического поля скачком изменяется на границе сферы от E = 0 до и спадает пропорционально вне сферы. Напряженность заряженного шара совпадает с напряженностью сферического проводника, т.е. в проводнике заряд переходит на поверхность и равномерно распределяется по ней. Напряженность поля вне сферического проводника имеет такой же вид, как и напряженность точечного заряда q, помещенного в центр сферы.