Основные величины, характеризующие массу, размер и число молекул в веществе:
1.
Относительная атомная масса:
-
отношение массы атома к одной двенадцатой
части массы атома изотопа углерода
.
Это безразмерная величина, она
характеризует число протонов и нейтронов
в атоме, т.к. масса электрона значительно
меньше массы нуклона.
2.
Относительная молекулярная масса:
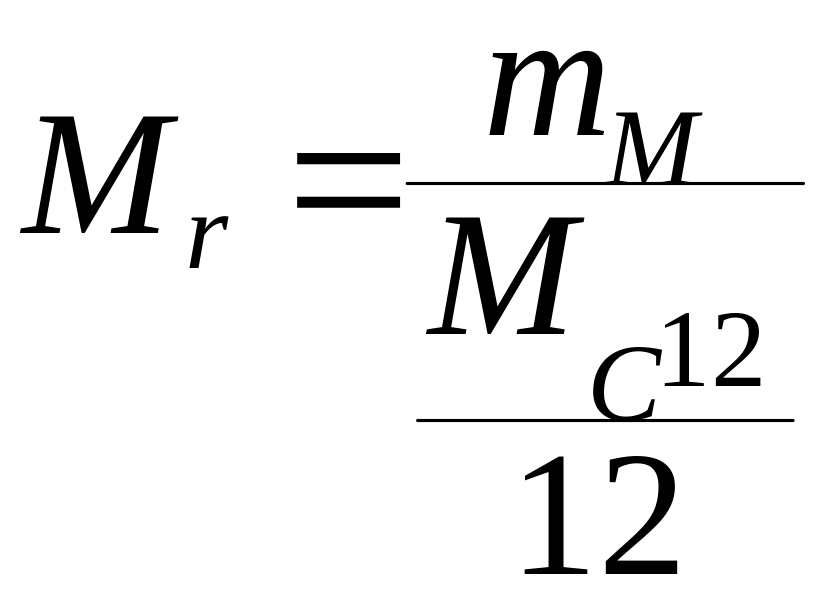- это отношение массы молекулы
к одной двенадцатой части массы изотопа
углерода
.
Относительная молекулярная масса также
является безразмерной величиной.
3.
Относительная
молекулярная масса вещества, состоящего
из нескольких химических элементов:
,
где
-
число атомов i
- го химического элемента;
- относительная атомная масса этого
элемента.
Пример:
Относительная молекулярная масса
углекислого газа
:
.
4.
Число Авогадро
число атомов в двенадцати граммах
изотопа углерода
:
5.
Количество вещества
- это отношение числа атомов или молекул
в веществе к числу Авогадро:
или
.
Размерность количества вещества:
моль. Моль - количество вещества, в
котором содержится число частиц, равное
числу Авогадро.
6.
Молярная масса
- масса моля вещества:
.
Молярная масса численно равна относительной
молекулярной массе, но является размерной
величиной. Размерность молярной массы:
.
7.
Эффективный диаметр молекулы
-
наименьшее расстояние между центрами
молекул при их сближении. Размер молекул
составляет несколько Ангстрем (
).
8.
Концентрация молекул
n
- отношение числа молекул в веществе к
занимаемому объему V:
.
Размерность
.
9.
Плотность вещества
- масса единицы объема вещества:
.
Размерность
.
8.2. Уравнение состояния идеального газа
Одним из первых достижений молекулярной физики является создание теории идеальных газов. Если взаимодействием между молекулами можно пренебречь, то газ называется идеальным Близок к идеальному реальный газ при низких температурах, невысоких давлениях и малой концентрации частиц.
Состояние
идеального газа можно описать с помощью
трех параметров: давления, абсолютной
температуры и объема. Эти характеристики
являются результатом усреднения по
большому числу частиц системы. Давление
измеряется в Паскалях:
,
абсолютная температура измеряется в
Кельвинах:
,
размерность объема:
Уравнение состояния идеального газа
(8.1)
Для
1 моля вещества,
где
- универсальная газовая постоянная.
Рис. 8.1.
Запишем
газовые законы для изопроцессов,
происходящих при условии, что один из
параметров: температура
,
давление P
или объём
остаются постоянными.
Закон Бойля-Мариотта (изотермический процесс: T = const, m = const): При неизменных температуре и массе произведение численных значений давления и объёма газа постоянно:
(8.2)
или для двух состояний газа:
График
изотермы на диаграмме
приведён
на рис. 8.1.
Закон
Гей – Люссака
(изобарный
процесс:
,
):
При постоянном
давлении объём данной массы газа прямо
пропорционален его абсолютной температуре:
(8.3)
или для двух различных состояний:
.
График
изобары на диаграмме
приведён на рис. 8.2.
Рис. 8.2. Рис. 8.3.
Закон Шарля (изохорный процесс: V = const, m = const): При постоянном объёме давление данной массы газа прямо пропорционально его абсолютной температуре:
(8.4)
или для двух состояний:
.
График изохоры на диаграмме РТ приведён на рис. 8.3.
Уравнение состояния идеального газа для произвольного количества вещества называется уравнением Менделеева - Клапейрона:
(8.5)
Найдём
число молекул, содержащихся в единице
объёма идеального газа. Запишем уравнение
Менделеева – Клапейрона в виде:
,
откуда находим:
(8.6)
где
- постоянная Больцмана:
.
Менделеев Дмитрий Иванович (1834 - 1907), русский учёный, родился в Тобольске. Окончил Главный педагогический институт в Петербурге. Открыл в 1862 г. один из фундаментальных законов природы - периодический закон химических элементов, нашёл общее уравнение состояния идеального газа (уравнение Менделеева-Клапейрона). Сконструировал барометр. В 1888 г. выдвинул идею подземной газификации угля.
Клапейрон Бенуа Поль Эмиль (1799 - 1864), французский физик и инженер, родился в Париже. Окончил Политехническую школу. Физические исследования посвящены теплоте, пластичности и равновесию твёрдых тел. Ввёл в термодинамику метод диаграмм, в частности, предложил систему координат . В 1834 г. вывел уравнение состояния идеального газа и уравнение, устанавливающее связь между температурой плавления и кипения вещества и давлением - уравнение Клапейрона - Клаузиуса.
Для смеси идеальных газов выполняется закон Дальтона:
(8.7)
где
- парциальное давление компонентов
смеси;
- число компонентов смеси;
,
- установившиеся объем и температура
смеси газов.
Парциальным давлением i-го компонента смеси называется давление газа при условии, что установившийся объем заполнен только этим компонентом и температура равна температуре смеси.
Количество вещества смеси газов:
,
или
(8.8)
где
- количество вещества, число молекул,
масса и молярная масса i-го
компонента смеси, соответственно.
Молярная масса смеси газов:
(8.9)