7.3. Математический маятник

М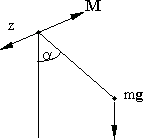 аятником называется твердое тело, совершающее колебания под действием силы тяжести вокруг неподвижной точки или оси, не проходящей через его центр тяжести.

М

79

атематический маятник - это идеализированная система из невесомой и нерастяжимой нити и материальной точки массой m на конце нити (рис. 7.3).

П

Рис. 7.3.

ри отклонении маятника возникает вращательный момент, проекция его на ось вращения z

(7.13)

Знак минус показывает, что момент стремится вернуть маятник в положение равновесия. Запишем основное уравнение вращательного движения, т.к. колебательное движение здесь является частью вращательного:

где L - момент импульса тела, или в скалярном виде

здесь - момент инерции материальной точки с массой m относительно оси вращения z;

- угловое ускорение материальной точки.

Получим уравнение

Разделим левую и правую части уравнения на , получим

.

Рассмотрим малые колебания маятника, тогда .

Уравнение гармонических колебаний математического маятника имеет вид

(7.14)

Запишем его в виде

(7.15)

где - частота колебаний.

Период колебаний

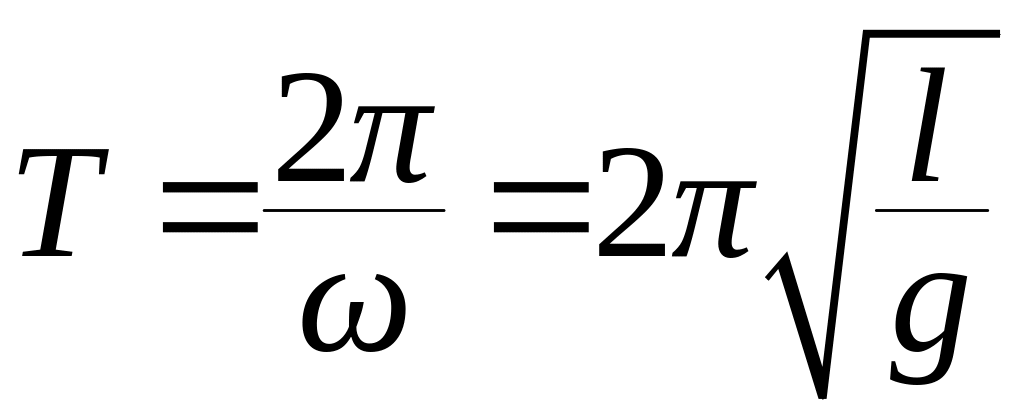(7.16)

Находим решение

(7.17)

При малых колебаниях угловое отклонение математического маятника изменяется со временем по гармоническому закону.

7.4. Физический маятник

Маятник называется физическим, если колеблющееся тело нельзя представить в виде материальной точки, т.е. пренебречь его

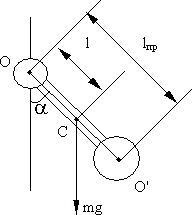
Рис. 7.4.

размерами (рис. 7.4).

Запишем уравнение динамики вращательного движения твердого тела:

,

где M - момент силы тяжести;

L - момент импульса маятника.

Проекция момента силы на ось вращения z имеет вид

,

где - расстояние между точкой подвеса 0 и центром масс С маятника.

Получим уравнение движения

где J – момент инерции маятника относительно оси колебаний, проходящей через точку подвеса 0.

В случае малых колебаний

(7.18)

где 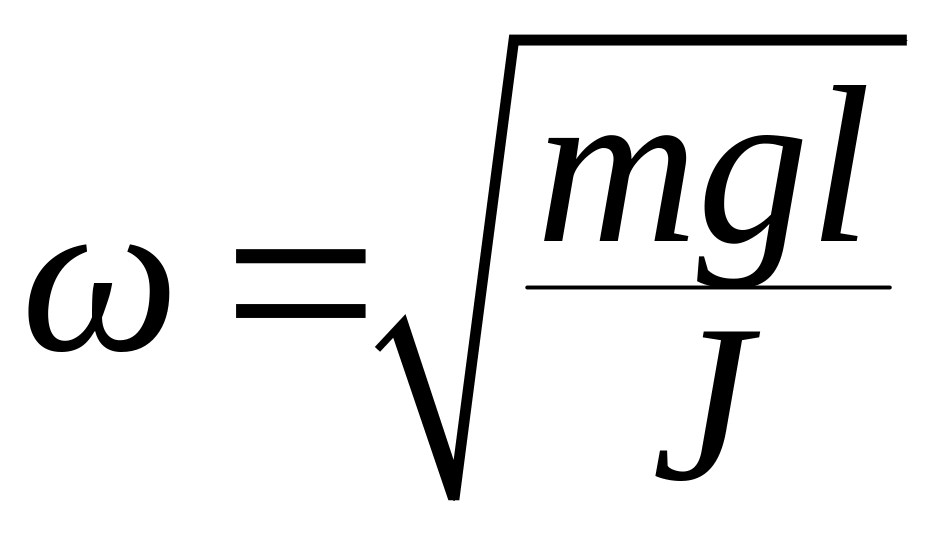- частота колебаний физического маятника.

Физический маятник при малых колебаниях совершает гармоническое движение с периодом

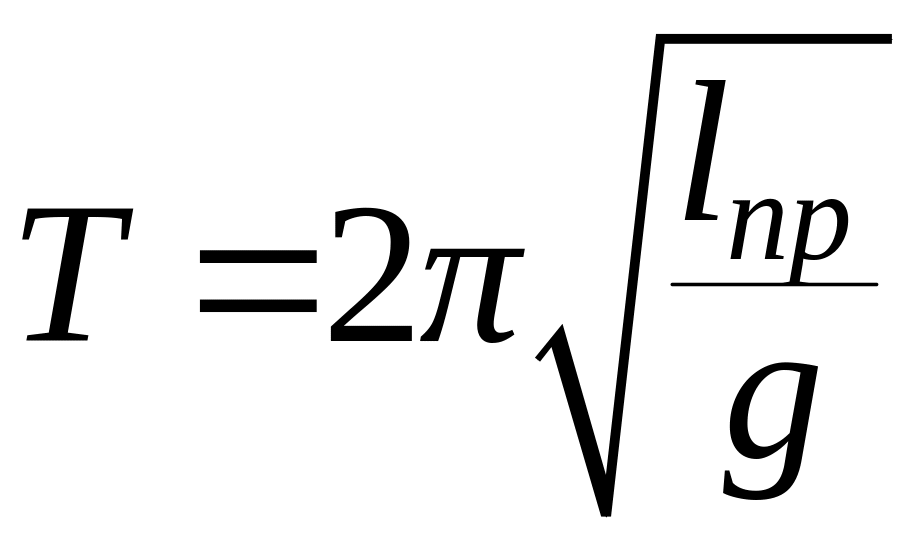(7.19)

Сравнивая полученное выражение с периодом математического маятника, получим

(7.20)

где - приведенная длина физического маятника.

Приведенная длина физического маятника - это длина математического маятника, имеющего период колебаний, равный периоду колебаний данного физического маятника.

Точка O, лежащая на прямой, соединяющей точку подвеса с центром масс С, называется центром качания маятника. Расстояние между точками O и O равно приведенной длине физического маятника. Эти точки обладают свойством взаимности. Если точка O станет точкой подвеса, то центром качания станет точка O.

Это свойство используется при определении ускорения свободного падения методом оборотного маятника:

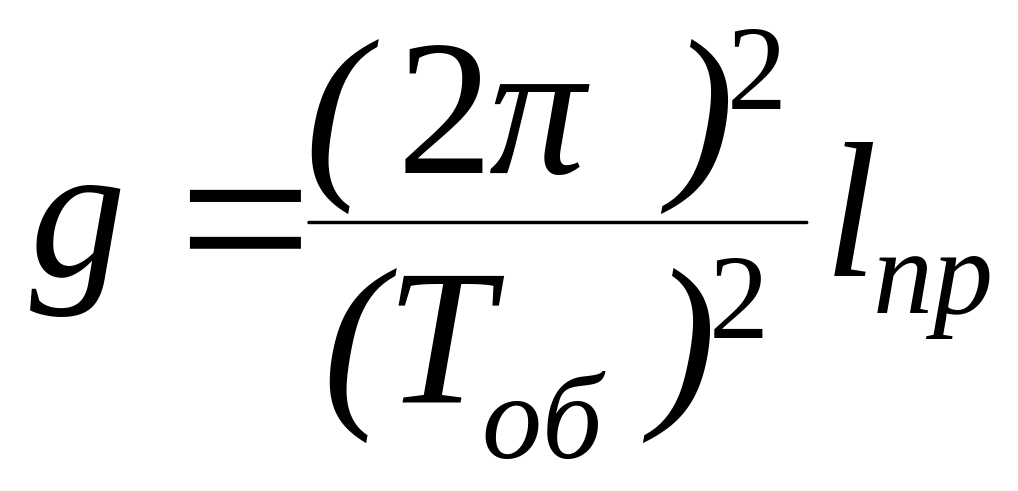(7.21)

Из выражения (7.21) следует

.

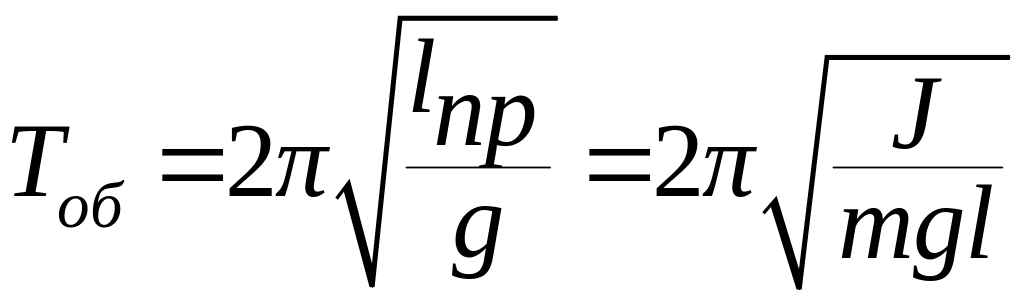Период колебания оборотного маятника можно найти графически, как точку пересечения зависимостей и от положения подвижного груза на стержне маятника.

7.5. Сложение колебаний Сложение одинаково направленных колебаний

83

Пусть имеются два гармонических колебания одинакового направления, совершающиеся вдоль оси х с одинаковой частотой . Амплитуды и начальные фазы колебаний могут быть различными. В качестве механической модели для изучения сложения колебаний рассмотрим груз массой m, укрепленный на двух последовательно соединенных пружинах с одинаковой жесткостью k (рис. 7.5).

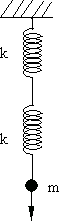
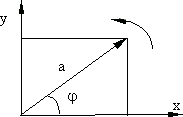
Рис. 7.5. Рис. 7.6.

Гармоническое колебание можно представить с помощью вектора, образующего с осью х угол, равный начальной фазе колебаний и длиной, равной амплитуде колебаний a (рис. 7.6). Проекция вектора на ось x совершает гармоническое колебание с амплитудой a и частотой :

(7.22)

Если имеются два гармонических колебания, то их можно также изобразить на векторной диаграмме (рис. 7.7).

Здесь .

, ,

;

. (7.23)

Найдем тангенс фазы и квадрат амплитуды результирующего колебания

,

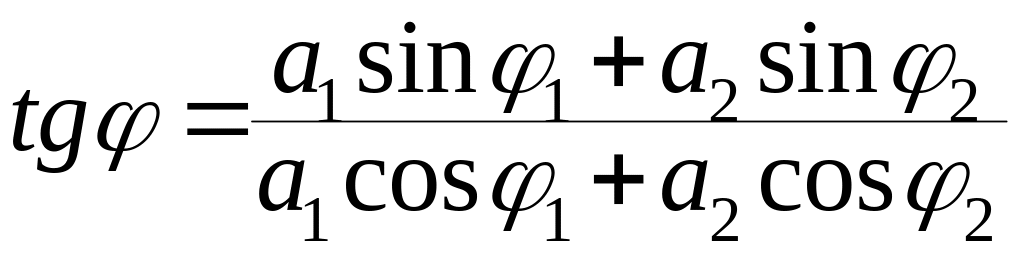(7.24)

Рассмотрим возможные результаты сложения одинаково направленных колебаний в зависимости от разности фаз между этими колебаниями.

1. Пусть , тогда , амплитуда результирующего колебания равна сумме амплитуд:

.

2. Пусть , тогда , амплитуда результирующего колебания равна модулю разности амплитуд:

В зависимости от разности фаз амплитуда результирующего колебания может увеличиваться или уменьшаться. Наибольшее усиление колебаний происходит в случае одинаковых фаз, а наибольшее ослабление в случае противофаз.

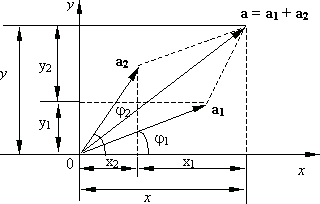
Рис. 7.7.