§24. Начальные и центральные теоретические моменты

Рассмотрим дискретную случайную величину ξ, заданную законом распределения:

ξ	1	2	5	100
P	0,6	0,2	0,19	0,01

Найдем математическое ожидание ξ:

М(ξ)=1·0,6+2·0,2+5·0,19+100·0,01=2,95.

Напишем закон распределения ξ ²:

ξ2	1	4	25	10000
P	0,6	0,2	0,19	0,01

Найдем математическое ожидание ξ ²:

М(ξ ²)=1·0,6+4·0,2+25·0,19+10000·0,01=106,15.

Видим, что М(ξ²) значительно больше М(ξ). Это объясняется тем, что после возведения в квадрат возможное значение величины ξ², соответствующее значению x₄=100 величины ξ, стало равным 10000, то есть значительно увеличилось; вероятность же этого значения мала (0,01).

Таким образом, переход от М(ξ) к М(ξ²) позволил лучше учесть влияние на математическое ожидание того возможного значения, которое велико и имеет малую вероятность. Разумеется, если бы величина ξ имела несколько больших и маловероятных значений, то переход к величине ξ², а тем более к величинам ξ³, ξ⁴ и т. д., позволил бы еще больше «усилить роль» этих больших, но маловероятных возможных значений. Вот почему оказывается целесообразным рассматривать математическое ожидание целой положительной степени случайной величины (не только дискретной, но и непрерывной).

Определение. Начальным моментом порядка k случайной величины ξ называют математическое ожидание величины ξ^k:

ν_k=M(ξ^k).

В частности,

ν₁=M(ξ), ν₂=M(ξ²).

Пользуясь этими моментами, формулу для вычисления дисперсии

D(ξ)=M(ξ²)-[M(ξ)]²

можно записать так:

D(ξ)=ν₂-ν .

Кроме моментов случайной величины ξ целесообразно рассматривать моменты отклонения ξ-М(ξ).

Определение. Центральным моментом порядка k случайной величины ξ называют математическое ожидание величины (ξ-М(ξ))^k:

µ_k=M[(ξ-М(ξ))^k].

В частности,

µ₁=M[(ξ-М(ξ))]=0,

µ₂=M[(ξ-М(ξ))²]=D(ξ).

Легко выводятся соотношения, связывающие начальные и центральные моменты. Например,

µ₂=ν₂-ν .

Нетрудно, исходя из определения центрального момента и пользуясь свойствами математического ожидания, получить формулы:

µ₃=ν₃–3ν₂ν₁+2ν ,

µ₄=ν₄–4ν₃ν₁+6ν₂ν -3ν .

Моменты более высоких порядков применяются редко.

§25. Числовые характеристики непрерывных случайных величин

Распространим определения числовых характеристик дискретных величин на величины непрерывные. Начнем с математического ожидания.

Пусть непрерывная случайная величина ξ задана плотностью распределения f(x). Допустим, что все возможные значения ξ принадлежат отрезку [а,b]. Разобьем этот отрезок на п частичных отрезков длиной Δx₁,Δx₂,...,Δх_п и выберем в каждом из них произвольную точку х_i (i=1,2,...,п). Нам надо определить математическое ожидание непрерывной величины по аналогии с дискретной; составим сумму произведений возможных значений x_i на вероятности попадания их в интервал Δх_i (произведение f(x) ∆x приближенно равно вероятности попадания ξ в интервал ∆x ):

f(x_i) ∆x_i.

Перейдя к пределу при стремлении к нулю длины наибольшего из частичных отрезков, получим определенный интеграл .

Определение. Математическим ожиданием непрерывной случайной величины ξ, возможные значения которой принадлежат отрезку [а,b], называют определенный интеграл

M(ξ)= .

Если возможные значения принадлежат всей оси OX, то

M(ξ)= .

Предполагается, что несобственный интеграл сходится абсолютно, то есть существует интеграл f(x)dx. Если бы это требование не выполнялось, то значение интеграла зависело бы от скорости стремления (в отдельности) нижнего предела к минус бесконечности (-∞), а верхнего - к плюс бесконечности (+∞).

По аналогии с дисперсией дискретной величины определяется и дисперсия непрерывной величины.

Определение. Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.

Если возможные значения ξ принадлежат отрезку [а,b], то

D(ξ)= f (x)dx;

если возможные значения принадлежат всей оси х, то

D(ξ)= f(x)dx.

Определение. Среднее квадратическое отклонение непрерывной случайной величины определяется, как и для величины дискретной, равенством

σ(ξ)= .

Замечание. Можно доказать, что свойства математического ожидания и дисперсии дискретных величин сохраняются и для непрерывных величин.

Легко получить для вычисления дисперсии более удобные формулы:

D(ξ)= f(x)dx–[M(ξ)]²,

D(ξ)= f(x)dx–[M(ξ)]²,

Пример. Найти математическое ожидание и дисперсию случайной величины ξ, заданной функцией распределения

F(х)=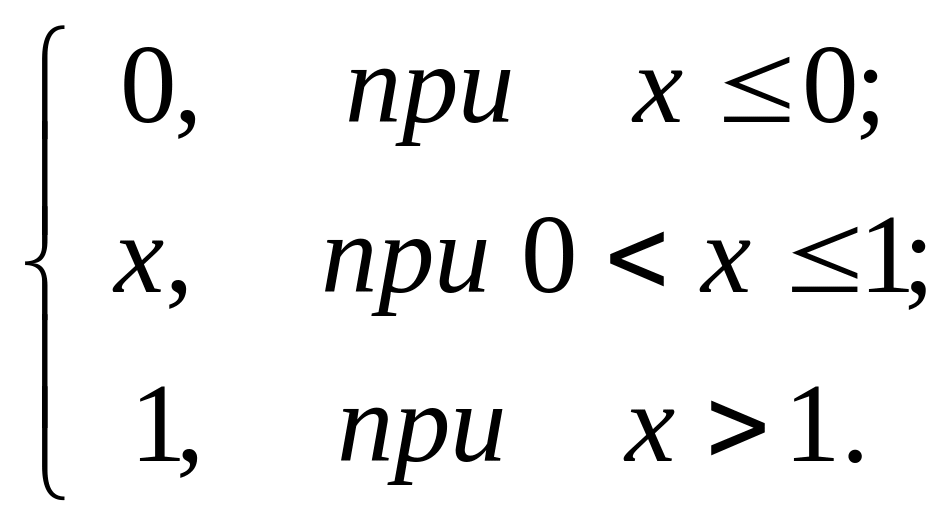

Решение. Найдем плотность распределения:

f(х)=F’(х)=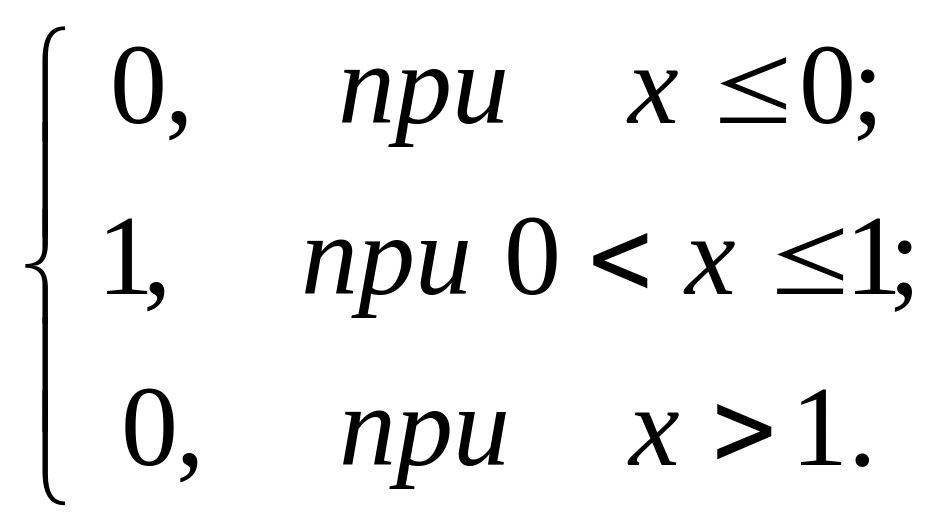

Найдем математическое ожидание

M(ξ)= =x²/2| =1/2.

Найдем дисперсию:

D(ξ)= ·1·dx–[1/2]²=x³/3| -1/4=1/12.

Числовые характеристики равномерного распределения.

Найти математическое ожидание и дисперсию непрерывной случайной величины ξ, распределенной равномерно в интервале (а,b).

Решение. Найдем математическое ожидание ξ, учитывая, что плотность равномерного распределения f(х)=1/(b-а).

M(ξ)= = .

Выполнив элементарные выкладки, получим

M(ξ)=(a+b)/2.

Найдем дисперсию ξ:

D(ξ)= f(x)dx–[M(ξ)]²= - .

Выполнив элементарные выкладки, получим

D(ξ)=(b-a)²/12.

Замечание. Математическое ожидание и дисперсия случайной величины R, распределенной равномерно в интервале (0;1), т.е. если а=0, b=1, как следует из предыдущего примера, соответственно равны М(R)=1/2, D(R)=1/12. Этот же результат мы получили в примере по заданной функции распределения случайной величины R.

Числовые характеристики показательного распределения.

Пусть непрерывная случайная величина ξ распределена по показательному закону

f(x)=

Найдем математическое ожидание:

М(ξ)= f(x)dx=λ e^-λxdx.

Интегрируя по частям, получим

М(ξ)=1/λ.

Таким образом, математическое ожидание показательного распределения равно обратной величине параметра λ. Найдем дисперсию:

D(ξ)= f(x)dx–[M(ξ)]²=λ e^-λx dx-1/λ².

Интегрируя по частям, получим

λ e^-λx dx=2/λ².

Следовательно,

D(ξ)=1/λ².

Найдем среднее квадратическое отклонение, для чего извлечем квадратный корень из дисперсии:

σ(ξ)=1/λ.

Окончательно заключаем, что

М(ξ)=σ(ξ)=1/λ,

то есть математическое ожидание и среднее квадратическое отклонение показательного распределения равны между собой.

Пример. Непрерывная случайная величина ξ распределена по показательному закону f(x)=5e^-5x при х≥0; f(x)=0 при х<0.

Найти математическое ожидание, среднее квадратическое отклонение и дисперсию ξ.

Решение. По условию, λ=5. Следовательно,

М(ξ)=σ(ξ)=1/λ=1/5=0,2;

D(ξ)=1/λ²=1/5²=0,04.

Числовые характеристики нормального распределения.

Пусть случайная величина имеет нормальное распределение

f(x)= e .

Мы видим, что нормальное распределение определяется двумя параметрами: a и σ. Достаточно знать эти параметры, чтобы задать нормальное распределение. Покажем, что вероятностный смысл этих параметров таков: а есть математическое ожидание, σ - среднее квадратическое отклонение нормального распределения.

а) По определению математического ожидания непрерывной случайной величины,

M(ξ)= .

Введем новую переменную z=(x-а)/σ. Отсюда x=σz+a, dx=σdz. Приняв во внимание, что новые пределы интегрирования равны старым, получим

M(ξ)= σz + a) e dz=

= ze dz+ dz.

Первое из слагаемых равно нулю (под знаком интеграла нечетная функция; пределы интегрирования симметричны относительно начала координат). Второе из слагаемых равно а (интеграл Пуассона dz= ).

Итак, М(ξ)=а, то есть математическое ожидание нормального распределения равно параметру а.

б) По определению дисперсии непрерывной случайной величины, учитывая, что М(ξ)=а, имеем

D(ξ)= x-a)² e dx

Введем новую переменную z=(х—а)/σ. Отсюда х–a=σz, dx=σdz. Приняв во внимание, что новые пределы интегрирования равны старым, получим

D(ξ)= ·ze dz

Интегрируя по частям, положив u=z, dυ=ze dz, найдем

D(ξ)=σ².

Следовательно,

σ(ξ)= = =a.

Итак, среднее квадратическое отклонение нормального распределения равно параметру σ.

Определение. Асимметрией теоретического распределения называют отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:

A_s=µ₃/σ³.

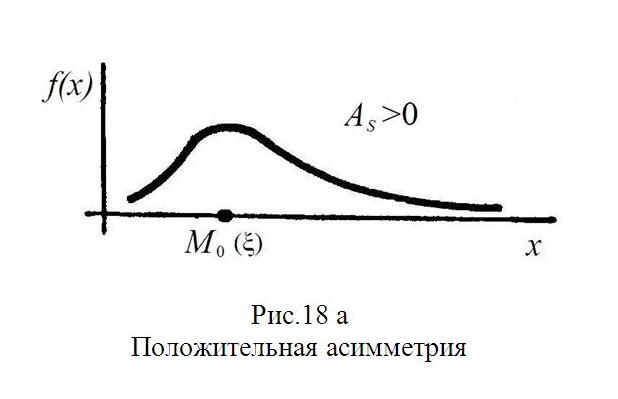
Асимметрия положительна, если «длинная часть» кривой распределения расположена справа от математического ожидания; асимметрия отрицательна, если «длинная часть» кривой расположена слева от математического ожидания. Практически определяют знак асимметрии по расположению кривой распределения относительно моды (точки максимума дифференциальной функции): если «длинная часть» кривой расположена правее моды, то асимметрия положительна (рис.18а), если слева – отрицательна (рис.18б). Для оценки «крутости», то есть большего или меньшего подъема кривой теоретического распределения по сравнению с нормальной кривой, пользуются характеристикой - эксцессом.

Определение. Эксцессом теоретического распределения называют характеристику, которая определяется равенством

E_k=(µ₄/σ⁴)–3.

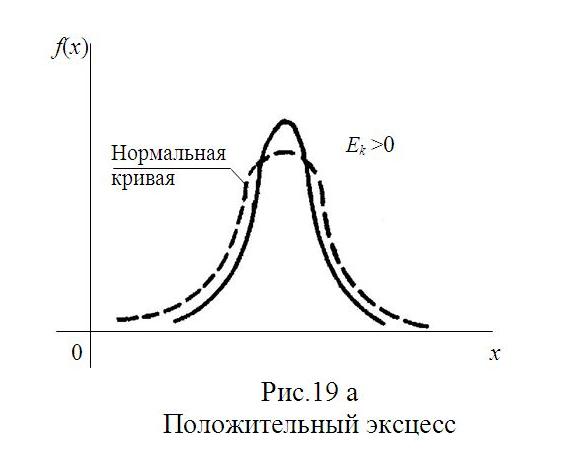
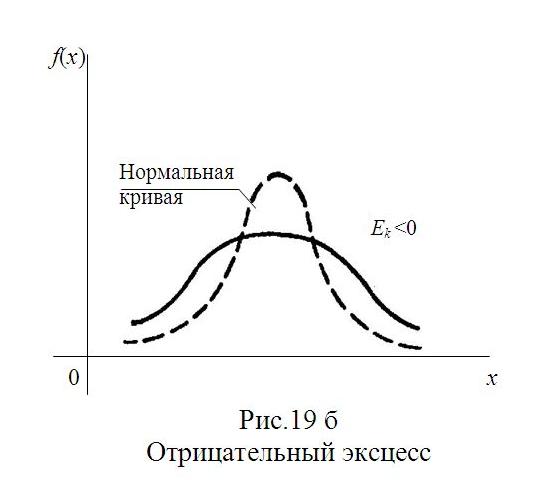
Для нормального распределения µ₄/σ⁴=3; следовательно, эксцесс равен нулю. Поэтому если эксцесс некоторого распределения отличен от нуля, то кривая этого распределения отличается от нормальной кривой: если эксцесс положительный, то кривая имеет более высокую и «острую» вершину, чем нормальная кривая; если эксцесс отрицательный, то сравниваемая кривая имеет более низкую и «плоскую» вершину, чем нормальная кривая. При этом предполагается, что нормальное и теоретическое распределения имеют одинаковые математические ожидания и дисперсии.