3.2. Методика составления дифференциальных уравнений

_{1. Установление физического закона протекания процессов.}

_{Математическое выражение закона образует дифференциальное уравнение.}

_{2. Выявление и анализ факторов для определения зависимостей переменных, входящих в исходное уравнение. Нахождение математических зависимостей, как правило, нелинейных функций.}

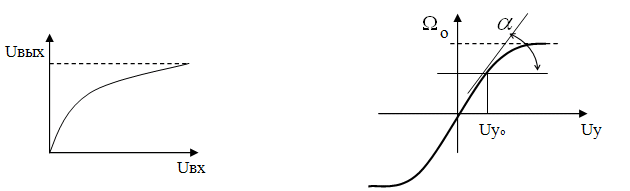
_{Рис. 24. Статическая характеристика Рис. 25. Характеристика холостого хода}

_{усилителя постоянного тока двигателя постоянного тока}

_{3. Линеаризация (если она допустима), упрощающая исследование процессов.}

_{Признаки допустимости линеаризации следующиеи:}

_{а) отсутствие разрывных, неоднородных и резко меняющихся функций;}

_{б) правомерность уравнения для всего интервала регулирования}

₍₈₎

_{Дифференциальные уравнения линеаризуют при помощи формулы Тейлора разложением нелинейных функций нескольких переменных по степеням их малых приращений в окрестности значений, соответствующих установившемуся режиму.}

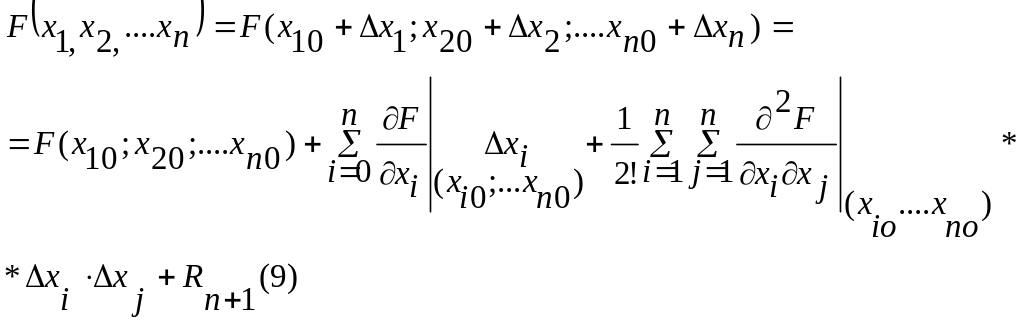_{где xi=xi0+xi; xi0=соnst; Rn+1 – остаточный член.}

_{Обычно ограничиваются членами первого порядка малости, пренебрегая Rn+1 , тогда}

₍₁₀₎

_{и получаем дифференциальное уравнение в приращениях}

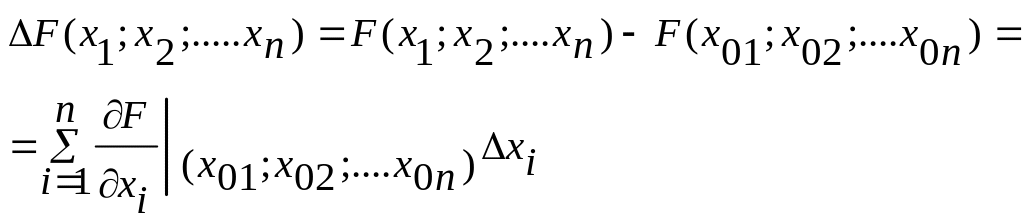₍₁₁₎

_{4. Преобразование дифференциальных уравнений к безразмерному виду. Переменные выражаются в относительных единицах, а коэффициенты безразмерны или имеют размерность времени в степени, соответствующей порядку производной величины к которой он относится.}

_{Порядок преобразований следующий:}

_{а) все члены уравнения делятся на некоторые постоянные значения переменной имеющей размерность членов уравнения;}

_{б) переход к относительным единицам. Выбирают некоторое постоянное значение каждой переменной и определяют соотношения приращений и выбранных постоянных значений;}

_{в) вводят обозначения относительных единиц и коэффициентов.}

_{Рассмотрим линейные колебания подвижной массы при кинематическом возмущении.}

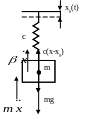
_{Рис. 26. Подвижная масса при кинетическом возмущении}

_{Условия кинетического воздействия:}

₍₁₂₎

(13)

(14)

_{где с – жесткость упругого элемента;}

_{β – коэффициент сопротивления.}

_{Введем новую переменную z=y/xст .}

Выполнив преобразование получим , (15)

где ;

– постоянная времени (период). (16)

_{Имея линейные уравнения отдельных звеньев САР, путем последовательного исключения промежуточных переменных можно получить дифференциальное уравнение замкнутой системы в виде:}

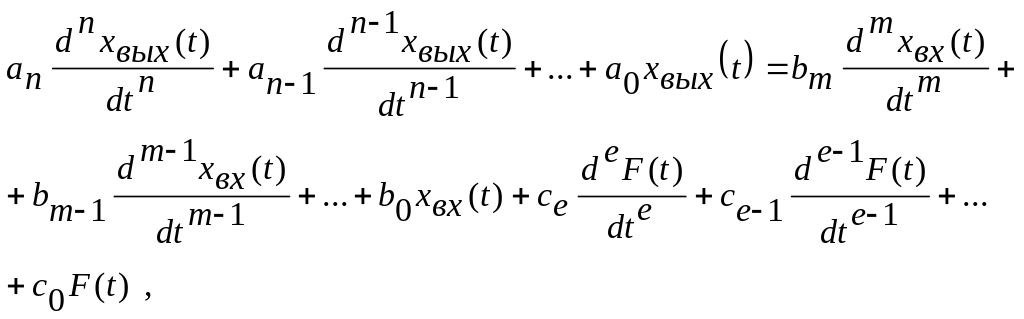₍₁₇₎

где х_вх(t) – входная величина; х_вых(t) – выходная величина; F(t) – возмущающее воздействие;

_{ai;bj;ck – постоянные коэффициенты.}

Левая часть уравнения равная нулю характеризует свойства системы, а правая часть – воздействие, поданное на вход САР, причем nm.

В теории автоматического регулирования для анализа уравнений движения широко используется преобразование Лапласа.

Если f(t)=0 при t<0 то преобразование Лапласа:

(18)

и дифференциальное уравнение можно записать (при нулевых начальных условиях) в виде:

(19)

Если ввести обозначения

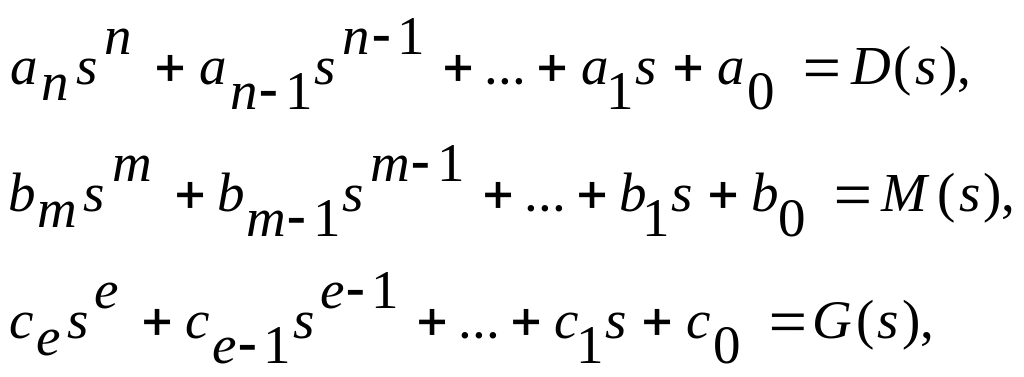(20)

то дифференциальное уравнение примет вид

(21)

Если f(t)=0, то

(22)

_{называется передаточной функцией системы по отношению к управляющему воздействию.}

_{Передаточная функция САР обладает следующими свойствами:}

1. передаточная функция – дробно-радиальная функция вида

(23)

и для реальной системы m > n:

2) коэффициенты a_n …a_o ,b_m …b_o вещественны;

3) невещественные корни многочленов числителя и знаменателя могут быть только комплексно-сопряженными;

4. корни уравнений M(s) = 0 называются нулями, D(s) = 0 называются полюсами.

При замене оператора s на частотный оператор получаем частотную передаточную функцию

₍₂₄₎