7.2. Алгебраический критерий устойчивости Гурвица

Устойчивость замкнутой динамической системы, имеющей характеристическое уравнение,

(80)

определяется выполнением следующих условий:

1. коэффициенты характеристических уравнений положительны (необходимое условие);

2. определители – диагональные миноры, образованные последовательным выделением по строкам и столбцам из главного определителя.

₁  0 ₂  0 ₃  0 _n-1  0

начиная с ₁=a_n-1  0 (достаточное условие).

Определитель _n составляется следующим образом: главная диагональ состоит из коэффициентов характеристического уравнения. Начиная со второго коэффициента в порядке убывания индексов, заполняются строки: слева – в порядке убывания индексов, справа – в порядке вырастания.

7.3. Частотные критерии устойчивости Критерий Михайлова

Х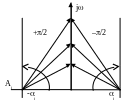 арактеристическое уравнение замкнутой САР:

D₃(s) =D(s)+M(s)=0

Разложив на множители, получим:

D₃(s)=(s-s₁)(s-s₂)…(s-s_n).

После перехода к частотному оператору

D₃(j)=(j-s₁) (j-s₂)…(j-s_n)

Рис.61. Комплексная плоскость

Каждый из корней s_i может быть представлен точкой A_i на комплексной плоскости. Каждому значению оператора jω соответствует точка мнимой оси В_i. Следовательно, положения точек А_i и В_i на комплексной плоскости изображаются векторами s_i и jω, а каждый из сомножителей (jω–s_i ) разностным вектором V_i.

При изменении ω от 0 до  вектор V_i будет вращаться вокруг полюса s_i (точка А_i). Направления вращения и угол поворота векторов V_i зависит от значения корней s_i.

Случай 1. Корни вещественные: s_i=_i.

Если s_i=-α_i, то будем считать поворот положительным (+π/2), при р_i>0 – (-π/2).

С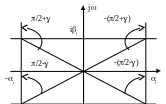 лучай 2. Корни комплексно-сопряженные:

s_i=_ij_i

Если α_i<0, то .

Если α_i>0, то

Рис. 62. Комплексная плоскость

Каждый вектор можно представить следующим образом:

, = arg .

Следовательно , D₃(p)= . (81)

Пусть из всех n корней m – положительны, n - m – отрицательны, k – вещественные, m - k – комплексные, s – вещественные, n - m - s – комплексные, тогда суммарный угол поворота векторов

= S,

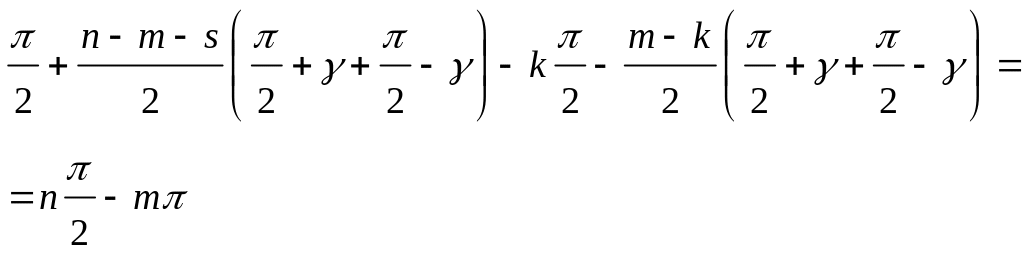(82)

Для устойчивой замкнутой САР, когда m=0 , условие устойчивости

(83)

Система устойчива, если суммарный угол поворота вектора D₃(j) равен n/2, то есть характеристическая кривая (годограф Михайлова) должна пересечь поочерёдно n раз минимум и вещ. оси.

На рис.63 и 64 показаны годографы АФЧХ некоторых САР, где D₃(j)=Y(+φζ()).

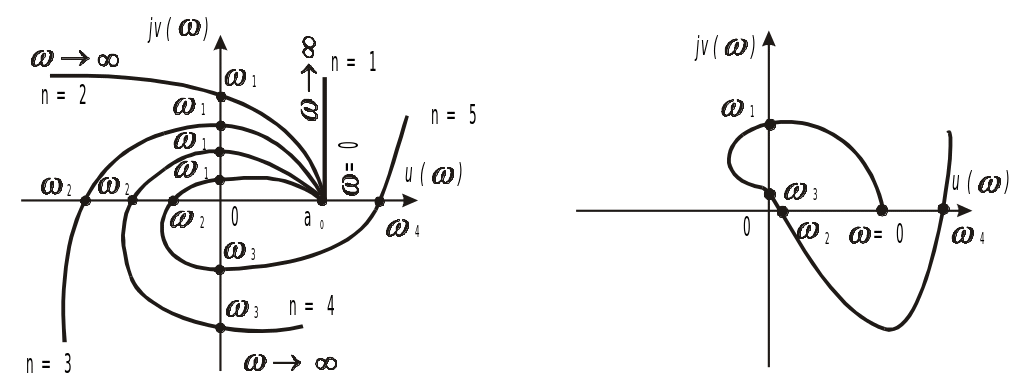
Рис. 63. Годографы устойчивых Рис. 64. Годограф неустойчивой систем (n=1..5) системы (n=5)

Если годограф проходит через начало координат, то САР – критическая.

Устойчивость САР может быть определена по вещественным частотным характеристикам.

Рис. 65. Вещественная и мнимая части Рис. 66. Вещественная и мнимая части й

D₃(j) устойчивой АС (n=5) D₃(j) неустойчивой АС (n=5)

АС будет устойчивой, если корни вещественной и мнимой частей кривой D₃(j) перемежаются и их число равно порядку уравнения.

Годографы дают возможность:

1) судить о “запасе” устойчивости по сближению корней;

2) обнаружить наиболее опасные частоты.

При смещении годографа вправо, т.е. при увеличении коэффициента усиления САР (увеличения а₀) запас устойчивости снижается.

Недостаток метода заключается в необходимости анализа характеристического уравнения САР в замкнутом состоянии.