12.2. Фильтрация помех

Задача фильтрации заключается в том, что если на вход САР подается стационарный случайный сигнал (t) = m(t) + n(t), где m(t) – полезный сигнал, n(t) – помеха, то САР должна воспроизводить полезный сигнал m(t) с минимальной СКО

В этом случае h(t) = m(t) и S_h() = S_m()=S_m()+S_mn(), так как в большинстве случаев сигналы m(t) и n(t) независимы и S_() = S_m()+S_n().

Тогда передаточная функция фильтра определяется соотношением

(183)

Определим СКО при условии удовлетворения оптимума

(184)

Используя обратное преобразования Фурье и поменяв порядок интегрирования во втором слагаемом, получим

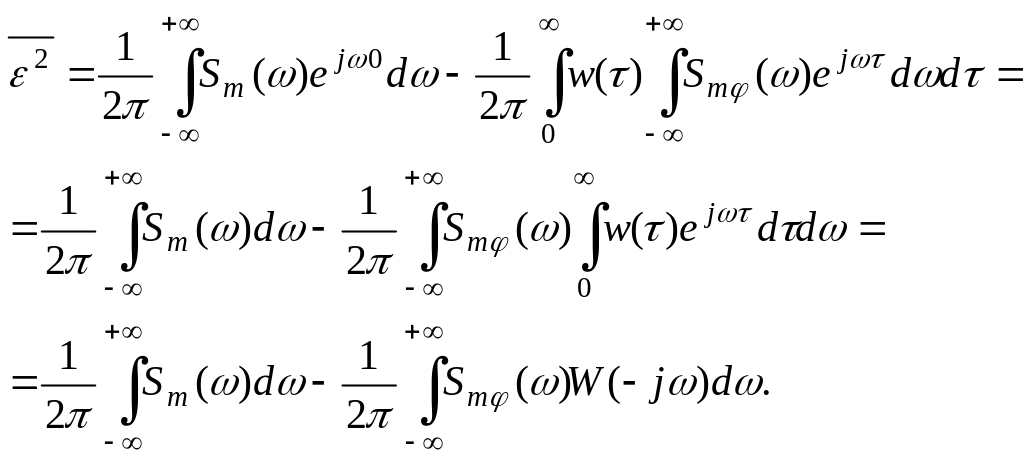(185)

Заменим и, принимая во внимание, что получим

. (186)

Контрольные вопросы:

1. Из чего состоят ошибки САР?

2. Что такое среднеквадратическая ошибка системы?

3. Что определяет критерий среднеквадратической ошибки?

4. Какие могут быть варианты решения задачи синтеза САР?

5. В чем заключается сущность метода, предложенная Н. Винером?

6. Что возможно сделать на основании минимума критерия среднеквадратической ошибки для оптимизации системы?

7. В чем заключается метод фильтрации помех?

Лекция 13. Линейные нестационарные системы. Методы анализа динамики и синтеза структурных схем. Основные принципы построения адаптивных систем

13.3. Линейные нестационарные и адаптивные сар

Расширение областей применения САР и возрастающие требования к точности, особенно в переходных режимах, требуют учета изменения параметров в процессе регулирования.

Наиболее характерны изменения параметров объекта регулирования, например: изменение аэродинамических свойств летательных аппаратов при посадке или преодолении звукового барьера. Поведение таких объектов описывается дифференциальными уравнениями с переменными коэффициентами. Такие объекты и САР, включающие их, называются нестационарными.

Анализ нестационарных систем с математической точки зрения представляет сложную задачу и получение замкнутых решений дифференциальных уравнений с переменными коэффициентами в большинстве случаев не представляется возможным.

В настоящее время существуют два подхода к решению проблем управления нестационарными объектами:

а) синтез САР с «жестким» основным контуром.

В этом случае подбирается необходимый набор фильтров и коррелирующих элементов.

б) синтез САР с «гибким» основным контуром. Вводятся дополнительные регуляторы, обеспечивающие изменение параметров системы, в результате чего САР «приспосабливается» к объекту регулирования. Такие САР называются «адаптивными».

Для решения дифференциального уравнения с переменными коэффициентами вида

применяются следующие методы:

1. «замораживания коэффициентов». Для выбранного интервала времени коэффициенты характеристического уравнения считаются постоянными величинами.

2. расщепление дифференциального уравнения динамики САР:

• на ряд дифференциальных уравнений, характеризующих отдельные парциальные движения с последующей суперпозицией;

• на отдельные фазы, следующие друг за другом;

3. спектральные методы.

• метод нестационарных спектральных характеристик функций времени;

• разложение решений в ряд Фурье;

4. численные методы базирующихся на ЭВМ;

5. цифровое имитационное моделирование.

Рассмотрим спектральный (полуаналитический) метод исследования переходных процессов. Метод предполагает построение решения в виде усеченного ряда по некоторой системе ортогональных функций, удовлетворяющих заданным граничным условиям. Под спектром понимается совокупность коэффициентов Фурье-разложения. Задача заключается в определении этого спектра.

Пусть требуется определить решение уравнения

(187)

на интервале [0; R], удовлетворяющее на границах интервала следующим условиям:

Применяя подстановку y(x) = Y(x) + h(x), где h(x) – произвольная функция, которая обращает граничные условия y^(k) = 0; (k = 0, 1, …).

Тогда уравнение приобретает вид

, (188)

где

. (189)

Удобно принять

. (190)

Коэффициент h_m определяется из условия обнуления y на границах.

Ищем Y(x) в виде разложения по синусам или косинусам на заданном интервале [0; R]

(191)

или

(192)

Перемножим уравнение на и проинтегрируем на интервале [0; R]:

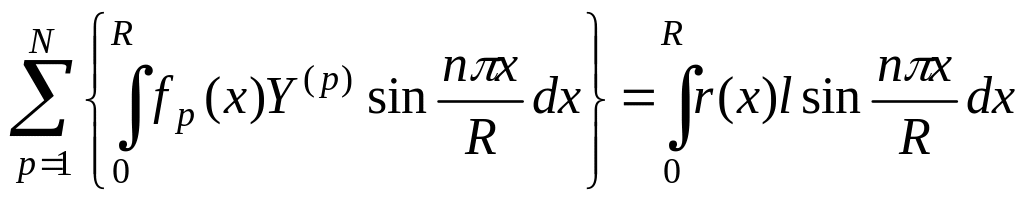(193)

В этом уравнении f_K(x) раскладывается в ряды Фурье:

при четных k (k=2p) – по косинусам:

; (p = 0, 1, 2, …), (194)

при нечетных k (k=2p+1) – по синусам

; (p = 0, 1, 2, …), (195)

где

(196)

(197)

Этими действиями исходное уравнение сводится к системе алгебраических уравнений относительно коэффициентов в_q.

Общие выражения алгебраических уравнений позволяют сразу записать алгебраические уравнения по исходному дифференциальному уравнению [187].

Решение алгебраических уравнений производится известными методами.