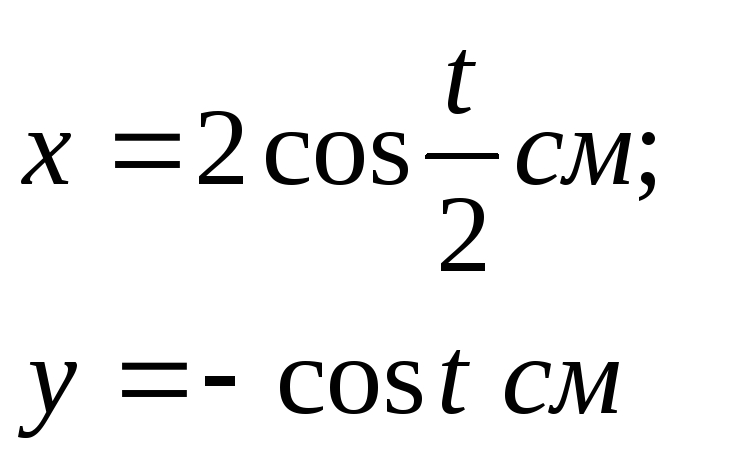6. Волновое число, фазовая скорость.

7. Для характеристики волн используется волновое число

Предположив, что при волновом процессе фазы постоянны, получим, что скорость V распространения волны есть не что иное, как скорость перемещения фазы волны, и ее называют фазовой скоростью:

7. Волновое уравнение.

Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением – дифференциальным уравнением в частных производных

(3.7)

или

где V – фазовая скорость.

8. Уравнение стоячей волны.

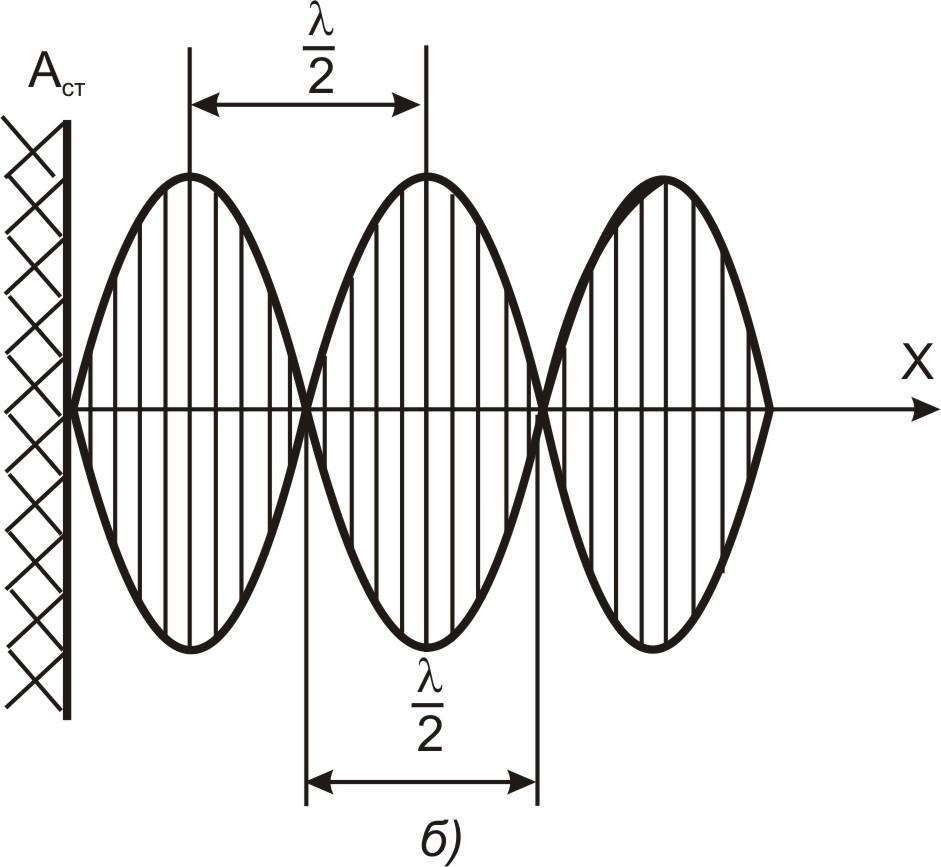
Рис. 3.6

Сложив эти уравнения и учитывая, что k = 2π / λ, получим уравнение стоячей волны:

ξ = ξ₁+ ξ₂ = 2A cos kx cos ωt = 2A cos (2πx/λ)cos ωt. (3.8)

Из уравнения стоячей волны вытекает, что в каждой точке этой волны происходят колебания той же частоты ω с амплитудой

А_ст = │2Аcos (2πx/λ)│, зависящей от координаты х рассматриваемой точки.

В точках среды, где

2πх / λ = ± mπ (m = 0, 1, 2, …),

амплитуда колебаний достигает максимального значения равного 2А. В точках среды, где

2πх / λ = ± (m + 1/2) π (m = 0, 1, 2, …),

амплитуда колебаний превращается в нуль. Точки, в которых амплитуда колебаний максимальна А_ст = 2А), называются пучностями стоячей волны, а точки, в которых амплитуда колебаний равна нулю (А_ст = 0), называют узлами стоячей волны. Точки среды, находящиеся в узлах, колебаний не совершают.

Из предыдущего выражений получим соответственно координаты пучностей и узлов:

(m=0, 1, 2, …),

(m=0, 1, 2, …) (3.9)

Примеры решения задач.

Задача1.Материальная точка массой 5 г осуществляет гармонические колебания с частотой 0,5 Гц. Амплитуда колебаний равняется 3 см. Определить: 1) скорость точки в момент времени, если смещение точки от положения равновесия равняется 1,5 см, 2) максимальную силу, которая действует на точку, 3) полную энергию колебаний.

Дано: кг Гц м м	Решение. А х1 -А 0 А х Рис.5.1.
υ - ? Fmax - ? Е - ?

Рис.5.1.

1)Кинематическое уравнение гармонического колебания мате-ріальної точки вдоль оси x имеет вид:

. (5.16)

Чтобы найти скорость, продиференцем это уравнения за временем:

. (5.17)

Чтобы выразить скорость через смещение, надо исключить из уравнений (5.16) и (5.17) время. Для этого подведем оба уравнения квадрат, разделим первое на A₂, второе на A₂ ² и добавим:

.

или с учетом (5.2):

Отсюда:

м/с.

Знак плюс отвечает случаю, если направление скорости совпадает с направлением оси , знак минус - если направление скорости совпадает с отрицательным направлением оси x.

2)Силу, который действует на точку, найдем по второму закону Ньютона

,где а - ускорение точки, численное значение которого получим, продифференцировав скорость за временем (так как точка двигается по прямой, нормальное ускорение равняется нулю)

или

Зная ускорения, найдем силу:

отсюда максимальное значение силы:

мН.

3) Полная энергия колеблющейся точки есть сумма кинетической и потенциальной энергий, вычисленных для любого момента времени. Вычислим полную энергию для момента времени, если кинетическая энергия достигает максимального значения. В этот момент потенциальная энергия равняется нулю. Итак,

.

Из выражения (5.17) найдем :

.

Итак,

Ответ: 1) м/с, 2) , 3) .

Задача 2.Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями

Найти уравнение траектории и построить её на чертеже.

Дано:	Решение 1) В исходных данных уравнение траектории задано в параметрическом виде (т.е. как х(t); y = y(t)). Чтобы найти уравнение траектории в координатной
у = у(х) - ?

форме (т.е. как у = у(х)), необходимо исключить время t. Для этого воспользуемся тригонометрической формулой . В данном случае , т.е.

или

или

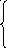(1)

(

2)

или вычитаем из уравнения (1) уравнение (2),

Рис.1

Получилось уравнение параболы, вершина которого находится в т.С (0;1), см. рис1.

Дано: l = 1,2 м Т = Тmin	Решение: 1) Период колебания физического маятника ,
X - ?

Задача 3.Физический маятник в виде тонкого прямого стержня длиной l = 120 см колеблется около горизонтальной оси, проходящей перпендикулярно стержню через точку, удаленную на некоторое расстояние а от центра масс стержня. При каком значении а период колебаний имеет наименьшее значение?

где J - момент инерции колеблющегося тела относительно оси колебаний (в данном случае т.О), Х – расстояние центра тяжести маятника от оси колебаний.

2) Момент инерции данного физического маятника (стержня) запишем с учетом теоремы Штейнера, как

Тогда период колебаний запишется как

(1)

3) Найдем экстремум функции Т = Т(х) (ф-ла 1). Для этого вычислим :

.

Решим уравнение = 0, т.е.

Отсюда . Подходит .

При х = 0, , а при значение .

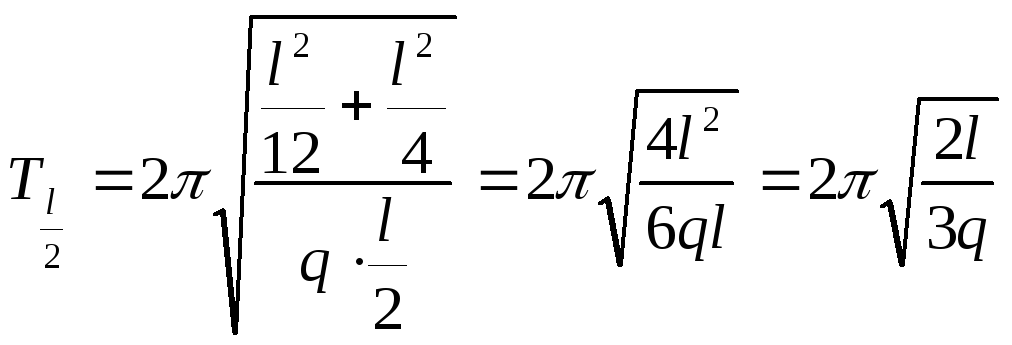Если при < , то тем самым докажем, что при найдено . Вычислим .

.

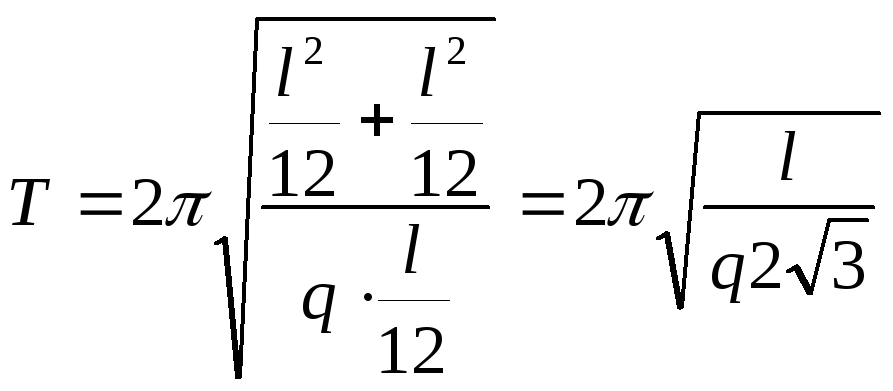Тогда < 1.

м.

Ответ.