9. Дифракция света. Основные формулы.

I. 3. Радиус зон Френеля

Радиус внешней границы m-й зоны Френеля для сферической волны (рис. 4.3):

(4.1)

для плоской волны :

(4.2)

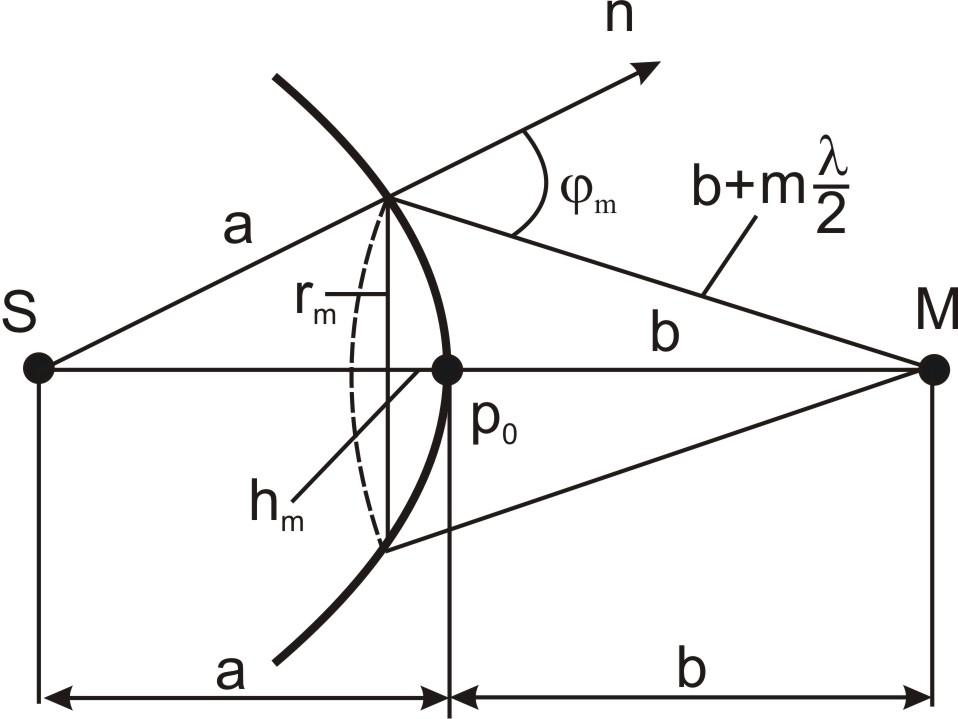
Рис. 4.3

I. 3. Условие максимумов и минимумов на одной щели.

Оптическая разность хода Δ между крайними лучами МС и ND , идущими от щели в произвольном направлении φ,

∆ = NF = α sin φ,

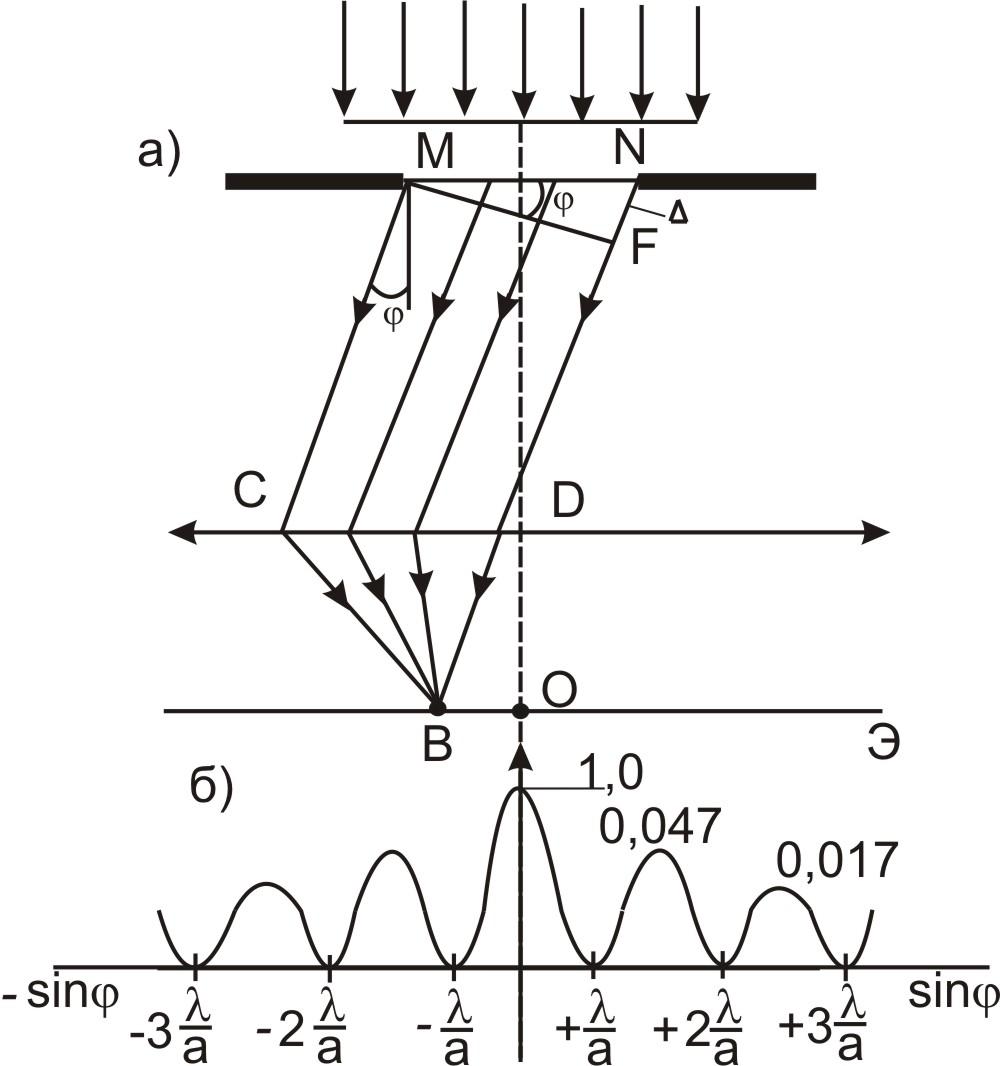
Рис. 4.8

Условие максимумов на одной щели:

(m = 1, 2, 3, …) (4.7)

Условие минимумов на одной щели:

(m=1, 2, 3, …) (4.6)

где а – ширина щели (МN),  - угол дифракции,  - длина волны, m - порядок максимума.

I. 3. Условие максимумов на дифракционной решетке.

Оптическая разность хода Δ между крайними лучами МВ и СВ, идущими от щели в произвольном направлении φ,

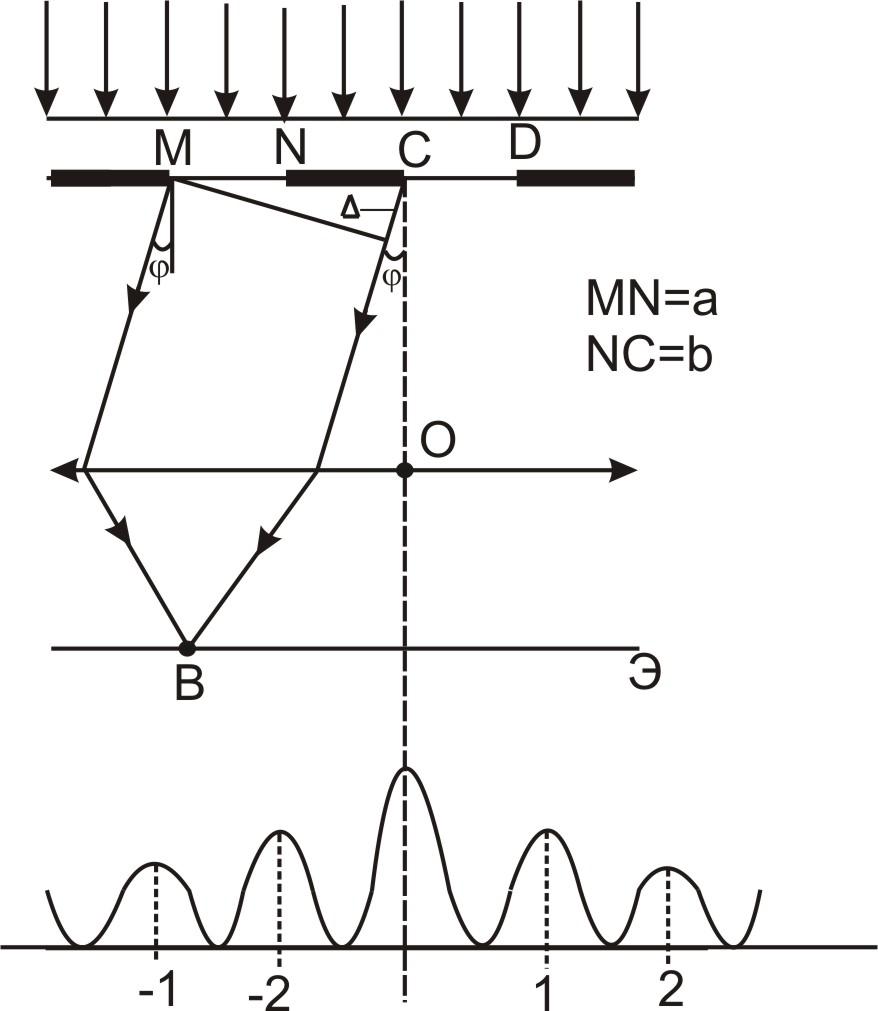
Рис.4.4.

(m =0, 1, 2, …) (4.5)

где d – период решетки,  - угол дифракции,  - длина волны, m - порядок максимума.

В случае N щелей между двумя главными максимумами располагается N – 1 дополнительных минимумов, разделенных вторичными максимумами, создающими весьма слабый фон.

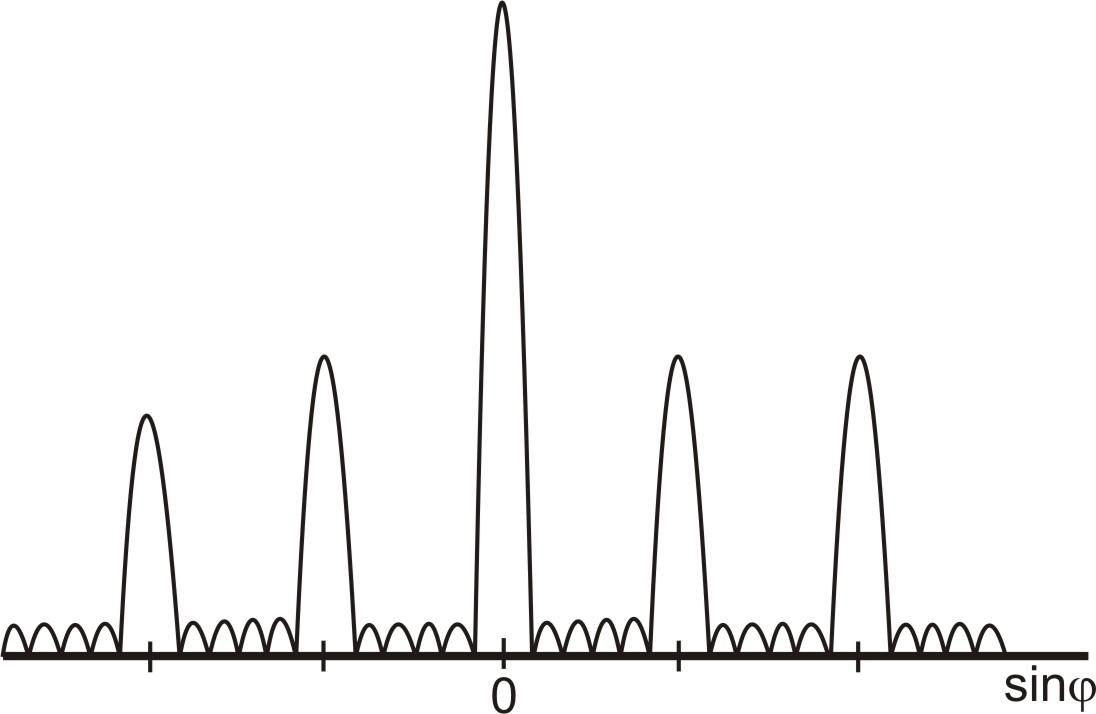
Рис. 4.5

II. 8. Формула Вульфа-Брэггов

Кристаллы можно представить в виде совокупности параллельных кристаллографических плоскостей (рис. 4.10), отстоящих друг от друга на расстоянии d. Пучок параллельных монохроматических лучей (1, 2) падает под углом скольжения θ (угол между направлением падающих лучей и кристаллографической плоскостью) и возбуждает атомы кристаллической решетки, которые становятся источниками когерентных вторичных волн 1^' и 2^', интерферирующих между собой, подобно вторичным волнам, от щелей дифракционной решетки. Максимумы интенсивности (дифракционные максимумы) наблюдаются в тех направлениях, в которых все отраженные атомами плоскостями волны будут находиться в одинаковой фазе. Эти направления удовлетворяют формуле Вульфа – Брэггов

, (m=1, 2, 3, …), (4.9)

Рис. 4.10

II. 10. Разрешающая способность дифракционной решетки.

Разрешающей способностью спектрального прибора называют безразмерную величину

, (4.10)

где - абсолютное значение минимальной разности длин волн двух соседних спектральных линий, при которых эти линии регистрируются раздельно.

Пусть максимум m-го порядка для длины волны λ₂ наблюдается под углом φ, т.е., d sin φ = m λ₂. При переходе от максимума к соседнему минимуму разность хода меняется на λ/N, где N – число щелей решетки. Следовательно, минимум λ₁, наблюдаемый под углом φ_min, удовлетворяет условию d sin φ_min = mλ₁ + λ₁/N. По критерию Рэлея, φ = φ_minт.е. mλ₂ = mλ₁ + λ₁/N или λ₂/(λ₂ – λ₁) = mN. Так как λ₁ и λ₂ близки между собой, т.е. λ₂ - λ₁ = δλ,

R_{диф. реш} =mN (4.11)

где m – порядок спектра; N – число щелей.