- •В.В. Бібик, т.М. Гричановська, л.В.Однодворець, н.І.Шумакова фізика твердого тіла
- •Isbn © Бібик в.В., Гричановська т.М.,
- •Однодворець л.В., Шумакова н.І., 2010
- •Передмова редактора
- •Розділ 1 будова твердих тіл
- •Операції і елементи симетрії
- •1.2. Елементарні комірки і решітки Браве
- •1.3. Обчислення періоду решітки
- •1.4. Кристалографічні символи
- •1.5 Типи зв’язків у твердих тілах
- •1.6 Анізотропія кристалів
- •1.7 Дефекти кристалів
- •Питання і завдання до розділу 1
- •Розділ 2 динаміка кристалічної решітки
- •2.1 Елементи теорії пружності
- •2.2 Уявлення про нормальні коливання решітки
- •2.3 Елементи квантової теорії пружних хвиль у кристалі
- •2.4 Спектр нормальних коливань решітки
- •Теплоємність кристалів при низьких і високих температурах
- •Питання і завдання до розділу 2
- •Розділ 3. Зонна теорія твердих тіл
- •3.1. Рівняння Шредінгера для кристала
- •3.2. Функція Блоха, теорема Блоха
- •3.3 Енергетичні зони кристала
- •3.4 Енергетичний спектр електронів у кристалі. Модель Кроніга-Пенні
- •3.5 Ефективна маса електрона в кристалі. Ізоенергетичні поверхні
- •Питання і завдання до розділу 3
- •Розділ 4 електронна теорія металів
- •4.1 Класична електронна теорія металів
- •4.2 Квантова статистика електронів у металі
- •4.3 Вироджений електронний фермі-газ у металах і його теплоємність
- •4.4 Кінетичне рівняння Больцмана для електрона в кристалі. Електропровідність металів
- •Питання і завдання до розділу 4
- •Розділ 5 електронна теорія напівпровідників
- •5.1. Загальна характеристика напівпровідників
- •5.2 Статистика електронів у напівпровідниках із власною провідністю
- •Елементи статистики електронів у домішкових напівпровідниках
- •5.4. Провідність напівпровідників
- •5.5 Ефект Холла у напівпровідниках
- •Питання і завдання до розділу 5
- •Електронна теорія магнетиків
- •6.1 Класифікація магнетиків
- •6.2. Діамагнетизм та парамагнетизм
- •6.3. Феромагнетизм, антиферомагнетизм, феримагнетизм
- •6.4 Феноменологічний опис феро- та антиферо-магнетизму
- •6.5. Взаємодії в упорядкованих магнетиках. Спінові хвилі
- •6.6. Елементи теорії Ландау. Процеси перемагнічування
- •Питання і завдання до розділу 6
- •Розділ 7 фазові переходи
- •7.1. Умови рівноваги фаз
- •7.2. Класифікація фазових переходів
- •7.3. Елементи теорії Ландау для фазових переходів другого роду
- •Питання і завдання до розділу 7
- •Задача 2
- •Розв’язання
- •Задача 9
- •Розв’язання
- •Задача 12
- •Розв’язання
- •Задача 13
- •Розв’язання
- •Додаток б (обов’язковий) Задачі для самостійного розв’язування
- •Додаток в (обов’язковий) Варіанти індивідуальних завдань
- •Список літератури
- •Фізика твердого тіла
Питання і завдання до розділу 7
-
Назвіть основний принцип формування структури кристалів.
-
Дайте означення фази речовини і фазового переходу.
-
Сформулюйте і виведіть умову рівноваги двох фаз.
-
Назвіть ознаки фазового переходу першого роду та наведіть приклади відповідних процесів.
-
Поясніть, яке явище називають температурним гістерезисом.
-
Запишіть формулу Клапейрона-Клаузіуса та поясніть, які процеси вона визначає.
-
Назвіть ознаки фазового переходу другого роду та наведіть приклади відповідних процесів.
-
Сформулюйте основні положення і висновки теорії фазових переходів другого роду, створеної Л. Ландау.
Додаток А
(обов’язковий)
Приклади розв’язування задач
Задача 1
Написати індекси напрямку прямої, яка проходить через вузли [[100]] та [[001]] примітивної кубічної решітки [22].
Розв’язання
Зобразимо примітивну кубічну решітку, відмітимо на ній вузли з індексами [[100]] та [[001]] і проведемо через ці вузли пряму (Рис. А.1, а).
Якби пряма проходила через початок координат, то індекси її напрямку збіглися б з індексами вузла, найближчого до початку координат із вузлів, через які проходить пряма.
Якщо
перенести початок координат у вузол
[[100]]
(Рис. А.1, б), то вузол, який лежить на тій
самій прямій і найближчий до вибраного
початку координат, буде мати індекси
[[![]() 01]],
а шуканий напрямок у цьому випадку
визначається індексами [
01]],
а шуканий напрямок у цьому випадку
визначається індексами [![]() 01].
01].
Якщо
ж початок координат перенести у вузол
[[001]]
(Рис. А.1, в) , то відповідно індекси
напрямку будуть [10![]() ].
Отже, індекси шуканого напрямку в
кристалі [
].
Отже, індекси шуканого напрямку в
кристалі [![]() 01]
або [10
01]
або [10![]() ].
].
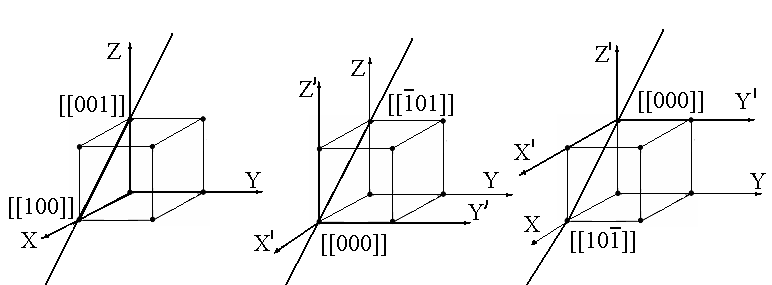
а б в
Рисунок А.1 - Пояснення до задачі 1
Не завжди можна легко визначити, як змінюються індекси вузлів при перенесенні початку координат. Тому розглянемо аналітичний метод розв’язання задачі.
Напишемо у загальному вигляді рівняння прямої, яка проходить через дві точки у просторі, з індексами вузлів [[m1n1p1]] та [[m2n2p2]]:
![]() .
(1)
.
(1)
Величини, які утворюються у знаменнику, пропорційні напрямним косинусам прямої. Оскільки ці величини - цілі числа, то вони і будуть індексами напрямку.
Підставимо у знаменник виразу (1) значення індексів вузлів m1=1, n1=0, p1=0 та m2=0, n 2=0, p2=1 і отримаємо:
m2 – m1 =0–1=–1,
n2 – n1 =0–0= 0,
p2 – p1 =1–0=1.
Таким
чином, шукані індекси напрямку [![]() 01].
01].
Відповідь:
індекси напрямку [![]() 01].
01].
Задача 2
Написати індекси Міллера для площини, яка має вузли з індексами [[200]], [[010]] [[001]]. Решітка примітивна, кубічна [22].
Розв’язання
Можливі два способи розв’язання задачі. Перший спосіб застосовується тоді, коли вузли, що належать площині, одночасно лежать і на осях координат (тобто відомі відрізки, відсічені площиною на осях координат).
У
даному випадку вузли, лежать на осях
координат, отже, відрізки (в одиницях
сталої решітки), які відсікаються на
осях координат цією площиною, відповідно
будуть 2, 1, 1 (Рис. А.2). У відповідності
до загального правила знаходження
індексів Міллера запишемо зворотні
значення отриманих чисел
![]() та зведемо їх до найменшого спільного
знаменника. Отримана сукупність значень
у чисельниках дробів і є шуканими
індексами Міллера (122).
та зведемо їх до найменшого спільного
знаменника. Отримана сукупність значень
у чисельниках дробів і є шуканими
індексами Міллера (122).
|
|
Рисунок А.2 - Схематичне зображення кристалографічної площини
|
Другий спосіб (аналітичний) особливо зручний тоді, коли відомі вузли не лежать на осях координат. Цей спосіб є загальним і застосовується у всіх випадках.
Відомо, що індекси Міллера дорівнюють найменшим цілочисловим коефіцієнтам при змінних у загальному рівнянні площини. Тому розв’язання задачі з визначення індексів Міллера зводиться до знаходження рівняння площини.
Рівняння площини, що проходить через три точки з координатами [[m1n1p1]], [[m2n2p2]], [[m3n3p3]], задається визначником третього порядку
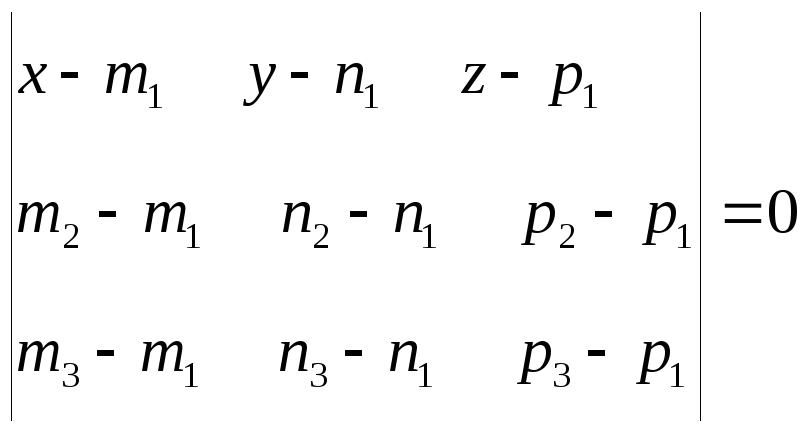 .
.
У нашому випадку: m1=2, n1=0, p1=0; m2=0, n2=1, p2=0; m3=0, n3=0, p3=0. Підставляючи значення індексів вузлів у визначник, отримаємо
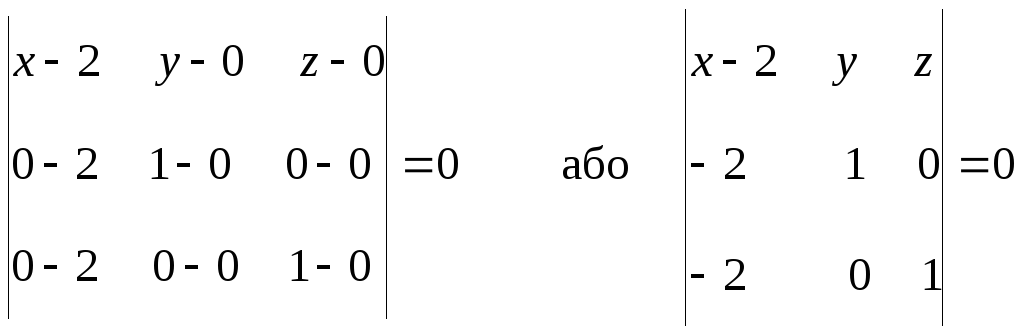 .
.
Розкладемо цей визначник за елементами першого рядка
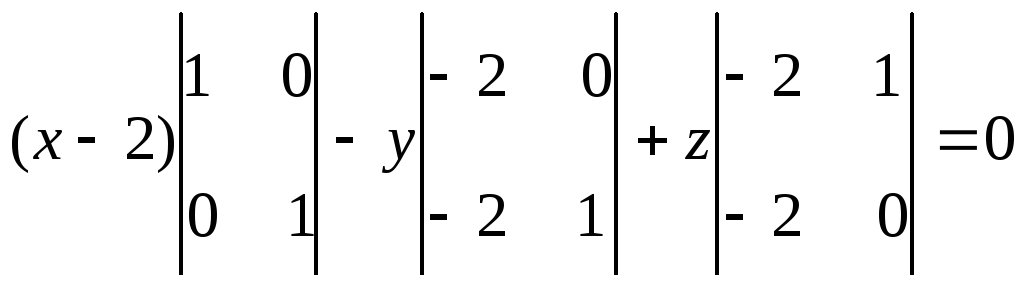 .
.
Розкривши визначник другого порядку, отримаємо
(x-2)(+1)-y(-2)+z(+2)=0 або x+2y+2z=2.
Коефіцієнти при x, y, z і є індексами Міллера (122).
Ці значення індексів, як і слід було очікувати, збігаються із значеннями, отриманими першим способом.
Відповідь: індекси Міллера (122).
Задача 3
Визначити
відносну атомну масу кристала, якщо
відомо, що відстань d
між найближчими сусідніми атомами
дорівнює 0,304 нм. Густина ρ
кристала дорівнює 534![]() .
Решітка об’ємноцентрована кубічної
сингонії.
.
Решітка об’ємноцентрована кубічної
сингонії.
Розв’язання
Маса
кристала
![]() ,
де
,
де
![]() об’єм
кристала (
об’єм
кристала (![]() -
об’єм однієї елементарної комірки),
-
об’єм однієї елементарної комірки),
![]() число
елементарних комірок у кристалі масою
m;
число
елементарних комірок у кристалі масою
m;
![]() =
=![]() .10-3
-
молярна маса, виміряна в кг/моль; n
=2 - кількість атомів в елементарній
комірці ОЦК-решітки.
.10-3
-
молярна маса, виміряна в кг/моль; n
=2 - кількість атомів в елементарній
комірці ОЦК-решітки.
Таким чином, отримуємо співвідношення
![]() ,
,
звідки
знаходимо
![]() ;
;
![]() .
.
За таблицею Менделєєва знаходимо, що це літій.
Відповідь:![]() =6,95.
=6,95.
Задача 4
Знайти сталу решітки (а) і відстань (d) між найближчими сусідніми атомами кристала:
1) алюмінію (ГЦК - решітка);
2) вольфраму (ОЦК - решітка).
Розв’язання
Густину
кристалів
![]() можна знайти як відношення маси
елементарної комірки m
до її об’єму V:
можна знайти як відношення маси
елементарної комірки m
до її об’єму V:
![]()
де
![]() -
маса одного атома; n-
кількість атомів в одній елементарній
комірці (для ГЦК – решітки n=4,
для ОЦК - решітки n=2);
а-
параметр решітки (a=d
-
маса одного атома; n-
кількість атомів в одній елементарній
комірці (для ГЦК – решітки n=4,
для ОЦК - решітки n=2);
а-
параметр решітки (a=d![]() для ГЦК-решітки,
для ГЦК-решітки,
![]() для
ОЦК-решітки);
для
ОЦК-решітки);
![]() -
молярна маса речовини кристала. Таким
чином, виконуємо розрахунки за формулою
-
молярна маса речовини кристала. Таким
чином, виконуємо розрахунки за формулою
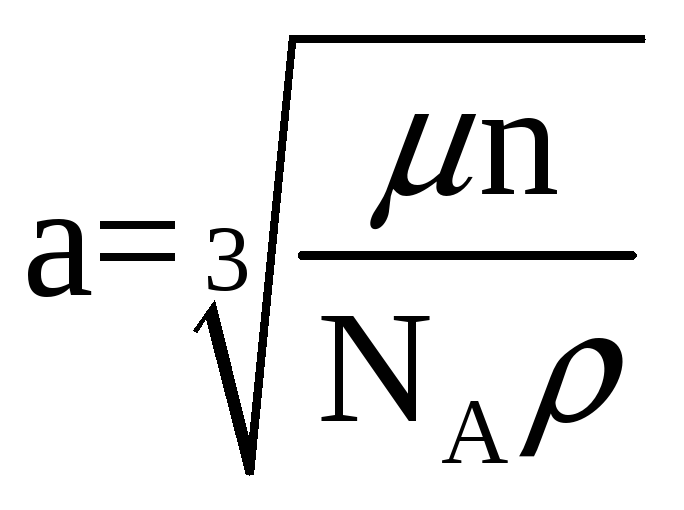 .
.
-
Для А1
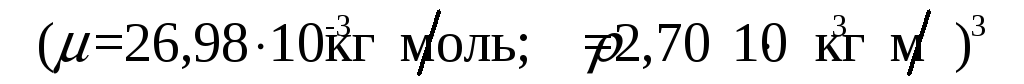
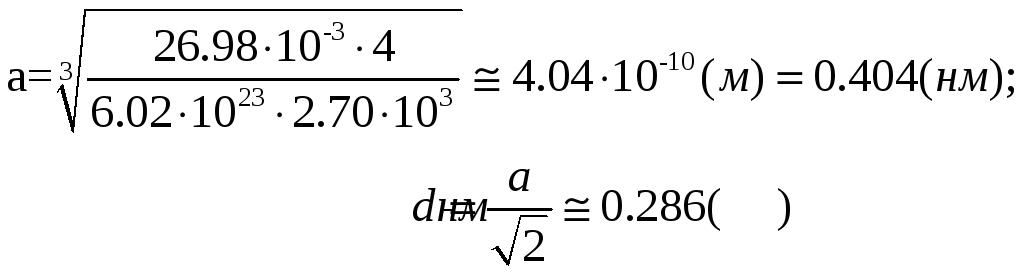
-
Для W
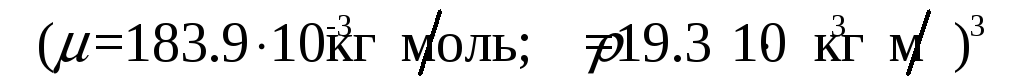
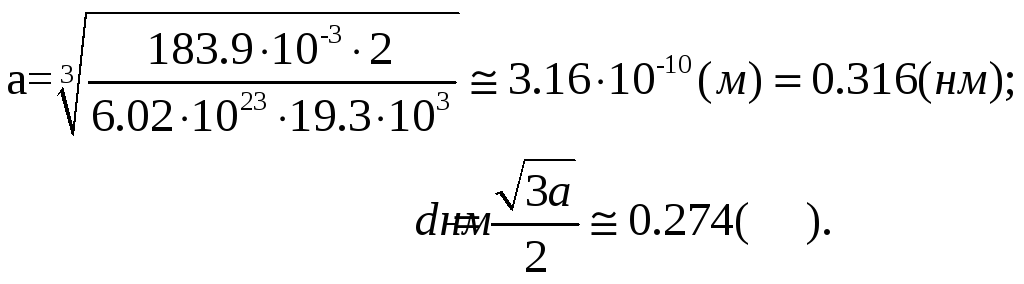
Відповідь: 1) а=0,404нм, d=0,286нм; 2) а=0,316нм, d=0,274нм.
Задача 5
Обчислити максимальну
частоту
![]() Дебая, якщо відомо, що молярна теплоємність
Дебая, якщо відомо, що молярна теплоємність
![]() срібла при Т=20K
дорівнює 1,7Дж/(моль
К).
срібла при Т=20K
дорівнює 1,7Дж/(моль
К).
Розв’язання
Частота Дебая зв’язана
з температурою Дебая
![]() таким співвідношенням:
таким співвідношенням:
![]() .
.
Відповідно до теорії теплоємності кристалів Дебая в області низьких температур
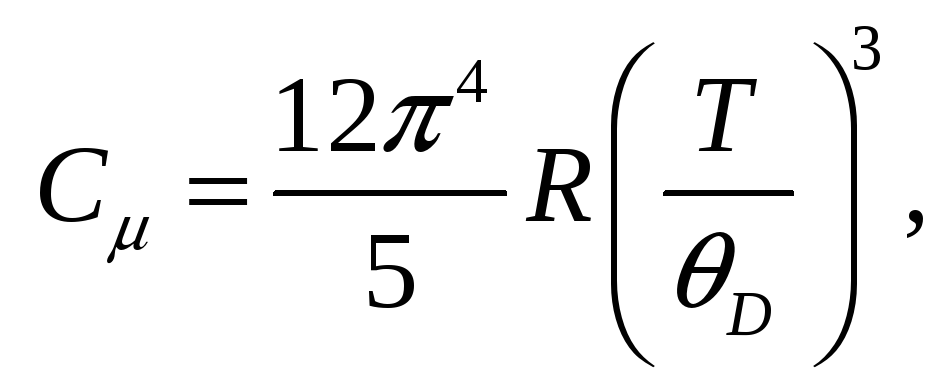
тоді
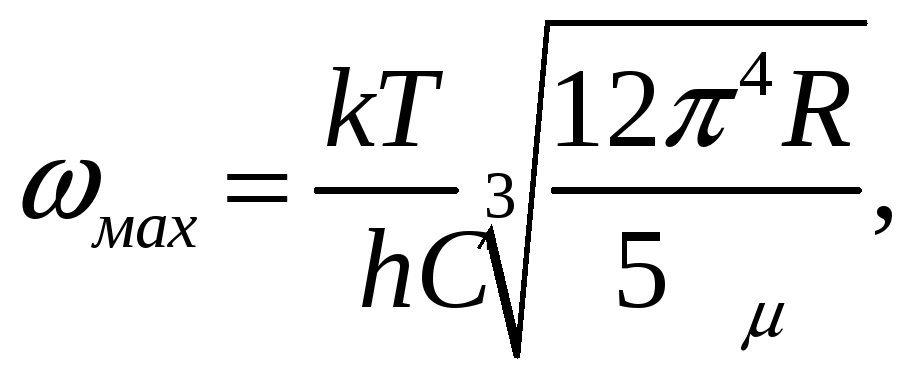
![]()
Відповідь:
![]() .
.
Задача 6
Для нагрівання срібла
масою m=10г
від 10К до 20К було витрачено
![]() Дж
тепла. Визначити характеристичну
температуру
Дж
тепла. Визначити характеристичну
температуру![]() Дебая срібла. Вважати
Дебая срібла. Вважати
![]() .
.
Розв’язання
Частота Дебая зв’язана
з температурою Дебая
![]() співвідношенням
співвідношенням
![]() .
.
Відповідно до теорії теплоємності Дебая кристалів в області низьких температур
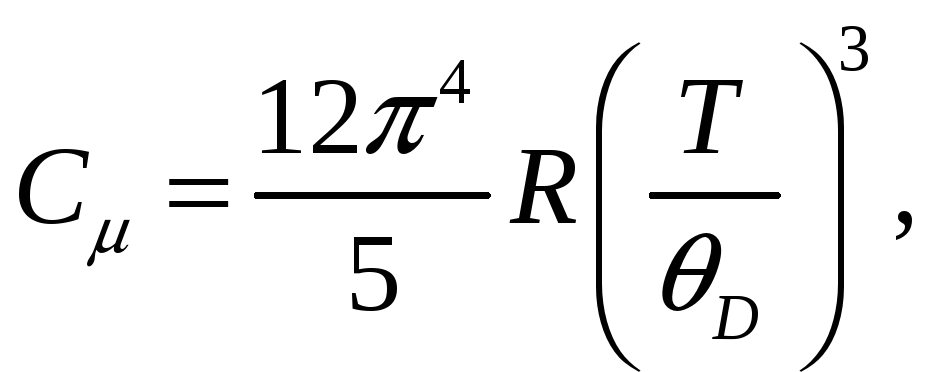
тоді
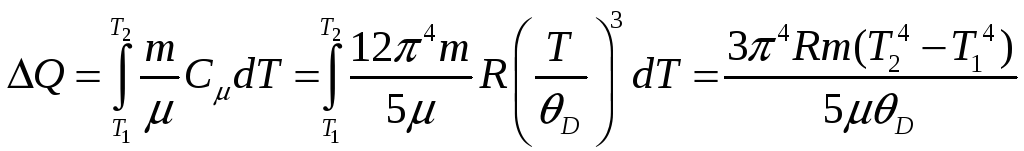 ,
,
де
![]() кг/моль
– молярна маса срібла,
кг/моль
– молярна маса срібла,
звідки знаходимо
![]() .
.
Відповідь:
![]() .
.
Задача 7
Період d
решітки одновимірного кристала дорівнює
0,3 нм. Знайти максимальну енергію
![]() фононів, якщо усереднена швидкість
звуку в кристалі v=5
км/с.
фононів, якщо усереднена швидкість
звуку в кристалі v=5
км/с.
Розв’язання
Максимальна енергія фонона визначається за формулою
![]() ,
,
де
![]() – максимально можлива частота коливань
у кристалі;
– максимально можлива частота коливань
у кристалі;
![]() – мінімальна довжина хвилі, яка може
реалізуватись у кристалі.
– мінімальна довжина хвилі, яка може
реалізуватись у кристалі.
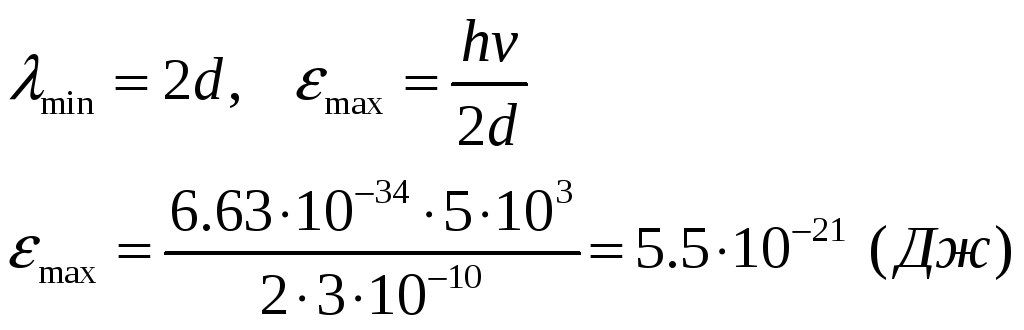
Відповідь:
![]() .
.
Задача 8
Визначити усереднену
швидкість звуку у кристалі, характеристична
температура
![]() якого 300К. Міжатомна відстань d
у кристалі дорівнює 0,25 нм.
якого 300К. Міжатомна відстань d
у кристалі дорівнює 0,25 нм.
Розв’язання
Відповідно до визначення
![]()
де
![]() –
максимально можлива частота коливань
у кристалі;
–
максимально можлива частота коливань
у кристалі;
![]() – мінімальна довжина хвилі, яка може
реалізуватись у кристалі ( див. рис.
2.1).
– мінімальна довжина хвилі, яка може
реалізуватись у кристалі ( див. рис.
2.1).
Таким чином,
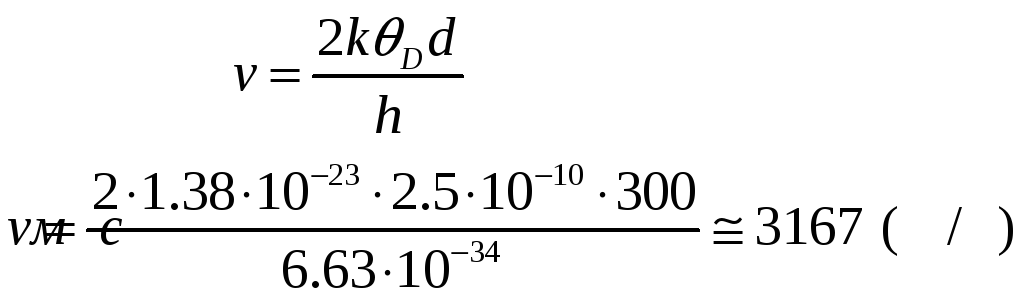
Відповідь:
![]() .
.