0. 7.2. Класифікація фазових переходів

Згідно з класифікацією Еренфеста розрізняють фазові переходи першого та другого родів. До фазових переходів першого роду відносять переходи, за яких стрибком змінюються величини, що визначаються як перші похідні термодинамічного потенціалу за температурою та тиском.

До них, зокрема, належать

, (7.9)

або в розрахунку на одну молекулу

. (7.10)

З останнього співвідношення видно, що похідні не дорівнюють нулю, отже, при фазових переходах першого роду ентропія та об'єм повинні змінюватись стрибком. Оскільки термодинамічний потенціал (у розрахунку на одну частинку)

при фазових переходах першого роду змінюється неперевно то, очевидно, що стрибком змінюється енергія U. Стрибкоподібна зміна ентропії при фазових переходах першого роду зумовлює появу теплоти переходу, яка виділяється або поглинається під час переходу. Кристалічна структура при фазових переходах першого роду і симетрія кристала в точці фазового переходу також змінюються стрибком. При цьому симетрія кристала може змінюватись довільно, отже, обидві фази можуть і не мати спільних елементів симетрії.

З умовою неперервної зміни термодинамічного потенціалу в області фазового переходу першого роду пов'язана принципова можливість перегріву або переохолодження фаз.

Продиференціювавши обидві сторони співвідношення (7.8), можна отримати формулу Клапейрона-Клаузіуса

, (7.11)

де Q – кількість теплоти, що поглинається (виділяється) при фазовому переході першого роду.

Формула Клапейрона-Клаузіуса визначає зміну тиску в системі зі зміною температури або зміну температури фазового переходу між двома фазами зі зміною тиску.

Перебіг фазового переходу першого роду зумовлений процесом виникнення зародка, тому він супроводжується температурним гістерезисом. Під температурним гістерезисом розуміють незбіг температури фазового переходу при нагріванні та охолодженні. Фізичні причини температурного гістерезису є, очевидно, такими, які приводять до утворення метастабільного стану труднощі утворення зародків нової фази. Типовим прикладом цих процесів можуть служити процеси кристалізації та плавлення.

Фазові переходи другого роду характеризуються не тільки неперервністю термодинамічного потенціалу, але і його перших похідних за температурою та тиском, тобто неперервністю ентропії та об'єму. При фазових переходах другого роду стрибком змінюються другі похідні д²G/др² та д²G/дТ², через які виражені теплоємність, коефіцієнт теплового розширення та стисливість:

, (7.12)

, (7.13)

. (7.14)

Оскільки при фазових переходах другого роду ентропія не змінюється, то згідно з (7.11) теплота переходу дорівнює нулю. Кристалічна структура при фазових переходах другого роду також змінюється неперервно.

При фазових переходах другого роду температурний гістерезис не спостерігається.

При фазових переходах другого роду структура змінюється не стрибком, а - неперервно. Як і у попередньому випадку, симетрія кристала в точці фазового переходу змінюється стрибком. Однак існує відмінність у характері зміни симетрії при фазових переходах першого та другого родів. При фазових переходах роду симетрія однієї із фаз є підгрупою симетрії іншої. Більш симетричною переважно є високотемпературна фаза, а менш симетричною -низькотемпературна фаза.

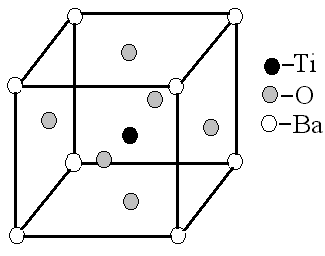
Розглядаючи характер зміни кристалічної структури при фазових переходах, можна виділити фазові переходи типу зміщення та типу порядок-непорядок. Прикладом фазового переходу типу зміщення є фазовий перехід у ВаТіО₃. При температурах, вищих від температури Кюрі (Т_к=393К), титанат барію має кубічну ґратку, в якій атоми барію знаходяться при вершинах куба, атоми титану - в центрі куба, а атоми кисню - у центрі граней, утворюючи октаедричне оточення навколо центрального іона (рис. 7.1). У разі такого розміщення геометричний центр від'ємних зарядів збігається з положенням атома титану, отже, результуючий дипольний момент решітки дорівнює нулю (кристал перебуває у параелектричній фазі). При температурі Кюрі атоми титану та кисню стрибком зміщуються відносно атомів барію в напрямі одного із ребер, і решітка із кубічної перетворюється у тетрагональну. При цьому виникає дипольний момент, напрям якого збігається з напрямом зміщення атомів.

Прикладом фазового переходу типу порядок - непорядок може бути сегнетоелектричний фазовий перехід, зумовлений впорядкуванням водневих зв'язків. У цьому випадку різниця між параелектричною та сегнетоелектричною фазами полягає в тому, що в параелектричній фазі ймовірності різних орієнтацій водневих зв'язків є однаковими, а в сегне-тоелектричній - різними.

Рисунок 7.1 - Кристалічна структура ВаТіО3

В однокомпонентних кристалах зміна термодинамічних функцій з температурою визначається перш за все коливаннями атомів або фононною складовою. Фазовий перехід з однієї фази у іншу можливий за умови, коли частоти коливань у другій фазі є меншими, ніж у першій. Отже, фаза 2 повинна бути менш жорсткою, ніж фаза 1. Для точного вивчення питання переходу потрібен аналіз реального фононного спектра. У такому випадку виявляється, що фазовий перехід зумовлюватиме різниця не усіх частот коливань, а тільки певних гілок. Вважається, що в разі такого фазового переходу відбувається пом 'якшення певних мод коливань. Значна роль фононної складової властива також деяким сплавам та багатьом сегнетоелектрикам.